Fluida dinamis merupakan salah satu materi fisika yang dipelajari di kelas 11 semester 1, oleh karena itu disini saya mencoba untuk membuat latihan soal materi Fluida dinamis lengkap dengan pembahasannya secara terperinci, bisa dijadikan latihan untuk para siswa agar lebih memahami materi fluida dinamis atau referensi oleh guru dalam membuat soal ulangan. Soal yang disajikan memiliki banyak tipe soal yang diambil dari soal-soal ujian masuk atau UN sehingga cocok untuk dibuat belajar menjelang ulangan harian atau akan mengikuti tes. Selamat menikmati
Soal nomor 1
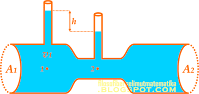
Suatu zat cair dialirkan melalui pipa seperti tampak pada gambar di samping. Jika luas penampang A1 = 10 cm2, A2 = 4 cm2, dan laju zat cair v2 = 4 m/s, besar v1 adalah ....
A. 0,6 m/s
B. 1,0 m/s
C. 1,6 m/s
D. 2,0 m/s
E. 2,4 m/s
Kunci jawaban: "C"
Soal nomor 2
Cairan mengalir melalui pipa berdiameter 5 cm pada kelajuan 4 m/s. ada penyempitan dengan diameter 2 cm dalam saluran pipa. Kecepatan cairan dalam penyempitan itu adalah ....
A. 0,64 m/s
B. 1,6 m/s
C. 10 m/s
D. 25 m/s
E. 50 m/s
Kunci jawaban: "D"
Soal nomor 3
Sebuah pipa dengan luas penampang 616 cm2 dipasangi keran berjari – jari 3,5 cm di salah satu ujungnya. Jika kecepatan zat cair di pipa adalah 0,5 m/s, dalam waktu 5 menit volume zat cair yang keluar dari keran adalah .... m3
A. 10,2
B. 9,24
C. 8,29
D. 6,72
E. 5,2
Kunci jawaban: "B"
Soal nomor 4
Seorang anak mengisi sebuah ember yang memiliki volume 0,019 m3 dengan menggunakan keran yang memiliki diameter 0,008 m. apabila air keluar dari keran dengan laju tetap 0,61 m/s. maka waktu yang diperlukan untuk memenuhi ember tersebut adalah ....
A. 5,16 menit
B. 10,55 menit
C. 15,45 menit
D. 17,90 menit
E. 20,66 menit
Kunci jawaban: "B"
Soal nomor 5
Pada gambar di samping, G adalah generator 1.000 W yang digerakkan dengan kincir air. generator hanya menerima energi sebesar 80% dari energi air. jika generator dapat bekerja normal, debit air yang sampai ke kincir adalah ....
A. 12,5 L/s
B. 22,0 L/s
C. 27,5 L/s
D. 125 L/s
E. 150 L/s
Kunci jawaban: "A"
Soal nomor 6
Sebuah pipa air memiliki ujung-ujung yang berbeda luas penampangnya. Luas penampang ujung b setengah kali luas penampang ujung a. Air masuk melalui ujung a sebanyak 1 liter/s dengan kelajuan 10 cm/s. jika di tengah pipa terdapat kebocoran sebanyak 50 cc tiap sekon, air keluar dari ujung b dengan kelajuan sebesar ....
A. 20 cm/s
B. 19 cm/s
C. 18 cm/s
D. 17 cm/s
E. 16 cm/s
Kunci jawaban: "B"
Soal nomor 7
Sebuah cairan mengalir melewati pipa mendatar yang luas penampangnya makin mengecil. Pada ujung pipa yang besar air memiliki kelajuan 3,0 m/s dan kelajuan air di ujung pipa kecil adalah 5,0 m/s. jika beda tekanan antara kedua ujung pipa adalah 2,8 kPa, maka kerapatan cairan yang mengalir dalam pipa adalah .... kg/m3
A. 350
B. 450
C. 550
D. 650
E. 750
Kunci jawaban: "A"
Soal nomor 8
Suatu fluida tak termampatkan dengan massa jenis ρ mengalir melalui suatu pipa mendatar dengan jari-jari r, kemudian melewati suatu penyempitan dengan jari-jari r/2. Jika fluida memiliki tekanan P0 dan kecepatan v0 sebelum penyempitan, tekanan dalam bagian yang menyempit adalah ....
A. P0 – 15/2 ρv02
B. P0 – 3/2 ρv02
C. P0/4
D. P0 – 3/4 ρv02
E. P0 – 15/4 ρv02
Kunci jawaban: "A"
Soal nomor 9
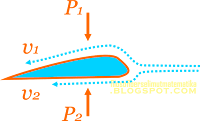
Perhatikan gambar alat penyemprot nyamuk pada gambar di bawah ini!
Ketika batang penghisap M ditekan, udara dipaksa keluar dari tabung pompa dengan kecepatan v melalui lubang pada ujungnya. P menyatakan tekanan dan v menyatakan kecepatan alir cairan obat nyamuk, maka pernyataan yang benar dari prinsip kerja penyemprot nyamuk tersebut adalah ....
A. P1 < P2, maka v1 < v2
B. P1 > P2, maka v1 < v2
C. P1 < P2, maka v1 > v2
D. P1 > P2, maka v1 > v2
E. P1 = P2, maka v1 = v2
Kunci jawaban: "B"
Soal nomor 10
perhatikan gambar berikut.
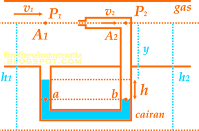
Sebuah semprotan nyamuk tersusun atas pipa vertikal yang tercelup dalam cairan antinyamuk dengan massa jenis ρ dan pipa horizontal yang terhubung dengan piston. Panjang bagian pipa vertikal yang berada di atas cairan adalah l dengan luas penampang a. diperlukan kecepatan minimum aliran udara yang keluar dari pipa horizontal sebesar v agar cairan antinyamuk dapat keluar dari pipa vertikal. Jika cairan antinyamuk diganti dengan merek lain dengan massa jenis ρ’ = 1,2ρ , maka besar kecepatan minimum aliran udara yang diperlukan adalah ....
A. v’ = 5/6 v
B. v’ = v
C. v’ = √1,2 v
D. v’ = 1,2 v
E. v’ = 4 v
Kunci jawaban: "C"
Soal nomor 11
Gambar di bawah menunjukkan gambar penampang lintang sayap pesawat terbang yang luasnya 40 m2.
Gerak pesawat terbang menyebabkan kelajuan aliran udara di bagian atas sayap sebesar 250 m.s-2 dan kelajuan udara di bagian bawah sayap sebesar 200 m.s-2. Jika kerapatan udara adalah 1,2 kg.m-3, maka besar gaya angkat pesawat adalah ....
A. 10.800 N
B. 24.000 N
C. 98.500 N
D. 540.000 N
E. 608.000 N
Kunci jawaban: "D"
Soal nomor 12
perhatikan gambar berikut.
Suatu bejana diisi dengan zat cair sampai setinggi H. Pada dinding bejana terdapat lubang yang letaknya h di bawah permukaan zat cair. Zat cair akan jatuh ke permukaan sejauh ....
A. R = 2√h(H-h) dari dinding bejana
B. R = 2√gh dari dinding bejana
C. R = 2√(H-h) dari dinding bejana
D. R = √2gh dari dinding bejana
E. R = h(H-h) dari dinding bejana
Kunci jawaban: "A"
Soal nomor 13
perhatikan gambar berikut.
Suatu tangki terbuka diisi dengan air sampai setinggi 6 m. pada kedalaman 3 m di bawah permukaan air, terdapat kebocoran kecil di sisi tangki sehingga air menyemprot keluar dari lubang tersebut dan jatuh ke tanah sejauh R dari kaki tangki. Jarak R adalah ....
A. 2 m
B. 4 m
C. 6 m
D. 8 m
E. 10 m
Kunci jawaban: "C"
Soal nomor 14
Sebuah tangki dengan tinggi 2 m diletakkan di atas penyangga setinggi 8 m. pada permukaan samping bawah tangki terdapat lubang kecil. Kemudian tangki diisi penuh dengan air, dan air mengalir keluar melalui lubang kecil tersebut. jarak mendatar terjauh yang dapat dicapai aliran air yang keluar dari tangki adalah ....
A. 4 m
B. 6 m
C. 8 m
D. 10 m
E. 12 m
Kunci jawaban: "C"
Soal nomor 15
perhatikan gambar berikut.
Pada gambar di samping, air dalam tangki memancar ke luar melalui pancuran A yang membentuk sudut 300 terhadap tanah. Air yang keluar dari pancuran A akan jatuh ke tanah setelah selang waktu ....
A. 0,4 s
B. 0,6 s
C. 0,8 s
D. 1,0 s
E. 1,2 s
Kunci jawaban: "E"
Soal nomor 16
perhatikan gambar berikut.
Sebuah tangki air pada bawahnya terdapat lubang sehingga air memancar keluar membentuk sudut 600 seperti pada gambar. Jika jarak pancarnya x = 80√3 cm dan g = 10 m/s2, tinggi air (h) dalam tangki adalah ....
A. 20 cm
B. 80 cm
C. 80√3 cm
D. 128 cm
E. 160 cm
Kunci jawaban: "B"
Soal nomor 17
pada bak yang berisi air setinggi 1 m (diukur dari alasnya) terdapat kebocoran kecil pada dindingnya, yang jauhnya 20 cm dari permukaan air. sebuah lubang harus dibuat lagi pada jarak .... (diukur dari alasnya), sehingga tempat jatuhnya berimpit dengan kebocoran yang pertama.
A. 80 cm
B. 60 cm
C. 40 cm
D. 20 cm
E. 10 cm
Kunci jawaban: "D"
Soal nomor 18
Sebuah bak diisi air setinggi 20 m. di sisi bak dibuat 2 lubang yang masing-masing berjarak 2 m dari permukaan dan dasar tabung. Perbandingan jauh jarak air yang dipancarkan dari lubang-lubang tersebut adalah ....
A. 1 : 2
B. 1 : 1
C. 2 : 1
D. 1 : 3
E. 3 : 1
Kunci jawaban: "B"
Soal nomor 19
perhatikan gambar berikut.
Gambar di samping menunjukkan air mengalir dalam venturimeter dari pipa dengan luas penampang A1 ke A2 berturut – turut adalah 5 cm2 dan 3 cm2. Kelajuan air (v1) yang memasuki pipa venturimeter jika h = 20 cm adalah ....
A. 1,5 m/s
B. 3 m/s
C. 4 m/s
D. 5 m/s
E. 9 m/s
Kunci jawaban: "A"
Soal nomor 20
Air mengalir dalam sebuah venturimeter dengan manometer. Luas penampang pipa besar 100 cm2 dan luas penampang pipa kecil 20 cm2. Jika perbedaan tinggi raksa pada manometer 5 cm maka kecepatan air yang masuk melalui penampang kecil adalah .... (g = 10 m/s2, ρair = 1000 kg/m3, ρraksa = 13.600 kg/m3)
A. 2,28 m/s
B. 3,62 m/s
C. 4,52 m/s
D. 5,24 m/s
E. 6,77 m/s
Kunci jawaban: "B"
Soal nomor 21
perhatikan gambar berikut.
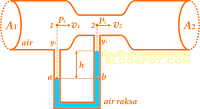
Kecepatan aliran gas dapat ditentukan dengan alat seperti pada gambar. Jika perbedaan tinggi raksa antara kedua kaki setinggi h dan massa jenis gas dan raksa berturut – turut ρ1 dan ρ2 , kecepatan aliran gas sebesar ....
A. v = √2 ρ2 gh / ρ1
B. v = √2 ρ1 gh / ρ2
C. v = √2 ρ2 ρ1 / gh
D. v = √2 ρ2 ρ1 gh
E. v = √2 ρ2 g / ρ1 h
Kunci jawaban: "A"
Soal nomor 22
Jika udara (ρudara = 1,29 kg/m3) dialirkan ke dalam pipa pitot dan perbedaan tinggi air raksa (ρraksa = 13600 kg/m3) pada manometer 3 cm maka kecepatan aliran udara tersebut adalah ... (g = 9,8 m/s2)
A. 53,76 m/s
B. 67,83 m/s
C. 78,73 m/s
D. 81,50 m/s
E. 83,71 m/s
Kunci jawaban: "C"
Soal nomor 23
perhatikan gambar berikut
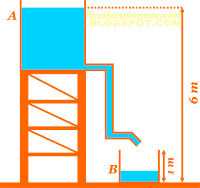
Pada gambar di atas, tinggi permukaan air pada bak A adalah 6 m dari lantai. Air dialirkan ke bak B melalui pipa. Tinggi ujung pipa dari lantai 1 meter. Penampang pipa 0,5 cm2. Debit air yang keluar lewat pipa adalah .... cm3/s
A. 100
B. 200
C. 300
D. 500
E. 1000
Kunci jawaban: "B"
Soal nomor 24
perhatikan gambar berikut.
Sebuah akuarium diisi air melalui sebuah keran yang debitnya 0,5 L/s, ternyata ada lubang yang luasnya 1,25 cm2 tepat di dasar kaca akuarium. Tinggi air maksimum (t) adalah .... (diameter lubang diabaikan terhadap t)
A. 20 cm
B. 40 cm
C. 60 cm
D. 80 cm
E. 100 cm
Kunci jawaban: "D"
Demikian latihan soal beserta pembahasannya tentang materi fisika fluida dinamis untuk kelas 11, sedikit yang bisa saya tuliskan ini semoga bisa memberikan manfaat bagi para pembaca sekalian. Jika berkenan bisa subscribed blog ini, atau memberikan kritik, saran dan pendapat di kolom komentar di bawah. Terima kasih












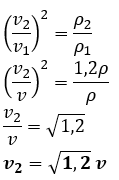






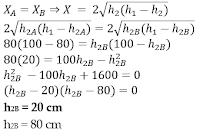
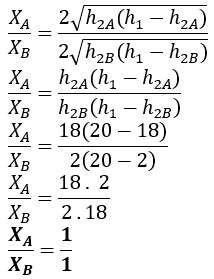



Tidak ada komentar:
Posting Komentar