Dalam materi tentang impuls momentum, kita mengenal sebuah istilah yang disebut dengan “koefisien restitusi” yang mana koefisien restitusi merupakan negatif perbandingan antara kecepatan relatif sesaat sesudah tumbukan dengan kecepatan relatif sesaat sebelum tumbukan pada tumbukan satu dimensi. Selain itu dapat pula di katakan bahwa koefisien restitusi menunjukkan “tingkat terpantul” benda setelah tumbukan, semakin besar koefisien restitusinya maka tingkat terpantulnya juga akan semakin besar jadi kedua benda setelah bertumbukan akan semakin terpantul atau kehilangan energi kinetiknya semakin kecil, sebaliknya semakin kecil koefisien restitusinya maka tingkat terpantul benda setelah tumbukan semakin kecil atau kehilangan energi kinetiknya akan semakin besar. nilai koefisien restitusi terbesar adalah 1 dan terkecil adalah 0, berdasarkan nilai koefisien restitusi ini kita dapat membedakan tumbukan menjadi tiga jenis yakni tumbukan lenting sempurna, tumbukan lenting sebagian, dan tumbukan tidak lenting sama sekali.
Tumbukan lenting sempurna memiliki nilai koefisien restitusi paling besar yaitu bernilai 1 (e = 1) hal ini menunjukkan benda setelah bertumbukan akan saling terpantul dengan maksimal dan tidak ada kehilangan energi kinetik sehingga pada tumbukan lenting sempurna berlaku hukum kekekalan energi kinetik, tumbukan lenting sebagian memiliki nilai koefisien restitusi yang bervariasi antara 0 sampai 1 (0 < e < 1) yang mana pengaruh besar kecilnya koefisien restitusi ini sudah di jelaskan di atas, sedangkan untuk tumbukan tidak lenting sama sekali memiliki nilai koefisien restitusi sama dengan 0 (e = 0) hal ini menunjukkan kedua benda setelah bertumbukan tidak akan terpantul, akan tetapi bergerak bersama – sama. untuk lebih memahami materi tentang tumbukan bisa di baca di sini.
Persamaan untuk koefisien restitusi dapat diturunkan dengan menggunakan konsep hukum kekekalan energi kinetik dan hukum kekekalan momentum, misalkan untuk dua benda A dan B yang masing – masing bergerak dengan kecepatan vA dan vB. keduanya bertumbukan secara lenting sempurna sehingga kecepatan keduanya menjadi v’A dan v’B, Kita dapat menganalisis fenomena di atas dengan menggunakan hukum kekekalan energi kinetik dan hukum kekekalan momentum.
Hukum kekekalan momentum
pA + pB = p’A + p’B
mA vA + mB vB = mA v’A + mB v’B
mA vA - mA v’A = mB v’B - mB vB
mA (vA - v’A) = mB (v’B - vB) ... (1)
Hukum kekekalan kekekalan energi kinetik
EKA + EKB = EK’A + EK’B
½ mA vA2 + ½ mB vB2 = ½ mA v’A2 + ½ mB v’B2
mA vA2 – mA v’A2 = mB v’B2 – mB vB2
mA (vA2 – v’A2) = mB (v’B2 – vB2) ... (2)
pers (2) di bagi dengan pers (1)
Angka “1” di atas menunjukkan nilai koefisien restitusi untuk tumbukan lenting sempurna, sehingga secara umum persamaan koefisien restitusi untuk tumbukan adalah sebagai berikut.
Ketika terjadi tumbukan tidak lenting sama sekali, kedua benda setelah bertumbukan tidak terpantul dan bergerak bersama – sama sehingga kecepatan keduanya setelah bertumbukan adalah sama (v’B = v’A), maka persamaan koefisien restitusinya dapat kita tulis.
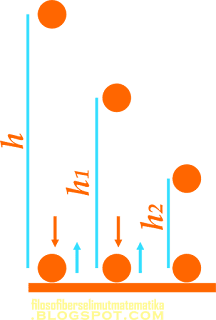
Kasus lain terkait dengan tumbukan dan koefisien restitusi selain pada dua benda yang bergerak horizontal di atas lantai adalah terkait dengan benda jatuh bebas ke lantai kemudian memantul. Misalkan sebuah bola bermassa m dijatuhkan tanpa kecepatan awal dari ketinggian h di atas lantai kemudian bola tersebut memantul beberapa kali seperti yang terlihat pada gambar di bawah ini
Pada saat bola jatuh bebas ke bawah berlaku hukum kekekalan energi sehingga kita dapat menentukan kecepatan benda sesaat sebelum bertumbukan dengan lantai seperti berikut
EP = EK
mgh = ½ mv2
gh = ½ v2
v2 = 2gh
v = √2gh ... (1)
dengan menggunakan cara yang sama seperti di atas, maka kita dapat menentukan hubungan antara kecepatan di dasar dengan ketinggian seperti berikut
v = √2gh
v1 = √2gh1
v2 = √2gh2
tumbukan terjadi antara bola dengan lantai (vL = 0), misalkan untuk tumbukan pertama sebuah bola yang jatuh dari ketinggian h memantul ke lantai hingga ketinggian h1 kemudian turun dan memantul hingga naik lagi hingga h2. Untuk pemantulan pertama kita dapat menentukan koefisien restitusinya yakni
Dengan cara yang sama untuk pantulan ke dua, kita dapat menentukan koefisien restitusinya adalah
Sehingga secara umum kita dapat menuliskan untuk gerak pantulan seperti ini berlaku








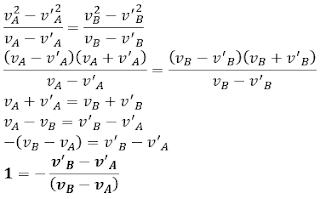
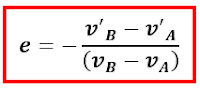
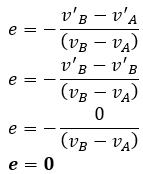


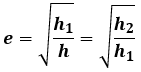

Tidak ada komentar:
Posting Komentar