Sebuah pegas ketika diberikan gaya (ditarik atau ditekan) akan kembali ke keadaan awal sesaat setelah gaya tersebut dihilangkan, hal yang sama juga berlaku untuk benda – benda yang bersifat elastis dan keadaan ini berlaku selama masih pada daerah elastis. Berdasarkan fenomena ini pada tahun 1976, seorang fisikawan bernama Robert Hooke mengemukakan hukum Hooke yang menyatakan bahwa “besarnya gaya yang diperlukan untuk meregangkan atau merapatkan sebuah pegas (gaya pegas) sama besar dengan besarnya gaya yang digunakan untuk meregangkan atau merapatkan pegas tersebut sejaub x”. Secara matematis hukum Hooke dapat ditulis
Fp = gaya pegas (N)
k = Konstanta pegas (N/m)
x = perubahan panjang pegas (m)
konstanta pegas merupakan suatu nilai yang bergantung dari jenis pegas yang digunakan, konstanta pegas ini berbanding terbalik dengan perubahan panjang pegas secara matematis dapat dijelaskan bahwa semakin besar konstanta pegas berbanding terbalik dengan perubahan panjang pegas. Hal ini juga mengandung makna bahwa semakin besar konstanta pegas maka benda semakin susah untuk berubah panjangnya atau dibutuhkan gaya yang lebih besar ketika ingin mengubah panjang pegas atau dapat pula dikatakan bahwa pegas tersebut semakin bersifat tidak elastis.
Tanda negatif menunjukkan bahwa gaya pegas arahnya selalu berlawanan dengan arah perpindahannya dari titik kesetimbangan, gaya pegas juga berfungsi untuk memulihkan panjang pegas kembali ke bentuk semula, oleh karena itu gaya pegas sering juga disebut dengan gaya pemulih.
Penting
Beberapa buku menuliskan rumus di atas tanpa tanda negatif (F = kΔx), hal ini dikarenakan gaya yang dimaksud pada persamaan tersebut bukan gaya pegas akan tetapi gaya luar yang dikerjakan pada pegas tersebut. Antara gaya pegas dan gaya luar yang dikerjakan ini memang besarnya sama akan tetapi arahnya berlawanan jadi jangan sampai bingung ketika melihat kedua rumus tersebut.
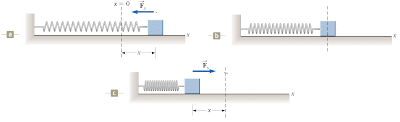
Gambar 6. Ilustrasi gaya pegas atau gaya pemulih
(sumber: Principle of Physics)
Perhatikan sebuah benda yang terhubung dengan sebuah pegas dengan salah satu ujungnya menempel di tembok, ketika balok bergerak ke kanan (x < 0) dan menarik pegas (gambar 6a) sehingga pegas menjadi lebih panjang maka arah gaya pegas akan ke kiri. Ketika balok berada pada titik kesetimbangan (gambar 6b) gaya pegas bernilai nol (x = 0), dan ketika balok bergerak ke kiri (x < 0) menekan pegas (gambar 6c) sehingga pegas menjadi lebih pendek maka gaya pegas memiliki arah ke kanan. Sehingga dari hasil mengamati gambar tersebut kita mengetahui bahwa gaya pegas berfungsi untuk mengembalikan pegas ke posisi awalnya atau posisi kesetimbangan. Hubungan antara gaya pegas dan perubahan panjang dapat pula dilihat dari grafik di bawah ini.
Gambar 7. (a) grafik hubungan antara gaya pegas dengan perubahan panjang pegas, (b) grafik hubungan antara gaya F dengan perubahan panjang pegas, (s) grafik hubungan antara gaya F dengan perubahan panjang pegas untuk beberapa pegas
Perhatikan gambar di atas, gambar 7a menunjukkan hubungan antara gaya pegas dengan perubahan panjang pegas, ketika perubahan panjang pegas bernilai negatif (x < 0 ) maka gaya pegas bernilai positif (Fp > 0) sedangkan ketika perubahan panjang pegas bernilai positif (x > 0) maka gaya pegas bernilai negatif (Fp < 0), nilai perubahan panjang pegas berlawanan dengan nilai gaya pegas hal ini sesuai dengan persamaan di atas dengan tanda minus (-). Gambar 7b sedikit berbeda dengan gambar 7a yakni terletak gaya yang digambarkan, pada grafik 7a gaya yang digambarkan dalam grafik merupakan gaya pegas (gaya pemulih) sedangkan pada grafik 7b gaya yang digambarkan dalam grafik merupakan gaya yang dikerjakan pada pegas yang sesuai dengan persamaan F = kx (tanpa tanda minus) sehingga terlihat bahwa gaya sebanding dengan perubahan panjang pegas, semakin besar gaya yang bekerja maka semakin besar pula perubahan panjang pegasnya. Jika kita analisis lebih lanjut grafik pada gambar 7b merupakan grafik berbentuk garis lurus (linier) yang mana secara matematis memiliki persamaan umum y = mx dimana m merupakan gradien dari grafik tersebut, apabila kita hubungkan antara persamaan garis lurus ini dengan persamaan hukum hooke maka
y = mx → F = kx
kedua persamaan di atas menunjukkan adanya kesesuaian dimana gaya F dianalogikan sebagai sumbu y, perubahan panjang pegas x dianalogikan sebagai sumbu x dan konstanta pegas k dianalogikan sebagai gradien grafik m. Grafik 7c menunjukkan grafik hubungan antara gaya yang bekerja dengan perubahan panjang untuk empat buah pegas, terlihat bahwa perbedaan dari semua grafik tersebut terletak pada kemiringannya (atau gradien), sehingga dengan menggunakan analisis gradien seperti di atas kita dapat mengatakan bahwa semakin curam grafiknya (gradiennya semakin besar) maka nilai konstanta pegasnya juga semakin besar yang artinya pegas tersebut semakin tidak elastis, begitu pula sebaliknya semakin landai grafiknya (gradien semakin kecil) maka nilai konstanta pegasnya semakin kecil yang artinya pegas tersebut semakin bersifat elastis. Jadi jika diurutkan berdasarkan nilai konstanta pegasnya dari terbesar ke terkecil maka k1 > k2 > k3 > k4.
Hubungan antara hukum Hooke dengan Modulus Young
Pada dasarnya baik hukum Hooke dan modulus Young sama-sama berkaitan dengan sifat elastisitas benda, tetapan pegas k berlaku untuk benda – benda elastis yang masih di daerah elastisnya (perhatikan kembali grafik hubungan antara tegangan dan regangan). persamaan hukum Hooke dan persamaan modulus Young memiliki hubungan yang saling berkaitan, jika kita telaah kembali persamaan pada modulus Young dapat kita tulis
Berdasarkan kedua persamaan di atas, maka kita dapat menuliskan persamaan untuk konstanta pegas adalah sebagai berikut
Keterangan :
k = konstanta pegas (N/m)
L = panjang benda (m)
E = Modulus Young (N/m2)
A = luas penampang (m2)
(luas penampang umumnya A = πr2 , dimana r adalah jari-jari)
Hukum Hooke pada susunan pegas
Susunan pegas seri
- Gaya total yang bekerja pada sistem sama dengan Gaya yang bekerja pada masing – masing pegas Ftot = F1 = F2 = ... = Fn
- Pertambahan panjang total sistem pegas adalah hasil penjumlahan pertambahan panjang masing – masing pegas xtot = x1 + x2 + ... + xn
- Konstanta pengganti susunan seri pegas (ks) dapat ditentukan dengan cara
Susunan pegas paralel
- gaya total yang bekerja pada sistem merupakan hasil penjumlahan dari gaya yang bekerja pada masing – masing pegas Ftot = F1 + F2 + ... + Fn
- pertambahan panjang pegas total sistem sama dengan pertambahan panjang masing – masing pegas xtot = x1 = x2 = ... = xn
- Konstanta pengganti susunan paralel pegas (kp) dapat ditentukan dengan cara
Penting












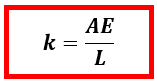

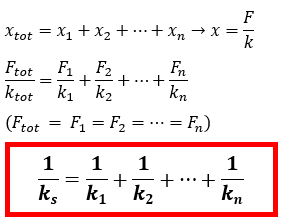
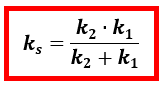
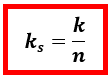

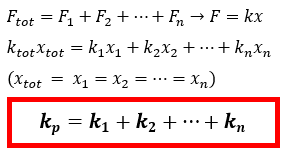


Tidak ada komentar:
Posting Komentar