Alat musik merupakan salah satu instrumen penghasil bunyi yang banyak digunakan dan disukai oleh orang – orang karena dapat menghasilkan nada – nada yang enak di dengar. Gambar di atas menunjukkan dua orang yang bermain alat musik gambar (a) seseorang bermain gitar sedangkan gambar (b) seseorang bermain terompet. Kedua jenis alat musik ini berbeda cara memainkannya jika gitar dengan cara di petik, terompet dengan cara ditiup, bagaimana bisa senar gitar (dawai) kolom udara pada terompet dapat menghasilkan bunyi? oleh karena itu pada kesempatan kali ini kita akan membahas materi tentang gelombang bunyi pada dawai dan pipa organa. Selamat menikmati
Gelombang bunyi pada dawai atau senar
Pada materi gelombang telah dijelaskan terkait dengan superposisi antara gelombang transversal datang dan gelombang transversal pantul akan menghasilkan suatu gelombang stasioner dimana besar amplitudonya berubah – ubah. Titik dimana amplitudo gelombang stasioner bernilai minimum disebut dengan simpul (node) sedangkan titik dimana amplitudo gelombang stasioner bernilai maksimum disebut dengan perut (antinode).
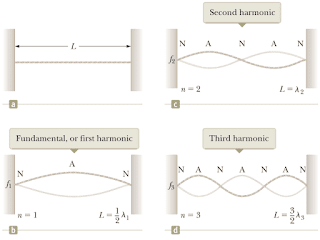
Pada senar gitar atau piano (untuk senar dengan kondisi seperti ini dapat juga kita gunakan istilah “dawai”) kedua ujungnya terikat sehingga pada bagian ini akan terbentuk perut karena senar tidak dapat berosilasi. Ketika suatu dawai bergetar dengan frekuensi tertentu maka pada dawai tersebut akan terbentuk pola simpul dan perut sebagai akibat dari superposisi gelombang yang merambat pada dawai, pada kondisi ini dikatakan bahwa dawai mengalami resonansi dan frekuensinya disebut dengan "frekuensi resonansi". Beberapa bentuk gelombang stasioner pada dawai ketika terjadi resonansi digambarkan seperti berikut ini
Pada gambar 8 di atas kita dapat menganalisis pola – pola yang terbentuk ketika dawai terjadi resonansi dan menentukan frekuensi resonansinya. Gambar 8a menunjukkan dawai sepanjang v yang terikat di kedua ujungnya, kondisi seperti ini dapat kita temui pada senar – senar alat musik seperti : gitar, biola, cello, maupun piano. Ketika kedua ujung dari dawai ini terikat maka senar pada bagian itu tidak dapat bergetar sehingga akan terbentuk simpul di kedua ujungnya.
Gambar 8b adalah ketika terjadi resonansi pertama pada dawai yang bergetar, pada kondisi ini terbentuk dua simpul (disimbolkan dengan “N = node” di kedua ujungnya) dan satu perut (disimbolkan dengan “A = antinode”) di tengah – tengah. Jika kita perhatikan lebih seksama pada pola ini terdapat satu “loop” sebagai akibat dari superposisi gelombang pada dawai dan tali yang sepanjang L akan membentuk gelombang sebesar setengah panjang gelombangnya dan secara matematis dapat ditulis L = ½ λ atau λ = 2L.
Gambar 8c menunjukkan pola pada dawai ketika terjadi resonansi selanjutnya, dimana pada pola ini terbentuk tiga simpul dan dua perut serta ada dua loop maka dari pola resonansi ini kita dapat mengetahui panjang dawai sepanjang L membentuk gelombang sebesar satu panjang gelombang, secara matematis dapat ditulis L = λ. Gambar 8c merupakan pola resonansi selanjutnya yang terbentuk pada dawai, pada pola ini terdapat empat simpul dan tiga perut serta terdapat tiga loop maka dari pola ini dapat diketahui terbentuk gelombang sebesar satu setengah panjang gelombang dan dapat ditulis L = 3/2 λ atau λ = 2/3 L. Jika kita perhatikan dengan seksama ternyata jarak antara suatu resonansi dengan resonansi selanjutnya adalah setengah panjang gelombang.
Berdasarkan ketiga pola awal di atas, kita dapat menuliskan hubungan antara panjang dawai dengan panjang gelombang yang terbentuk pada saat terjadi resonansi adalah
Dimana v merupakan cepat rambat gelombang pada dawai.
Berdasarkan persamaan 19 kita dapat mengetahui bahwa resonansi pada dawai dapat terjadi beberapa tingkat. Pada beberapa sumber terdapat dua istilah untuk pola resonansi ini yakni menggunakan istilah nada dan harmonik kedua istilah ini hanya berbeda namanya saja tapi pada prinsipnya sama. frekuensi resonansi yang terjadi ketika
n = 1 disebut nada dasar atau harmonik ke satu (f1)
n = 2 disebut nada atas pertama atau harmonik ke dua (f2)
n = 3 disebut nada atas kedua atau harmonik ke tiga (f3)
Dst.
Nilai n juga menunjukkan perbandingan frekuensi resonansinya dimana
f1 : f2 : f3 = 1 : 2 : 3
jadi dari nilai perbandingan di atas kita dapat mengetahui bahwa frekuensi harmonik ke tiga (nada atas ke dua) bernilai 3 kali lebih besar daripada frekuensi harmonik ke satu (nada dasar). Selain itu pada dawai kita juga dapat menentukan cepat rambat gelombangnya dengan menggunakan persamaan v = √F/μ. Sehingga kita dapat menuliskan persamaan 19 di atas menjadi.
Keterangan :
F = gaya tegang dawai (N)
ρ = massa jenis dawai (kg/m3)
A = luas penampang dawai (m2)
Gelombang Bunyi pada pipa organa
Pipa organa merupakan suatu alat yang kolom udara dimana salah satu ujungnya di tiup sehingga menimbulkan gelombang stasioner di dalam kolom udara tersebut. perhatikan gambar berikut.
Gambar 9 menunjukkan skema suatu pipa organa, bagian penting dari pipa ini adalah di ujung bawah terdapat bagian yang disebut dengan “Mouth”, dimana pada bagian ini dibuat ada sebuah celah kecil sehingga ketika ada udara yang bergerak melewati celah tersebut akan menimbulkan getaran di dalam kolom udara. Sama halnya dengan dawai, resonansi pada pipa organa akan terjadi dengan pola simpul (node “N”) dan perut (antinode ”A”), perlu diperhatikan bahwa bagian mount akan selalu terbentuk pola perut. Pola simpul dan perut yang terjadi selanjutnya bergantung pada jenis ujung pipa dan panjang kolom udara, sehingga pipa organa dapat dibedakan menjadi 2 jenis yakni pipa organa terbuka dan pipa organa tertutup.
Pipa organa terbuka
Pipa organa terbuka merupakan jenis pipa yang kedua ujungnya dibuat terbuka seperti terlihat pada gambar di bawah ini
Berdasarkan gambar 10 di atas, maka kita dapat mengetahui pada bagian yang ujungnya terbuka akan selalu terbentuk pola perut (antinode “A”), sehingga dapat dikatakan bahwa resonansi pada pipa organa terbuka akan terjadi jika terbentuk perut di kedua ujungnya.
Gambar 10a menunjukkan pola yang terbentuk pada saat terjadi resonansi yang pertama atau disebut juga nada dasar atau harmonik ke satu, ketika terjadi resonansi yang pertama di dalam kolom udara sepanjang L akan terbentuk pola gelombang stasioner sebesar setengah panjang gelombang (L = ½ λ atau λ = 2L). Resonansi selanjutnya yakni nada atas ke satu atau harmonik ke dua akan terjadi ketika di dalam kolom udara terbentuk pola gelombang stasioner sebesar panjang gelombangnya (L = λ) seperti yang terlihat pada gambar 10b. gambar 10c merupakan pola yang terbentuk ketika terjadi resonansi selanjutnya yakni nada atas ke dua atau harmonik ke tiga dimana di dalam kolom udara terbentuk gelombang stasioner sebesar satu setengah panjang gelombang (L = 3/2 λ atau λ = 2/3L)
Berdasarkan ketiga pola awal di atas, kita dapat menuliskan hubungan antara panjang kolom udara dengan panjang gelombang yang terbentuk pada saat terjadi resonansi adalah
Dimana v merupakan cepat rambat gelombang pada udara.
Berdasarkan persamaan 22 kita dapat mengetahui bahwa resonansi pada pipa organa terbuka dapat terjadi beberapa tingkat. Pada beberapa sumber terdapat dua istilah untuk pola resonansi ini yakni menggunakan istilah nada dan harmonik kedua istilah ini hanya berbeda namanya saja tapi pada prinsipnya sama. frekuensi resonansi yang terjadi ketika
n = 1 disebut nada dasar atau harmonik ke satu (f1)
n = 2 disebut nada atas pertama atau harmonik ke dua (f2)
n = 3 disebut nada atas kedua atau harmonik ke tiga (f3)
Dst.
Nilai n juga menunjukkan perbandingan frekuensi resonansinya dimana
f1 : f2 : f3 = 1 : 2 : 3
jadi dari nilai perbandingan di atas kita dapat mengetahui bahwa frekuensi harmonik ke tiga (nada atas ke dua) bernilai 3 kali lebih besar daripada frekuensi harmonik ke satu (nada dasar). Seruling, teromper, dan recorder merupakan contoh alat musik dengan prinsip pipa organa terbuka.
Pipa organa tertutup
Pipa organa tertutup merupakan jenis pipa organa yang salah satu ujungnya tertutup seperti yang terlihat pada gambar di bawah ini.
Berdasarkan gambar 11 di atas, maka kita dapat mengetahui pada bagian yang ujungnya tertutup akan selalu terbentuk pola simpul (node “N”), sehingga dapat dikatakan bahwa resonansi pada pipa organa tertutup akan terjadi jika terbentuk perut di ujung terbuka dan terbentuk simpul di ujung tertutup.
Gambar 11a menunjukkan pola yang terbentuk pada saat terjadi resonansi yang pertama atau disebut juga nada dasar atau harmonik ke satu, ketika terjadi resonansi yang pertama di dalam kolom udara sepanjang L akan terbentuk pola gelombang stasioner sebesar seperempat panjang gelombang (L = ¼ λ atau λ = 4L). Resonansi selanjutnya yakni nada atas ke satu atau harmonik ke dua akan terjadi ketika di dalam kolom udara terbentuk pola gelombang stasioner sebesar tiga perempat panjang gelombangnya (L = 3/4λ atau λ = 4/3L) seperti yang terlihat pada gambar 11b. gambar 11c merupakan pola yang terbentuk ketika terjadi resonansi selanjutnya yakni nada atas ke dua atau harmonik ke tiga dimana di dalam kolom udara terbentuk gelombang stasioner sebesar lima perempat panjang gelombang (L = 5/4λ atau λ = 4/5L)
Berdasarkan ketiga pola awal di atas, kita dapat menuliskan hubungan antara panjang kolom udara dengan panjang gelombang yang terbentuk pada saat terjadi resonansi adalah
Dimana v merupakan cepat rambat gelombang pada udara.
n = 3 disebut nada atas pertama atau harmonik ketiga (f3)
n = 5 disebut nada atas kedua atau harmonik ke lima (f5)
Dst.
Nilai n juga menunjukkan perbandingan frekuensi resonansinya dimana
f1 : f2 : f3 = 1 : 3 : 5
jadi dari nilai perbandingan di atas kita dapat mengetahui bahwa frekuensi harmonik ke tiga (nada atas ke dua) bernilai 3 kali lebih besar daripada frekuensi harmonik ke satu (nada dasar). Perlu diperhatikan disini untuk pipa organa tertutup berbeda dengan pipa organa terbuka dimana nilai “n” merupakan kelipatan bilangan ganjil saja.
Contoh soal
Soal nomor 1
Soal nomor 2
Soal nomor 3
Soal nomor 4
Soal nomor 5
Soal nomor 6
Perhatian : frekuensi resonansi kelima tak sama dengan frekuensi harmonik kelima
Soal nomor 7
Soal nomor 8
Soal nomor 9
Soal nomor 10
Terjemahan :
Sebuah pipa organa memiliki dua frekuensi resonansi berurutan sebesar 1372 Hz dan 1764 Hz. (a) apakah jenis pipa organa yang digunakan? (b) pada nada berapakah frekuensi resonansi tersebut? (c) berapakah panjang kolom udara pipa organa?









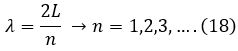
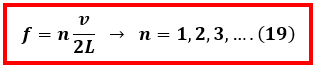
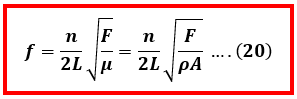


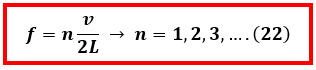
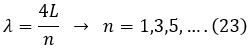
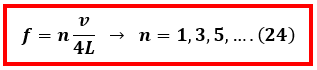

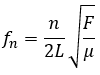
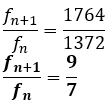

Tidak ada komentar:
Posting Komentar