Banyak orang suka mendengarkan musik melalui gagdet atau smartphone mereka menggunakan headset maupun secara langsung, ketika mendengarkan musik tentunya mereka akan menyesuaikan volumenya tidak terlalu pelan atau terlalu kencang karena ketika musik di dengarkan terlalu kencang akan menyakit telinga si pendengar. Pada saat mengubah volumenya tersebut pada dasarnya mengubah salah satu karakteristik dari gelombang bunyi yakni intensitas gelombang bunyi yang di keluarkan gadget atau smartphone mereka selain itu taraf intensitas bunyi atau “tingkat kebisingan” juga akan mempengaruhi kenyamanan ketika mendengarkan musik. Oleh sebab itu pada kesempatan kali ini kita akan membahas tentang intensitas bunyi dan taraf intensitas bunyi.
Intensitas Bunyi
Sama seperti gelombang pada umumnya, gelombang bunyi yang merambat melalui suatu medium juga akan menghantarkan energi dari satu daerah ke daerah yang lainnya. rata – rata energi tiap waktu yang dipancarkan gelombang bunyi persatuan luas yang tegak lurus terhadap arah rambatnya disebut dengan ”intensitas bunyi”. Energi tiap waktu yang dipindahkan oleh gelombang bunyi ini disebut dengan daya, yang mana dalam fisika daya juga dapat dirumuskan sebagai berikut.P = F . v
Dimana F merupakan gaya yang dapat kita hubungkan dengan besaran tekanan amplitudo (F = Pmax (x,t) . A) sedangkan v merupakan kecepatan yang dapat kita hubungan dengan besaran perpindahan amplitudo gelombang (v = d y(x,t)/dt). sehingga persamaan daya di atas dapat ditulis
P = [Pmax (x,t) A] . [dy(x,t)/dt ]
Perlu di perhatikan notasi “P” menunjukkan tekanan dan notasi “Pmax” menunjukkan tekanan amplitudo. Dengan mensubstitusikan persamaan (1) dan (3) pada materi cepat rambat bunyi maka persamaan di atas dapat ditulis
P = [BkymaxA sin (kx – ωt)] . [d/dt ] ymax cos (kx – ωt)
Pada persamaan di atas perpindahan amplitudo ditulis sebagai “ymax” untuk menghindari notasi yang saman dengan luas penampang “A” . “B” adalah modulus bulk medium dimana B = v2ρ konstanta gelombang “k” dapat ditulis sebagai k = ω/v sehingga persamaan di atas menjadi
P = ρvωymaxA sin (kx – ωt)[ωymax sin (kx – ωt)
P = ρvω2ymax2A sin2 (kx – ωt)
Untuk sembarang x nilai rata – rata untuk persamaan sin2 (kx – ωt) dalam satu periode T adalah ½ maka persamaan di atas menjadi
P = ½ρvω2ymax2A
Seperti yang telah dijelaskan sebelumnya bahwa intensitas gelombang bunyi merupakan energi tiap waktu (daya) yang dipancarkan gelombang bunyi persatuan luas yang tegak lurus terhadap arah rambatnya, hal ini dapat dituliskan secara matematis sebagai berikut
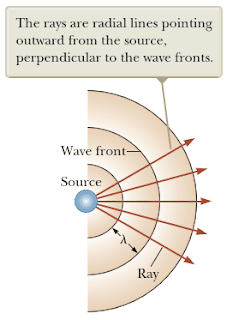
Jika pada bagian sebelumnya kita menggambarkan perambatan gelombang bunyi dalam satu dimensi (sumbu x) hal ini dilakukan untuk mempermudah pemahaman, akan tetapi pada kenyataannya gelombang bunyi yang merambat bergerak dalam koordinat tiga dimensi. Perambatan gelombang bunyi dapat diilustrasikan sebagai berikut.
Jika suatu gelombang bunyi merambat dalam medium yang sama maka gelombang tersebut akan merambat ke segala arah dengan kecepatan yang sama sehingga menghasilkan suatu bentuk gelombang bunyi dalam koordinat tiga dimensi menyerupai bentuk bola seperti yang diilustrasikan pada gambar 6 di atas. setiap busur merepresentasikan suatu permukaan dengan fase gelombang yang konstan yang disebut dengan muka gelombang. Jarak antar muka gelombang yang memiliki fase gelombang sama adalah panjang gelombang (λ). Garis radial yang mengarah keluar dari sumber merepresentasikan arah rambat gelombang yang disebut dengan “ray”.
Berdasarkan ilustrasi tersebut kita dapat mengetahui bahwa “bentuk” dari gelombang bunyi adalah bola, sehingga luas permukaan yang dimaksudkan di persamaan 11 adalah luas permukaan bola (A = 4πr2). Maka persamaan 11 dapat ditulis ulang menjadi
Pengaruh jarak dari sumber bunyi pada Intensitas Bunyi
Perhatikan kembali gambar 6 di atas, berdasarkan gambar tersebut terlihat bahwa semakin jauh dari sumber bunyi maka luasan yang mendapat pengaruh dari gelombang bunyi semakin besar akibatnya energi akan terdistribusi ke wilayah atau daerah yang lebih besar akibatnya intensitas bunyi yang terdengar akan semakin kecil. Hal ini juga dapat dilihat dari persamaan 12 dimana Intensitas bunyi berbanding terbalik dengan kuadrat jarak dari sumber bunyi yang artinya semakin jauh dari sumber bunyi (semakin besar) maka intensitas bunyinya yang akan semakin kecil. Sehingga kita dapat menuliskan persamaan perbandingan antara Intensitas bunyi dengan jarak adalah
Taraf intensitas (TI) pada gelombang bunyi
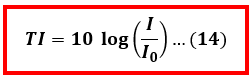
Sering kita alami dalam di sekitar, ketika kita mendengar bunyi ada yang terdengar keras ada yang terdengar pelan, kadang kita mengatakan bunyi yang terdengar sangat keras seperti suara mesin jet, mesin pabrik, atau konser band rock dengan kata “bising”. Secara sederhana Taraf Intensitas Bunyi dapat dikatakana tingkat kebisingan yang ditimbulkan dari suatu sumber bunyi, semakin besar Taraf Intensitas (TI) bunyi maka bunyi akan terdengar semakin bising. Besarnya tarah intensitas ini dipengaruhi oleh intensitas sumber bunyi dengan fungsi logaritmik berikut.
TI : Taraf Intensitas (dB)
I : Intensitas sumber bunyi (W/m2)
I0 : Intensitas Ambang Pendengaran (10-12 W/m2)
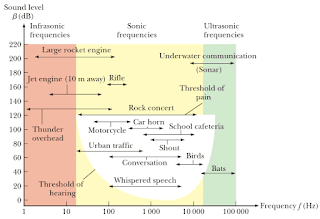
Intensitas Ambang Pendengaran sebesar 10-12 W/m2 dipilih sebagai referensi karena Intensitas ini sebagai perkiraan frekuensi ambang pendengaran sebesar 1 KHz. Berdasarkan taraf intensitas batas ambang nyeri pendengar adalah ketika intensitas bunyinya sebesar 1,00 W/m2 sehingga memiliki taraf intensitas TI = 10 log (1 / 10-12) = 10 log 1012 = 120 dB, sedangkan batas ambang pendengar adalah ketika intensitas bunyinya sebesar 10-12 W/m2 sehingga memiliki taraf intentsitas TI = 10 log (10-12 / 10-12) = 10 log 0 = 0 dB. berdasarkan penjelasan tersebut kita dapat mengetahui juga kita mendengar suatu bunyi yang taraf intensitasnya lebih besar 120 dB maka telinga kita akan terasa sakit (batas ambang nyeri pendengaran) sedangkan jika ada bunyi dengan taraf intensitas lebih kecil dari 0 dB maka kita tidak dapat mendengar bunyi tersebut. untuk lebih memahaminya perhatikan gambar berikut
Perhatikan gambar 7 di atas daerah yang berwarna putih merupakan daerah yang mampu di dengar oleh manusia, untuk daerah di atasnya jika kita mendengar bunyi dengan taraf intensitas tersebut maka telinga kita akan sakit. Begitu pula sebaliknya jika ada bunyi dengan taraf intensitas di bawah daerah berwarna putih maka kita tidak akan bisa mendengarnya.
Kembali lagi ke persamaan 14 di atas, persamaan tersebut merupakan persamaan logaritmik. Perhatikan bahwa nilai logaritma 10 sama dengan 1, sehingga tiap kenaikan taraf intensitas 10 dB intensitas bunyinya meningkat dengan faktor 10 pangkat. Misalkan ketika taraf intensitas bunyinya meningkat 40 dB maka intensitas bunyinya meningkat sebesar 104 kali dari keadaan awal. Beberapa intensitas dan taraf intensitas sumber bunyi yang sering kita dengar dapat dilihat pada tabel di bawah ini
Tabel 2. Taraf intensitas bunyi dari beberapa sumber bunyi
|
Sumber bunyi |
Taraf Intensitas Bunyi, TI
(dB) |
Intensitas Bunyi, I (W/m2) |
|
Pesawat jet militer Konser musik rock Alat rivet Kereta layang Jalanan macet Percakapan Mobil berjalan Menyalakan radio di rumah Berbisik Gemersik daun Batas ambang pendengaran pada 1000 Hz |
140 130 120 95 90 70 65 50 40 20 10 0 |
102 101 1 3,2 x 10-3 10-3 10-5 3,2 x 10-6 10-7 10-8 10-10 10-11 10-12 |
Besarnya taraf intensitas juga bisa berubah karena dua hal yakni perubahan jumlah sumber bunyi dan perubahan jarak dari sumber bunyi.
Perubahan taraf intensitas karena perubahan jumlah
Untuk sumber bunyi yang identik, ketika jumlah sumber bunyi berubah maka tingkat kebisingan yang ditimbulkan juga berubah sehingga taraf intensitasnya juga berubah. Semakin banyak jumlah sumber bunyinya maka taraf intensitasnya juga akan semakin besar. Secara matematis dapat ditulis
TI2 = taraf intensitas akhir
TI1 = taraf intensitas awal
n = jumlah mesin
Perubahan taraf intensitas karena perubahan jarak
Perubahan jarak dari sumber juga akan mempengaruhi intensitas bunyi yang di dengar, semakin dekat dari sumber bunyi maka taraf intensitasnya akan semakin kecil. Begitu pula sebaliknya semakin jauh dari sumber bunyi maka taraf intensitasnya akan semakin besar. persamaan matematisnya adalah sebagai berikut.
r2 : jarak akhir dari sumber bunyi
jika dalam sebuah peristiwa terjadi perubahan jumlah sumber bunyi dan jarak dari sumber bunyi maka untuk dapat menentukan taraf intensitasnya kita dapat menggabungkan persamaan 15 dan 16 seperti berikut ini
Contoh Soal
Soal nomor 1
Soal nomor 2
Soal nomor 3
Soal nomor 4
Soal nomor 5
Soal nomor 6
Soal nomor 7
Soal nomor 8
Soal nomor 9
Soal nomor 10
Soal nomor 11
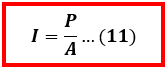
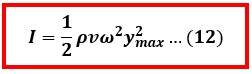
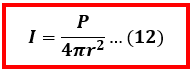
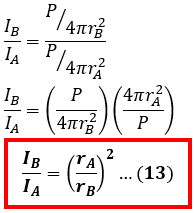
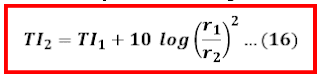
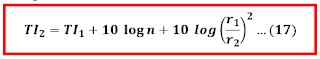
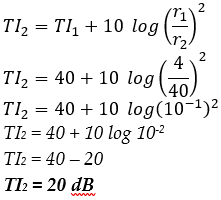
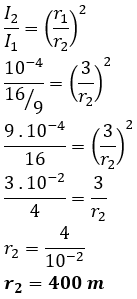
Tidak ada komentar:
Posting Komentar