Kupas tuntas! materi dinamika rotasi (fisika kelas 11)

Gambar 1. Atlet judo ketika membanting lawannya

Seorang atlet judo ketika akan membanting lawannya, ia akan berusaha menempatkan titik pusat massa lawannya sedekat mungkin dengan pusat massa dirinya untuk mengurangi torsi yang disebabkan oleh lawannya tersebut, sehingga hanya torsi dirinya sendiri yang bekerja pada saat membanting. Berbicara tentang gerak rotasi (gerak melingkar) pada dasarnya mirip dengan gerak translasi (gerak lurus) baik secara teknik analisis atau persamaan-persamaan matematisnya. Pada dasarnya gerak rotasi merupakan gerak lurus yang ditarik ke suatu titik secara terus menerus sehingga lintasannya menjadi melingkar. Gaya yang menarik tersebut disebut dengan gaya sentripetal.

Sebelum mempelajari lebih lanjut tentang dinamika rotasi, penting untuk mengetahui hubungan antara besaran-besaran dalam gerak translasi dengan besaran-besaran dalam gerak rotasi. Hal ini dikarenakan keduanya saling berkaitan seperti yang terlihat pada tabel di bawah ini

Dinamika Rotasi

Dinamika rotasi berarti bahwa gerak benda adalah gerak rotasi (melingkar) dengan mempertimbangkan gaya-gaya yang bekerja pada benda tersebut saat bergerak. Pada materi ini saya bagi menjadi beberapa bagian yang perlu dipahami antara lain: torsi, momen inersia, momentum sudut, dan hukum kekekalan pada benda yang berotasi serta analisis dinamika rotasi. Selain itu perlu dipahami bahwa ketika benda berotasi pasti ada titik pusat (titik poros) dari gerakan tersebut.

Torsi

Torsi sering disebut juga sebagai momen gaya, Berdasarkan tabel di atas terlihat bahwa torsi identik dengan gaya, jika gaya biasanya bekerja ketika benda bergerak lurus (translasi) akan tetapi torsi ini dapat dikatakan sebagai gaya ketika benda bergerak melingkar. Torsi merupakan besaran vektor yang memiliki nilai (besar) dan arah.

Menentukan besar torsi

Faktor-faktor apa saja yang mempengaruhi besarnya torsi, untuk itu Perhatikan gambar berikut.

Gambar 2. Gaya yang bekerja dengan jarak yang berbeda

(sumber: essential university physics)

Berdasarkan gambar 2, terlihat bahwa semakin jauh dari titik pusat (O) maka besarnya torsi juga akan semakin besar, hal ini menunjukkan bahwa torsi sebanding dengan jarak gaya terhadap titik pusat (O)

Gambar 3. Gaya yang bekerja dengan sudut yang berbeda-beda

(sumber: essential university physics)

Berdasarkan gambar 3, semakin tegak lurus gaya dengan titik pusat (O) maka semakin besar torsinya hingga akan mencapai nol ketika gaya sejajar dengan titik pusat (O). Perlu diketahui jika torsi sama dengan nol, artinya tidak ada gerakan memutar dari benda tersebut. ketika sebuah gaya bekerja dengan sudut tertentu (gambar 2b) maka kita perlu memproyeksikan gaya tersebut terhadap sumbu x dan sumbu y seperti yang terlihat pada gambar berikut.

Gambar 4. Proyeksi gaya dan jarak

(sumber: essential university physics)

Gambar 4 memberikan informasi bahwa ketika sebuah gaya bekerja dengan membentuk sudut terhadap titik pusatnya maka harus dicari komponen antara gaya dan jarak yang saling tegak lurus karena komponen tersebut yang memberikan torsi sedangkan komponen yang saling sejajar tidak memberikan torsi (tidak menyebabkan putaran). Untuk menentukan komponen yang saling tegak lurus dapat dilakukan dengan memproyeksikan gaya (gambar 4a) atau memproyeksikan jaraknya (gambar 4b) hal ini bergantung dari soal yang diberikan lebih mudah yang mana.

Berdasarkan penjelasan di atas, maka dapat kita ketahui bahwa torsi dipengaruhi oleh besarnya gaya, jarak terhadap titik pusat atau porosnya, serta besarnya sudut antara gaya dan poros (jika belum tegak lurus, ditegak luruskan), sehingga secara matematis persamaan torsi dapat ditulis sebagai berikut

Keterangan :

τ : torsi (Nm)

F : gaya (N)

r : jarak terhadap poros (m)

θ : sudut antara gaya dan jarak

Menentukan arah torsi

Dalam menentukan arah torsi dapat digunakan aturan kaidah tangan kanan sebagai berikut

Gambar 5. Kaidah tangan kanan untuk menentukan arah torsi

(sumber : Physics University)

Kaidah tangan kanan untuk menentukan arah vektor terlihat seperti pada gambar 5 di atas, dimana empat jari sebagai arah putaran gaya dan ibu jari sebagai arah torsi. jika gaya diputar berlawanan arah dengan arah jarum jam, maka arah torsinya ke atas (gambar 5a), akan tetapi jika gaya diputar searah dengan arah jarum jam, maka arah torsinya ke bawah (gambar 5b).

Ingatlah!

Konsep ini akan sangat berguna ketika kamu akan memasang atau melepaskan baut atau mur, tinggal genggam kunci pas atau obeng kemudian arahkan jempol masuk jika ingin memasang dan arahkan jempol keluar jika ingin melepas kemudian putar sesuai dengan arah empat jarinya.

Penerapan konsep ini agak berbeda jika diterapkan dalam mengerjakan soal, jika mengerjakan soal arah torsi diwakili dengan arah putaran gaya yang bekerja. jika gaya diputar berlawanan arah dengan arah jarum jam maka torsi bernilai positif dan jika gaya diputar searah dengan arah jarum jam maka torsi bernilai negatif.

Resultan torsi

Jika beberapa gaya bekerja pada sebuah poros maka akan berdampak munculnya beberapa torsi dari gaya-gaya tersebut, resultan torsinya perlu diperhatikan juga arahnya karena torsi juga merupakan besaran vektor. perhatikan contoh soal berikut ini.

contoh soal

Pada batang yang massanya 2 kg dan panjang 100 cm bekerja tiga gaya masing-masing F₁ = 2N, F₂ = 5N, dan F₃ = 4N

Jarak BD = 60 cm, BC = 20 cm, dan titik pusat massa di titik Z. Momen gaya terhadap titik B adalah ... (g = 10 m/s²)

a. 0,4 Nm

b. 0,8 Nm

c. 4,2 Nm

d. 4,6 Nm

E. 6,2 Nm

pembahasan soal:

Momen Inersia

Momen inersia merupakan kemampuan benda untuk mempertahankan posisinya terhadap perubahan rotasinya. Momen inersia ini identik dengan massa jika gerakannya adalah gerak translasi (gerak lurus) seperti yang terlihat pada tabel 1 di atas. Dengan kata lain, jika benda tidak mengalami bergerak rotasi terhadap titik pusat (sumbu porosnya) maka benda tersebut tidak memiliki momen inersia. Momen inersia benda partikel

Momen inersia partikel yakni benda dianggap sebagai suatu satu titik partikel bermassa, jika benda tersebut melakukan gerak rotasi maka benda akan memiliki momen inersia yang secara matematis dapat ditulis

Keterangan :

I : momen inersia (kgm²)

m : massa (kg)

r : jarak terhadap poros (m)

Berbeda dengan torsi yang merupakan besaran vektor, momen inersia adalah besaran skalar, sehingga jika sebuah benda tegar yang terdiri dari banyak partikel yang terpisah dan masing-masing memiliki massa berbeda-beda momen inersia total benda tersebut dapat ditentukan dengan cara menjumlahkan momen inersia masing-masing partikel tanpa mempertimbangkan arahnya, secara matematis momen inersia total dapat ditulis sebagai berikut.

Contoh soal

Sebuah benda tegar terdiri dari 4 buah partikel bermassa seperti yang ditunjukkan oleh gambar berikut

Jika benda diputar dengan poros di sumbu y. Tentukan besar momen inersia benda tersebut!

pembahasan soal:

Momen inersia benda tegar dengan massa terdistribusi kontinu

jika sebuah benda bukan merupakan partikel, akan tetapi benda memiliki massa dan bentuk tertentu maka untuk menentukan momen inersia benda tersebut kita bayangkan bahwa tiap benda tersusun atas elemen-elemen massa kecil yang berjarak r dari porosnya, perhatikan gambar berikut.

Gambar 6. Visualisai elemen massa suatu benda yang berotasi terhadap porosnya

(sumber : essential university physics)

Sejumlah elemen massa yang berjarak r dari porosnya kemudian berputar bersama-sama seperti yang terlihat pada gambar 6 di atas, dapat kita tentukan momen inersia total dari benda tersebut dengan melakukan integrasi terhadap elemen massanya yang secara matematis dapat ditulis sebagai berikut!

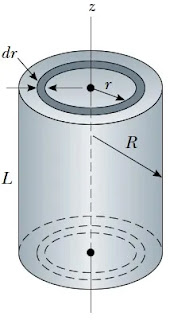
Misalnya untuk menentukan momen inersia sebuah silinder pejal yang berputar pada poros tengahnya seperti gambar berikut.

Gambar 7. Silinder pejal yang berputar pada porosnya (sumbu z)

sumber: physisc for scientists and engineers)

Sebuah silinder pejal yang memiliki jari-jari R (jari-jari ini dibagi menjadi elemen-elemen kecil jari-jari r yang dengan elemen terkecilnya adalah dr)dengan dan tinggi L yang berputar pada porosnya di sumbu z seperti pada gambar 7 di atas, untuk mengetahui momen inersia pada silinder tersebut dapat dilakukan dengan cara (batas integral dari 0 sampai R)

Dengan cara yang sama kita dapat mengetahui momen inersia untuk beberapa benda seperti yang ditunjukkan dalam tabel berikut

Teorema Sumbu sejajar

Teorema sumbu sejajar memungkinkan kita untuk mengetahui momen inersia benda ketika titik poros benda bergeser dari titik pusat massanya ke titik yang lainnya. perhatikan gambar berikut

Gambar 8. Elemen massa m_i yang memiliki koordinat (x_i, y_i) dari pusat massanya dan memiliki koordinat (x_i – a, y_i – b) jika ditinjau dari titik P yang sejajar dengan pusat massanya

(sumber: physics university)

Misalkan sebuah benda memiliki berotasi dengan pusat massa sebagai porosnya, yang kemudian porosnya bergeser ke titik P yang sejajar dengan pusat massa dengan koordinat (a, b) sehingga memiliki jarak d dari pusat massanya (d² = a² + b²)seperti yang terlihat pada gambar 8 di atas. Untuk menentukan momen inersia benda tersebut setelah poros rotasinya berubah ke titik P, kita tinjau elemen massa m_i. Dengan menggunakan persamaan (4), maka kita dapat mengetahui Momen inersia mi ketika poros di pusat massa (I_pm) adalah

Persamaan pertama sama dengan momen inersia ketika poros berada di titik pusat massa (I_pm), persamaan yang kedua sama dengan nol karena kita hanya menggunakan titik pusat massa dan titik P sebagai porosnya, dan persamaan ketiga dapat kita tuliskan Md² jadi persamaan matematis untuk teorema sumbu sejajar ini dapat kita tuliskan sebagai berikut.

Keterangan :

I_P : momen inersia dengan poros di P (kgm²)

I_pm : momen inersia dengan poros di pusat massa (kgm²)

M : massa (kg)

d : jarak pergeseran dari pusat massa (m)

Persamaan (5) dapat kita gunakan untuk membuktikan beberapa momen inersian benda yang terdapat pada tabel di atas.

Contoh soal

sebuah batang pejal homogen bermassa M dan panjang L ditunjukkan seperti gambar berikut.

Ketika diputar dengan poros pusat massanya (titik O), batang memiliki momen inersia sebesar 1/12 ML². Tentukan besar momen inersia batang jika porosnya bergeser ke salah satu ujungnya (sumbu y’)!

pembahasan soal:

Analogi hukum II Newton pada gerak rotasi

Sebuah partikel bermassa bergerak melingkar dengan jari-jari r yang dipengaruhi oleh gaya tangensial Ft dan gaya sentripetal Fs, seperti yang ditunjukkan oleh gambar berikut.

Gambar 9. Partikel bermassa m yang bergerak melingkar dengan dipengaruhi oleh gaya tangensial Ft dan gaya sentiperal Fs

(sumber: physics for scientists and engineers)

Torsi yang timbul dari partikel tersebut dikarenakan adanya gaya tangensial bukan gaya sentripetal hal ini dikarenakan gaya sentripetal arahnya langsung menuju ke poros sehingga tidak menimbulkan torsi (baca kembali bagian torsi di atas.

Besarnya gaya tangensial dapat ditentukan dengan persamaan

F_t = ma_t

Besarnya torsi dengan poros di pusat lingkaran karena gaya tangensial adalah

τ = F_t r

τ = ma_t r (a = αr , lihat kembali tabel pertama)

τ = m α r² (mr² = I)

Keterangan :

τ : torsi (Nm)

I : momen inersia (kgm²)

α : percepatan sudut (rad/s²)

persamaan (6) di atas, pada dasarnya analogi hukum II Newton (F = m.a) untuk gerak melingkar. Hal ini terlihat dari besarannya yakni torsi (τ) indetik dengan gaya (F) pada gerak translasi, momen inersia (I) identik dengan massa (m), dan percepatan sudut (α) identik dengan percepatan translasi (a). Torsi juga merupakan besaran vektor jadi memiliki besar dan arah, sehingga jika ada beberapa buah gaya yang bekerja pada suatu benda maka persamaan di atas dapat ditulis sebagai berikut.

Jika kita kombinasikan dengan persamaan (1) dengan gaya-gaya yang bekerja tegak lurus terhadap poros, maka persamaan (7) dapat kita tulis sebagai berikut

Momentum Sudut

Analog dengan gerak translasi dimana terdapat momentum linier, pada gerak rotasi juga terdapat momentum sudut atau momentum angular. Massa (m) identik dengan momen inersia (I), kecepatan linier (v) identik dengan kecepatan sudut (ω). Sehingga secara matematis momentum sudut dapat ditulis dengan persamaan

Keterangan :

L : momentum sudut (kgm²/s)

I : momen inersia (kgm²)

ω : kecepatan sudut (rad/s)

momentum sudut merupakan besaran vektor sehingga memiliki gaya dan arah, untuk menentukan arah dari momentum sudut digunakan kaidah tangan kanan seperti ketika menentukan arah dari torsi. Perhatikan gambar di bawah ini

Gambar 10. (a) diagram vektor momentum sudut, (b) kaidah tangan kanan untuk menentukan arah momentum sudut

(sumber : fundamentals of physics and physics university

Berdasarkan gambar 10, terlihat adanya hubungan antara kecepatan linier (v) dengan kecepatan sudut (ω) yakni ω = vr dan dengan memasukkan I = mr². Sehingga persamaan (9) dapat ditulis

Hukum kekekalan momentum sudut

Sejalan dengan momentum linier yang mana jika tidak ada gaya luar yang bekerja pada suatu sistem, maka momentum sistem tidak mengalami perubahan (disebut dengan hukum kekekalan momentum linear), demikian pula pada gerak rotasi berlaku hukum kekekalan momentum sudut yang berbunyi “jika tidak ada momen gaya luar yang bekerja pada sistem, maka momentum sudut sistem tidak berubah (kekal)”. Secara matematis dapat ditulis.

Hukum kekekalan momentum ini memberikan dampak yang cukup besar bagi gerak suatu sistem, perhatikan gambar di bawah ini

Gambar 11. (a) penari balet yang merenggangkan tangan dan kakinya, (b) penari balet yang merampingkan tangan dan kakinya

(sumber : essential university physics)

Berdasarkan gambar 11, ketika penari balet sedang merenggangkan tangan dan kakinya yang berarti jauh dari poros (gambar 11a), maka momen inersia penari akan besar dan kecepatan sudutnya kecil sehingga ia berputar dengan lambat. Akan tetapi ketika kedua tangan dan kaki dirapatkan ke tubuhnya (gambar 11b) maka momen inersianya akan semakin kecil, sehingga berdasarkan hukum kekekalan momentum sudut semakin kecilnya momen inersia akan diimbangi dengan semakin besarnya kecepatan sudut sehingga penari akan berputar lebih cepat.

Contoh soal

Seorang profesor fisika berdiri di tengah meja putar yang licin dengan lengan teregang dan membawa barbel bermassa 5 kg pada masing-masing tangannya seperti ditunjukkan pada gambar di bawah ini.

Kemudian ia berputar pada porosnya dengan waktu 2,0s untuk satu kali putaran. tentukan kecepatan sudutnya jika kemudian ia meletakkan barbelnya di perut? (momen inersia profesor tanpa barbel sebesar 3,0 kgm² dengan tangan terentang dan 2,2 kgm² ketika tangannya di perut. Barbel berada 1,0 m pada awalnya dan 0,20 m setelah berputar)

pembahasan soal:

Energi kinetik rotasi

Setiap benda yang bergerak memiliki energi kinetik, ungkapan ini sering kita dengar ketika mempelajari materi tentang energi dan sering kita gunakan untuk benda – benda yang bergerak di lintasan yang lurus seperti gerak mobil di jalan raya, gerak benda yang jatuh, atau gerak benda yang dilempar vertikal ke atas. Bagaimana jika benda tersebut tidak bergerak lurus tapi bergerak melingkar, seperti gambar bianglala di bawah ini. Apakah benda tersebut memiliki energi kinetik?

Gambar 12. Bianglala yang berputar

Benda yang begerak melingkar juga memiliki energi kinetik yang disebut dengan energi kinetik rotasi. Energi kinetik rotasi ini merupakan analogi dari energi kinetik translasi pada gerak lurus, jika kita mengetahui bahwa benda yang bergerak lurus dengan kecepatan v memiliki energi kinetik sebesar EK = ½ mv², massa (m) identik dengan momen inersia (I) dan kecepatan linier (v) identik dengan kecepatan sudut (ω), sehingga energi kinetik rotasi secara matematis dapat ditulis sebagai berikut.

Keterangan :

EKR : energi kinetik rotasi (J)

I : momen inersia (kgm²)

ω : kecepatan sudut benda (rad/s)

Pada kenyataannya banyak benda yang tidak hanya bergerak translasi saja atau bergerak rotasi saja akan tetapi bergerak translasi dan rotasi secara bersamaan, contohnya bola yang menggelinding, roda mobil dll. Perbedaan antara benda yang hanya bergerak translasi saja, bergerak rotasi saja, dan bergerak keduanya secara bersamaan dapat dilihat pada gambar berikut

Gambar 13. (a) gerak translasi, (b) gerak rotasi, (c) kombinasi gerak translasi dan rotasi

Gambar 13a merupakan diagram ketika sebuah benda bergerak translasi dimana titik pusat massanya bergerak lurus dengan kecepatan vpm dan diikuti oleh semua bagian dari benda tersebut memiliki kecepatan linear dan arah yang sama dengan kecepatan pusat massa (pm), gambar 13b merupakan diagram ketika sebuah benda bergerak rotasi, terlihat titik pusat massanya berputar dengan kecepatan sudut ω diikuti semua bagian benda tersebut berputar dengan kecepatan sudut yang sama, bagian terluar dari bola mengalami gerak translasi yang besarnya sama dengan v = rω dengan arah yang berbeda-beda sesuai dengan posisinya. Gambar 13c merupakan benda yang mengalami gerak translasi dan gerak rotasi secara bersamaan, perlu diperhatikan disini bahwa bagian atas dari benda memiliki kecepatan linear dan kecepatan sudut sehingga kecepatan total di titik ini sebesar v = v + rω = 2rω, sedangkan bagian bawah yang bergesekan dengan permukaan lantai tidak memiliki kecepatan v = 0 hal ini dikarenakan secara vektor kecepatan linear dan kecepatan sudut di titik ini saling berlawanan (kebalikan dengan di titik atas).

Berdasarkan penjelasan di atas, maka dapat kita simpulkan bahwa ketika benda bergerak translasi maka ia hanya memiliki energi kinetik translasi, ketika benda bergerak rotasi maka ia hanya memiliki energi kinetik rotasi, dan ketika benda bergerak rotasi dan translasi secara bersamaan maka ia memiliki energi kinetik translasi dan energi kinetik rotasi yang secara matematis dapat ditulis:

Keterangan :

EK_tot = energi kinetik total (J)

EK_T = energi kinetik translasi (J)

EK_R = energi kinetik rotasi (J)

Tips :

Gerakan benda yang bergerak secara translasi dan rotasi sering disebut dengan menggelinding. Dalam menganalisis benda yang bergerak menggelinding perlu diperhatikan bentuk benda tersebut hal ini karena berkaitan dengan konstanta pada momen inersia benda.

Analisis dinamika rotasi

Pada bagian ini kita akan membahas beberapa contoh penerapan dinamika rotasi yang sering dijumpai dalam soal, saya membaginya menjadi beberapa kategori dengan tujuan tiap kategori menggunakan konsep yang sama meskipun model soalnya berbeda-beda. Kategori yang saya maksud antara lain : sistem partikel bermassa, sistem katrol, sistem bidang miring, penggabungan dua roda, mari kita bahas satu-persatu

Sistem partikel bermassa

Sistem partikel bermassa yang dimaksudkan disini adalah ketika sebuah benda tegar yang terdiri dari beberapa partikel bermassa (digambarkan dalam titik) berputar terhadap suatu poros dan diminta untuk menentukan momen inersia dari benda tersebut.

Tips :

Perhatikan letak sumbu porosnya untuk menentukan jarak partikel terhadap poros (nilai r)
Momen inersia adalah besaran skalar, jadi tinggal dijumlahkan saja tanpa memperhatikan arah gerak partikel,
Hanya partikel yang berputar terhadap poros yang memiliki momen inersia, sedangkan partikel yang tidak berputar tidak memiliki momen inersia (I = 0)

Contoh :

1. sebuah benda tegar terdiri atas sistem partikel bermassa yang digambarkan sebagai berikut

Jika benda tersebut berputar terhadap poros di titik O, tentukan besar momen inersia benda tersebut!

pembahasan soal:

2. Sebuah bagian dari mesin terdiri atas tiga piringan (I = mr²) yang dihubungkan dengan kawat yang ringan seperti pada gambar berikut!

a) tentukan momen inersia sistem jika poros berada di piringan A dan menembus piringan (tegak lurus gambar)

b) tentukan momen inersia sistem jika poros berada di pusat piringan B dan C

pembahasan soal:

Sistem katrol

Sistem katrol yang dimaksudkan disini adalah suatu sistem yang terdiri dari sebuah katrol yang dihubungkan dengan minimal satu buah benda (bisa lebih), sedikit berbeda dengan ketika belajar tentang dinamika gerak dimana katrol dianggap licin sehingga tidak bergerak, akan tetapi pada dinamika rotasi katrolnya berputar sehingga perlu diperhitungkan torsi yang terjadi pada katrol.

Tips :

Gambarkan gaya-gaya yang bekerja pada sistem, pisahkan gerakan masing-masing benda (katrol dan benda)
Analisis masing-masing benda menggunakan hukum II Newton (baik untuk translasi maupun untuk rotasi)
Gunakan metode eliminasi dan substitusi untuk menemukan variabel yang dicari.

Contoh :

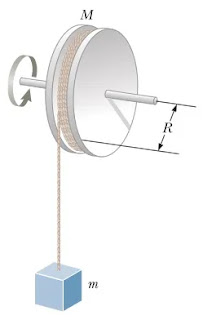
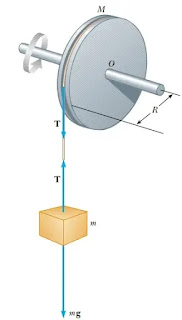
1) sebuah benda bermassa m = 5,0 kg digantungkan di ujung sebuah tali yang terhubung dengan sebuah katrol bermassa M = 3,0 kg dan berjari-jari R = 0,25 m. Benda pada mulanya di tahan berada pada ketinggian 6,0 m kemudian dilepaskan sehingga benda mengalami gerak jatuh bebas, sedangkan katrol merupakan silinder pejal yang dapat berputar secara vertikal seperti yang ditunjukkan pada gambar di bawah ini

Tentukan :

a) besar tegangan tali

b) percepatan benda

pembahasan soal:

2) dua buah balok masing-masing bermassa mA = 2 kg dan mB = 3 kg dihubungkan dengan sebuah tali (massa diabaikan) melalui sebuah katrol (jari-jari R = 20 cm dan momen inersia I = 0,5 kgm²) seperti yang terlihat pada gambar di bawah ini

Kedua balok bergerak dengan kecepatan v dan balok bergerak tanpa ada gesekan dengan meja. Tentukan percepatan linier kedua benda!

pembahasan soal:

Sistem bidang miring

Ketika sebuah benda bergerak pada bidang miring (naik atau turun) pertama yang harus dikenali adalah apakah bendanya bergerak translasi saja, bergerak rotasi saja, atau keduanya secara bersamaan (menggelinding). Ketika benda tersebut bergerak menggelinding maka akan memiliki dua jenis energi kinetik yakni energi kinetik translasi dan energi kinetik rotasi.

Tips :

Gunakan hukum kekekalan energi mekanik dengan memperhatikan energi kinetik rotasinya
Perhatikan bentuk benda yang menggelinding, karena mempengaruhi persamaan momen inersianya
Perhatikan baik-baik persamaannya sebelum menghitung

Contoh

Sebuah silinder pejal menggelinding menuruni suatu permukaan miring dengan sudut kemiringan terhadap horizontal (θ = 37⁰) seperti yang terlihat pada gambar di bawah ini

Tentukan percepatan yang di alami benda tersebut!

pembahasan soal:

Penggabungan dua roda

Penggabungan dua roda adalah apabila ada dua roda (biasanya piringan) sama-sama berputar atau salah satu diam kemudian disatukan maka akan membentuk suatu sistem baru dengan momen inersia yang berbeda dan kecepatan sudut yang berbeda tapi momentum sudutnya tetap, jadi berlaku hukum kekekalan momentum sudut.

Tips :

Perhatikan awah kedua roda, karena momentum sudut merupakan besaran vektor jadi arahnya juga diperhitungkan dalam penyelesaian soal.
Dua roda yang digabung menjadi satu mirip dengan tumbukan tak lenting sama sekali, karena setelah bersatu keduanya bergerak bersama-sama

Contoh :

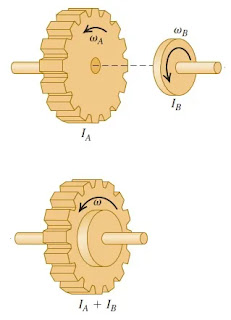
Roda A pada gambar memiliki massa 2,0 kg dan jari-jari 0,2 m serta kecepatan sudut awal 50 rad/s. roda 1 kemudian dikopel (satu poros) dengan roda B yang memiliki massa 4,0 kg, jari-jari 0,1 m dan kecepatan sudut awal 200 rad/s (gambar atas). Jika roda dianggap sebagai silinder pejal tentukan kecepatan sudut akhir setelah kedua roda tersebut disatukan! (gambar bawah)

pembahasan soal:

demikian penjelasan terkait dengan materi fisika kelas 11 : Dinamika rotasi, semoga bermanfaat bagi para pembaca. Agar lebih memahami materi ini silahkan klik latihan soal fisika materi : dinamika rotasi, disana ada beberapa contoh soal yang juga bisa dijadikan refrensi dengan penjelasan yang lengkap.

Sumber :

Homer, D., Jones, M. B. 2014 edition Phycics course companion. Oxford University press. 2014

Resnick, R., Halliday, D., Walker, J. Fundamentals of Physics, 10th ed., John Wiley & Sons, Inc. 2014

Serway, R. A., Faughn, J. S. Holt Physics. Holt. 2006

Wolfson, R. Essential university physics 2nd ed. Pearson education, Inc.2012

Young, H. D., Freedman, R. A. Sears ana Zemansky’s university physics : with modern physics 13th ed., Pearson education, Inc.2012

Rabu, 22 Juli 2020

Kupas tuntas! materi dinamika rotasi (fisika kelas 11)

Dinamika Rotasi

Torsi

Momen Inersia

Momentum Sudut

Energi kinetik rotasi

Analisis dinamika rotasi

2 komentar:

Halaman