Salah satu materi fisika kelas 11 adalah tentang dinamika rotasi, banyak siswa yang merasa kesulitan untuk mengerjakan soal tentang dinamika rotasi ini terutama terkait dengan hubungan torsi dengan gerak menggelinding, menentukan momen inersia, atau energi kinetik benda saat menggelinding. Berikut ini adalah beberapa contoh latihan soal materi fisika kelas 11 tentang dinamika rotasi lengkap dengan pembahasannya, dapat juga digunakan sebagai refrensi untuk soal ulangan harian. Semoga bisa membantu dan selamat menikmati
Tips :
ketentuan untuk momen gaya yang searah jarum jam bernilai negatif dan untuk momen gaya berlawanan arah jarum jam bernilai positif.
Soal Pilihan Ganda
Soal nomor 1
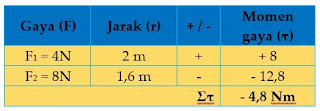
Sebuah tongkat panjang 2 meter tak bermassa dipasang pada sebuah engsel. Dua buah gaya masing-masing F1 = 4N dan F2 = 8N bekerja pada tongkat seperti pada gambar di bawah. Besar momen gaya dan arah putaran pada batang adalah ...
B. 4,8 Nm berlawanan arah jarum jam
C. 8,0 Nm searah jarum jam
D. 8,0 Nm berlawanan arah jarum jam
E. 12,8 Nm searah jarum jam
Kunci Jawaban : “B”
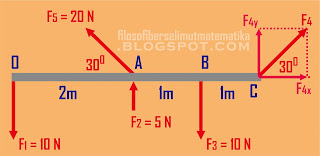
Sebuah batang AC panjangnya 4 m. Bila OA = 2 m, AB = BC = 1 m, dan massa batang
diabaikan, maka besar momen gaya pada poros A adalah ....
A. 30 Nm searah jarum jam
B. 30 Nm berlawanan arah jarum jam
C. 35 Nm searah jarum jam
D. 35 Nm berlawanan arah jarum jam
E. 40 Nm searah jarum jam
Kunci jawaban : “B”
Resultan momen gaya pada poros di titik perpotongan diagonal bujursangkar adalah ....
A. 0,12 N.m
B. 0,50 N.m
C. 0,75 N.m
D. 1,25 N.m
E. 1,75 N.m
Kunci jawaban : “C”
A. 0,125
B. 0,225
C. 1,115
D. 1,250
E. 1,500
Kunci jawaban : “D”
pembahasan soal nomor 1:
Soal nomor 2
perhatikan gambar berikut!
perhatikan gambar berikut!
A. 30 Nm searah jarum jam
B. 30 Nm berlawanan arah jarum jam
C. 35 Nm searah jarum jam
D. 35 Nm berlawanan arah jarum jam
E. 40 Nm searah jarum jam
Kunci jawaban : “B”
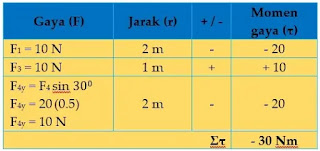
pembahasan soal nomor 2:
Soal nomor 3
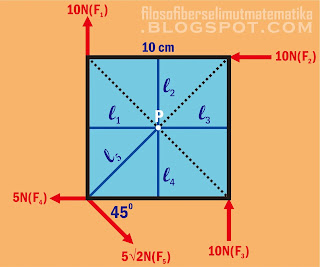
Lima gaya bekerja pada bujursangkar dengan sisi 10 cm seperti ditunjukkan pada gambar berikut:
Lima gaya bekerja pada bujursangkar dengan sisi 10 cm seperti ditunjukkan pada gambar berikut:
A. 0,12 N.m
B. 0,50 N.m
C. 0,75 N.m
D. 1,25 N.m
E. 1,75 N.m
Kunci jawaban : “C”
pembahasan soal nomor 3:
Soal nomor 4
perhatikan gambar berikut!
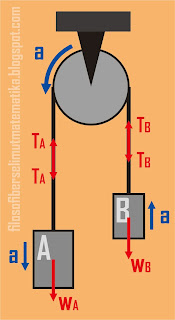
massa A = 4 kg, massa B = 3 kg dan massa katrol 2 kg. Katrol terbuat dari silinder pejal dan katrol ikut berputar dengan tali. Jika g = 10 m/s2, maka percepatan benda A adalah … .m/s2perhatikan gambar berikut!
A. 0,125
B. 0,225
C. 1,115
D. 1,250
E. 1,500
Kunci jawaban : “D”
pembahasan soal nomor 4:
Soal nomor 5
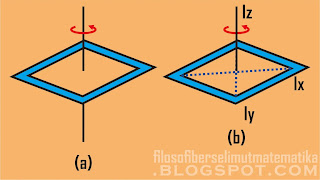
Tiga partikel identik diikat bermassa m ke ujung-ujung sebuah segitiga siku-siku sama kaki oleh batang-batang penghubung tak bermassa. Kedua sisi yang sama memiliki panjang a. momen inersia benda tegar ini untuk sumbu rotasi berhimpit pada sisi miringnya adalah ....
A. ¼ ma2
B. ½ ma2
C. ¾ ma2
D. ma2
E. 3/2 ma2
Kunci jawaban :”B”
Tiga partikel identik diikat bermassa m ke ujung-ujung sebuah segitiga siku-siku sama kaki oleh batang-batang penghubung tak bermassa. Kedua sisi yang sama memiliki panjang a. momen inersia benda tegar ini untuk sumbu rotasi berhimpit pada sisi miringnya adalah ....
A. ¼ ma2
B. ½ ma2
C. ¾ ma2
D. ma2
E. 3/2 ma2
Kunci jawaban :”B”
pembahasan soal nomor 5:
Soal nomor 6
perhatikan gambar berikut!
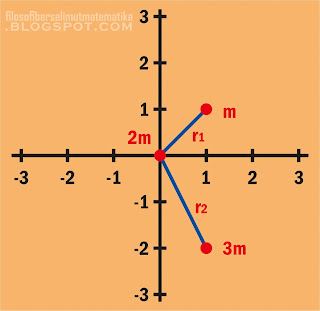
Tentukan momen inersia sistem partikel di atas, jika sistem diputar dengan poros di pusat koordinat (0,0)perhatikan gambar berikut!
A. 4m
B. 6m
C. 11m
D. 13m
E. 17m
Kunci jawaban: “E”
pembahasan soal nomor 6:
Soal nomor 7
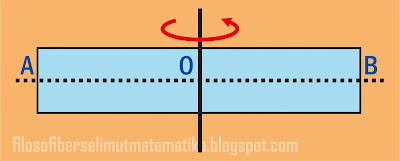
Batang AB bermassa 2 kg diputar melalui titik A ternyata momen inersianya 8 kgm2.
Bila diputar melalui titik pusat O (OA = OB), momen inersianya menjadi ... kgm2Batang AB bermassa 2 kg diputar melalui titik A ternyata momen inersianya 8 kgm2.
A. 2
B. 4
C. 8
D. 12
E. 16
Kunci jawaban : “A”
pembahasan soal nomor 7:
Soal nomor 8
perhatikan gambar berikut!
Sebuah cakram melingkar homogen dengan jari-jari R bermassa M berputar dengan poros melalui pusat cakram dan tegak lurus terhadap bidang memiliki momen inersia I0 = ½ MR2. Suatu lubang dipotong dalam cakram seperti ditunjukkan dalam diagram. Momen inersia yang dihasilkan benda terhadap sumbu seperti pada gambar adalah ....perhatikan gambar berikut!
A. (15/32) MR2
B. (13/32) MR2
C. (3/8) MR2
D. 9/32 MR2
E. (15/16) MR2
Kunci jawaban : “B”
pembahasan soal nomor 8:
Soal nomor 9
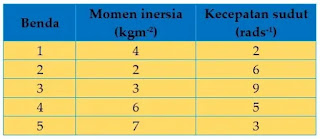
perhatikan tabel berikut!
Momentum sudut terbesar ditunjukkan
oleh benda ....perhatikan tabel berikut!
A. 1
B. 2
C. 3
D. 4
E. 5
Kunci jawaban : “D”
pembahasan soal nomor 9:
Soal nomor 10
Seorang penari berputar di atas lantai dasar yang gesekannya diabaikan. Dalam posisi tangan dan kaki tidak dibentangkan momen inersia I dan kecepatan sudutnya 2,4 rad/s. Kemudian kedua tangan dan salah satu kaki dibentangkan mendatar hingga momen inersianya 1,6 I. Maka selama 8 sekon penari tersebut melakukan putaran sebanyak … .
A. 1,5 kali
B. 3 kali
C. 6 kali
D. 12 kali
E. 24 kali
Kunci jawaban : “C”
Seorang penari berputar di atas lantai dasar yang gesekannya diabaikan. Dalam posisi tangan dan kaki tidak dibentangkan momen inersia I dan kecepatan sudutnya 2,4 rad/s. Kemudian kedua tangan dan salah satu kaki dibentangkan mendatar hingga momen inersianya 1,6 I. Maka selama 8 sekon penari tersebut melakukan putaran sebanyak … .
A. 1,5 kali
B. 3 kali
C. 6 kali
D. 12 kali
E. 24 kali
Kunci jawaban : “C”
pembahasan soal nomor 10:
Soal nomor 11
Seorang penari berdiri di atas lantai es licin dan berputar di tempatnya seperti pada gambar
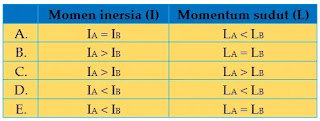
Seorang penari berdiri di atas lantai es licin dan berputar di tempatnya seperti pada gambar
Mula-mula penari tersebut berputar dengan menyilangkan kedua tangan di dadanya (gambar A). kemudian penari tersebut kembali berputar sambil merentangkan kedua tangannya (gambar B). Pernyataan pada tabel di bawah ini yang benar berkaitan dengan kedua keadaan penari di atas adalah ....
Kunci jawaban : “E”
pembahasan soal nomor 11:
Soal nomor 12
Pada saat piringan A berotasi 120 rpm (gambar 1), piringan B diletakkan di atas piringan A (gambar 2) sehingga kedua piringan berputar dengan poros yang sama.
Massa piringan A = 100 gram dan massa piringan B = 300 gram, sedangkan jari-jari piringan A = 50 cm dan jari-jari piringan B = 30 cm. jika momen inersia piringan adalah ½ m.R2, maka besar kecepatan sudut kedua piringan pada waktu berputar bersama-sama adalah ....Pada saat piringan A berotasi 120 rpm (gambar 1), piringan B diletakkan di atas piringan A (gambar 2) sehingga kedua piringan berputar dengan poros yang sama.
A. 0,67 π rad.s-1
B. 0,83 π rad.s-1
C. 1,92 π rad.s-1
D. 4,28 π rad.s-1
E. 5,71 π rad.s-1
Kunci jawaban : “C”
pembahasan soal nomor 12:
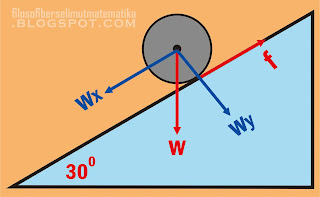
Bola pejal massa 3,5 kg menggelinding tanpa selip sepanjang bidang miring dengan sudut kemiringan 300. Jika percepatan gravitasi 10 m/s2, gaya gesekan antara bidang dengan bola adalah ...
A. 1 N
B. 2 N
C. 3 N
D. 4 N
E. 5 N
Kunci jawaban: “E”
A. 1 N
B. 2 N
C. 3 N
D. 4 N
E. 5 N
Kunci jawaban: “E”
pembahasan soal nomor 13:
Sebuah silinder pejal homogen dengan jari - jari 20 cm dan massa 2 kg yang berada di puncak bidang miring menggelinding meluncur menuruni bidang seperti pada gambar. Kelajuan benda saat tiba di dasar bidang miring adalah …..
A. 2√4 m/sB. 2√5 m/s
C. √30 m/s
D. √40 m/s
E. 30 m/s
Kunci jawaban: “A”
pembahasan soal nomor 14:
Sebuah bola pejal berada di atas sebuah lantai, lalu bola didorong dengan gaya F. Perbandingan percepatan yang dialami oleh bola ketika bola tersebut tergelincir dan ketika bola menggelinding adalah ....
A. 3/2
B. 2/3
C. 7/5
D. 5/7
E. 8/5
Kunci jawaban : “C”
A. 3/2
B. 2/3
C. 7/5
D. 5/7
E. 8/5
Kunci jawaban : “C”
pembahasan soal nomor 15:
Soal nomor 16
Sebuah bol pejal I (2/5 mR2) bermassa 2 kg menggelinding pada bidang datar seperti ditunjukkan oleh gambar di bawah.
Pada saat kecepatan linier bola v = 10 m·s–1, maka energi kinetik total bola adalah ....Sebuah bol pejal I (2/5 mR2) bermassa 2 kg menggelinding pada bidang datar seperti ditunjukkan oleh gambar di bawah.
A. 28 J
B. 70 J
C. 140 J
D. 280 J
E. 1400 J
Kunci jawaban: “C”
pembahasan soal nomor 16:
Soal Esai
Soal nomor 1
Sebuah bingkai persegi yang terbuat dari empat batang tipis yang masing-masing memiliki panjangnya L dan bermassa m. tentukan momen inersia bingkai tersebut jika diputar dengan sumbu poros seperti gambar di bawah ini!
Sebuah bingkai persegi yang terbuat dari empat batang tipis yang masing-masing memiliki panjangnya L dan bermassa m. tentukan momen inersia bingkai tersebut jika diputar dengan sumbu poros seperti gambar di bawah ini!
pembahasan soal nomor 1:
Soal nomor 2
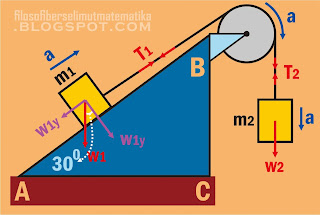
Dua benda masing-masing bermassa m1 = 4 kg dan m2 = 4 kg dihubungkan dengan katrol yang bermassa 4 kg seperti tampak pada gambar di bawah ini.
Jika permukaan bidang AB licin, tentukan percepatan benda m1 dan m2 !
Dua benda masing-masing bermassa m1 = 4 kg dan m2 = 4 kg dihubungkan dengan katrol yang bermassa 4 kg seperti tampak pada gambar di bawah ini.
pembahasan soal nomor 2:
Soal nomor 3
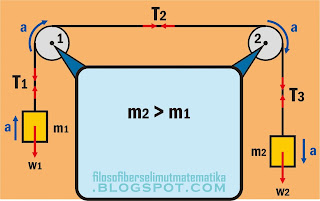
Dua buah balok m1 dan m2 saling dihubungkan dengan seutas tali yang dilewatkan pada dua buah katrol yang identik dengan momen inersia I seperti pada gambar berikut ini.
Tentukan percepatan kedua benda
Dua buah balok m1 dan m2 saling dihubungkan dengan seutas tali yang dilewatkan pada dua buah katrol yang identik dengan momen inersia I seperti pada gambar berikut ini.
pembahasan soal nomor 3:
Soal nomor 4
perhatikan gambar berikut!
Roda A pada gambar memiliki massa 2,0 kg dan jari-jari 0,20 m, serta kecepatan sudut awal 50 rad/s (kira-kira 500 rpm). Roda A dikopel (satu poros) dengan keping B yang memiliki massa 4,0 kg, jari-jari 0,10 m, dan kecepatan sudut awal 200 rad/s (gambar atas). tentukan kecepatan sudut akhir bersama ω setelah keduanya didorong sehingga bersentuhan (gambar bawah). Apakah energi kinetik kekal selama proses ini?
perhatikan gambar berikut!
pembahasan soal nomor 4:
Soal nomor 5
Sebuah silinder pejal yang mula-mula diam bergerak menggelinding dari puncak sebuah bidang miring. saat berada di dasar bidang miring kelajuannya 4 m/s. tentukan ketinggian bidang miring tersebut!
Sebuah silinder pejal yang mula-mula diam bergerak menggelinding dari puncak sebuah bidang miring. saat berada di dasar bidang miring kelajuannya 4 m/s. tentukan ketinggian bidang miring tersebut!
pembahasan soal nomor 5:
demikian soal-soal yang dapat digunakan untuk mempelajari materi fisika kelas 11 :dinamika rotasi. Terima kasih sudah mampir di blog ini
baca juga :
















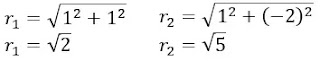










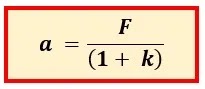





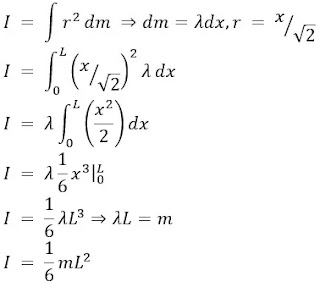

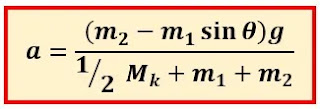


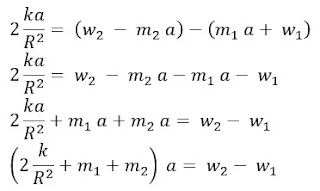






Tidak ada komentar:
Posting Komentar