Daftar IsiMateri fisika kelas 10 : vektor (Lengkap dengan contoh soal)
Gambar 1. Papan penunjuk jalan
Gambar 1 di atas merupakan salah satu tanda yang sering kita lihat ketika
bepergian yang digunakan agar orang yang melintasi jalan tersebut tidak
tersesat dan bisa sampai ke tujuan dengan benar. Papan tersebut pada dasarnya
menunjukkan arah ke mana kita harus pergi, mengetahui arah merupakan sesuatu
yang sangat penting dalam kehidupan sehari-hari, bayangkan Orang yang sedang
bepergian akan kesulitan menuju tempat tujuannya jika tidak ada penunjuk jalan
yang menunjukkan arahnya. Dalam pembelajaran fisika materi tentang arah
termasuk dalam materi kelas 10 yakni “vektor” membahas tentang besaran-besaran
fisika yang memiliki arah. Pentingnya “arah” memang tak dapat dipungkiri lagi
bagi kehidupan sehari-hari tanpa adanya arah kita akan kesulitan untuk
mengetahui posisi kita dan posisi tujuan kita, dengan mengetahui arah kita
tidak akan tersesat. bahkan jika tidak ada arah mungkin tidak akan ada yang
namanya GPS “global positioning system” karena pada dasarnya GPS
menggunakan sistem koordinat untuk posisi kita dan posisi tujuan sehingga
dapat menemukan arah yang tepat untuk menuju lokasi tujuan tersebut. Oleh
karena itu setelah mengetahui manfaat “arah” dalam kehidupan sehari-hari,
silahkan mempelajari materi berikut ini.
Karakteristik Vektor
Tidak semua besaran di fisika dapat disebut dengan besaran vektor ada beberapa
karakteristik dari besaran vektor tersebut yang dapat ditinjau dari:
pengertian vektor, menulis dan menggambar vektor, vektor satuan.
Pengertian vektor
Vektor merupakan besaran yang memiliki nilai dan arah (berbeda dengan besaran
skalar yang hanya memiliki nilai saja). Cara menentukan suatu besaran fisika
termasuk besaran vektor atau bukan sebenarnya cukup sederhana yakni dengan
memberikan kalimat tanya “kemana atau dimana” pada besaran tersebut jika
besaran tersebut cocok (tidak asing terdengar) maka besaran tersebut termasuk
besaran vektor, contohnya “kemana ia akan pindah rumah?”, kalimat tanya ini
sebenarnya menanyakan arah dan posisi dari tujuan pindah dan sering kita
dengar, sehingga perpindahan termasuk besaran vektor. misalkan ada pertanyaan
“kemana jaraknya rumahmu ke sekolah?” kalimat tanya ini terdengar asing,
karena memang tidak cocok antara kalimat tanya kemana dengan besaran jarak,
besaran jarak lebih cocok menggunakan kalimat tanya berapa, sehingga jarak
termasuk besaran skalar.
Perpindahan dan jarak memang sering digunakan dalam fisika, tidak sedikit
siswa yang biasanya kesulitan membedakan antara perpindahan dan jarak karena
di beberapa kasus sering terjadi jarak = perpindahan. Untuk dapat membedakan
antara jarak dan perpindahan perhatikan gambar berikut.
Gambar 2. Sebuah partikel bergerak dari A ke B dengan lintasan yang
ditempuh sesuai dengan garis merah
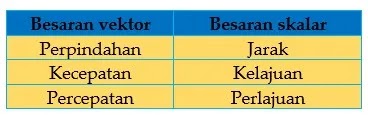
Berdasarkan gambar 2 di atas, jarak merupakan panjang lintasan yang ditempuh (garis merah putus-putus) sedangkan perpindahan merupakan jarak terpendek dari posisi awal (A) ke posisi akhir (B) yang ditunjukkan dengan garis biru dengan arah 600 terhadap garis horizontal. Berdasarkan ilustrasi di atas terlihat perbedaan yang cukup signifikan antara jarak dan perpindahan. Beberapa besaran lain yang sering ditemui di fisika yang memiliki kemiripan antara besaran skalar dan vektor antara lain dapat dilihat pada tabel di bawah ini
Penting!
Arah dalam besaran vektor dapat dinyatakan dalam berbagai cara, antara lain sudut, arah mata angin, atas, bawah, ke kiri, ke kanan, dll. Arah vektor juga menentukan ketika dilakukan perhitungan matematis beberapa vektor, vektor yang searah dijumlahkan, sedangkan vektor yang berlawanan arah akan dikurangi.
Arah dalam besaran vektor dapat dinyatakan dalam berbagai cara, antara lain sudut, arah mata angin, atas, bawah, ke kiri, ke kanan, dll. Arah vektor juga menentukan ketika dilakukan perhitungan matematis beberapa vektor, vektor yang searah dijumlahkan, sedangkan vektor yang berlawanan arah akan dikurangi.
Menulis dan menggambar vektor
Telah dijelaskan sebelumnya bahwa besaran vektor adalah besaran yang memiliki
nilai (besar) dan arah sehingga memiliki cara tersendiri dalam penulisan
maupun penggambarannya. Cara penulisan besaran vektor sedikit berbeda dengan
penulisan besaran skalar. Misalkan kita akan menulis sebuah vektor “A” pada
beberapa buku terdapat beberapa cara dalam menuliskan besaran vektor
yakni
- Simbol vektor di cetak tebal Sehingga penulisan vektor “A” adalah “A”
- Simbol vektor di cetak tebal dan miring Sehingga penulisan vektor “A” adalah “A”
- Simbol vektor di cetak tebal, miring dan diberi tanda arah di atasnya Sehingga penulisan vektor “A” adalah “\vec{\mathbit{A}}”
- Simbol vektor di beri tanda arah di atasnya Sehingga penulisan vektor “A” adalah “\vec{A}”
Cara penulisan seperti pada point 1 sampai 3 biasanya digunakan pada buku-buku
pelajaran karena ada fasilitas untuk bold dan italic sedangkan
jika menulis di papan tulis atau buku tulis dapat menggunakan cara ke 4.
Besarnya (nilai) suatu besaran vektor dapat dituliskan dengan cara memberikan
tanda “mutlak” seperti ini “∣A∣” atau ditulis biasa seperti ini “A”.
Besaran vektor biasanya digambarkan dengan anak panah dengan panjang anak
panah menggambarkan besar vektor dan arah anak panah menggambarkan arah
vektor. perhatikan gambar berikut.
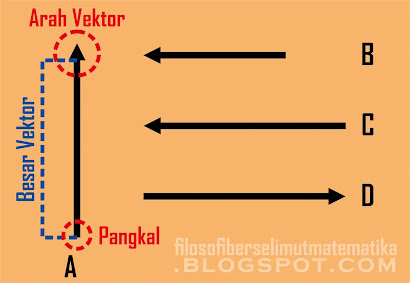
Gambar 3. Beberapa gambar vektor
Berdasarkan gambar 3 di atas terlihat bagian-bagian vektor dari sebuah anak
panah pada vektor A, perhatikan gambar vektor B dan vektor
C memiliki arah yang sama (ke kiri) tapi vektor C lebih besar
dari pada vektor B (ditunjukkan dengan panjangnya yang berbeda),
sedangkan untuk vektor B dan vektor D memiliki besar yang sama
tetapi arahnya berlawanan (ditunjukkan oleh arah anak panah).
Komponen vektor dan vektor satuan
Komponen vektor merupakan salah salah satu cara yang digunakan untuk
mengalisis sebuah vektor dalam sistem koordinat (dalam kesempatan kali ini
digunakan sistem koordinat kartesian (x,y,z)) sehingga sebuah vektor
pada dasarnya memiliki komponen dalam arah sumbu x, sumbu
y maupun sumbu z. Misalkan untuk sistem koordinat
(x,y) dalam menentukan komponen suatu vektor menggunakan aturan
trigonometri sederhana (sinus, cosinus, tangen). Perhatikan gambar
berikut
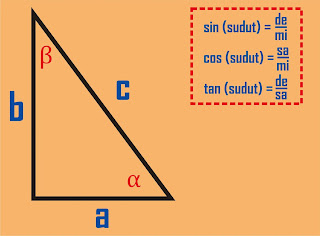
Gambar 4. Trigonometri untuk sinus, cosinus, tangen, pada segitiga siku-siku
Dengan menggunakan aturan trigonometri sederhana di atas, kita dapat
menentukan nilai sinus, cosinus, dan tangen untuk sudut α dan sudut β seperti
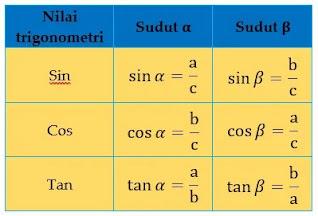
yang terlihat pada tabel berikut
Berdasarkan tabel di atas, jika kita perhatikan lebih jauh maka akan terlihat
pada dasarnya nilai tangen merupakan hasil pembagian antara nilai sinus dan
cosinusnya.
Menganalisis suatu vektor dengan menggunakan komponen vektor sangat penting
untuk dipahami, karena komponen vektor merupakan salah satu materi dasar yang
nantinya akan terus digunakan pada materi-materi fisika selanjutnya. Misalkan
sebuah vektor A digambarkan dalam sistem koordinat kartesian
(x,y) seperti terlihat pada gambar berikut
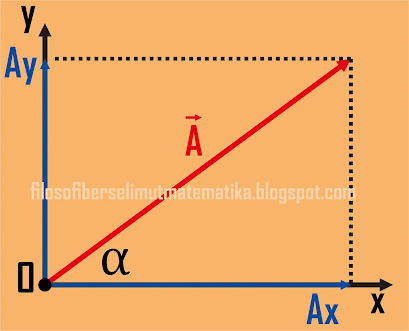
Gambar 5. Sebuah vektor A digambarkan dalam bidang x – y dengan membentuk
sudut α terhadap sumbu x
Vektor A yang digambarkan membentuk sudut α terhadap sumbu x,
vektor A tersebut, dapat di proyeksikan terhadap sumbu x dan
sumbu y sehingga memiliki komponen vektor Ax dan Ay yang dapat
ditentukan dengan trigonometri di atas seperti berikut.
Ax = A cos α
Ay = A sin α
Kedua komponen vektor di atas bernilai positif karena arahnya sesuai dengan arah sumbu x positif dan arah sumbu y positif, selain itu komponen vektor juga dapat bernilai negatif jika arahnya sesuai dengan arah sumbu x negatif dan arah sumbu y negatif (perhatikan arah tanda panahnya, untuk sumbu x ke kanan bernilai positif dan ke kiri bernilai negatif. Untuk sumbu y ke atas bernilai positif dan ke bawah bernilai negatif). Hubungan antara vektor dan komponen vektor seperti pada gambar di atas secara vektor dapat ditulis A = Ax + Ay.
Berdasarkan komponen vektor kita dapat juga mengetahui besar dan arah vektor utamanya, misalkan untuk vektor komponen Ax dan Ay di atas dapat kita tentukan besar dan arah vektor A (arah ditunjukkan dengan besar sudutnya) sebagai berikut.
Ax = A cos α
Ay = A sin α
Kedua komponen vektor di atas bernilai positif karena arahnya sesuai dengan arah sumbu x positif dan arah sumbu y positif, selain itu komponen vektor juga dapat bernilai negatif jika arahnya sesuai dengan arah sumbu x negatif dan arah sumbu y negatif (perhatikan arah tanda panahnya, untuk sumbu x ke kanan bernilai positif dan ke kiri bernilai negatif. Untuk sumbu y ke atas bernilai positif dan ke bawah bernilai negatif). Hubungan antara vektor dan komponen vektor seperti pada gambar di atas secara vektor dapat ditulis A = Ax + Ay.
Berdasarkan komponen vektor kita dapat juga mengetahui besar dan arah vektor utamanya, misalkan untuk vektor komponen Ax dan Ay di atas dapat kita tentukan besar dan arah vektor A (arah ditunjukkan dengan besar sudutnya) sebagai berikut.
Telah dijelaskan sebelumnya bahwa komponen vektor ditinjau dari sistem
koordinat kartesian, masing-masing sumbu koordinat memiliki ciri khas
tersendiri yang disebut dengan vektor satuan, seperti yang terlihat pada tabel
berikut
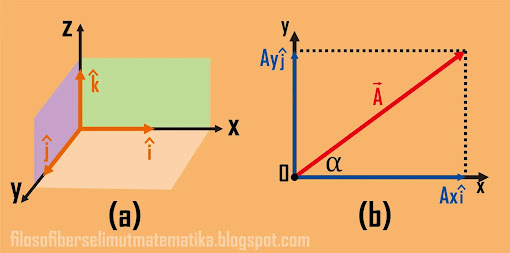
Arah vektor satuan ini sesuai dengan arah sumbunya, perhatikan gambar berikut
Gambar 6. (a) arah komponen vektor pada koordinat kartesian, (b) proyeksi
vektor A terhadap sumbu x dan sumbu y dengan vektor satuan
Vektor satuan juga menunjukkan bahwa suatu besaran adalah besaran vektor dalam
komponen sumbu tertentu, sehingga jika ada penulisan menggunakan vektor satuan
maka besaran tersebut merupakan besaran vektor dan penulisan Ax dan Ay
menyatakan besar (nilai dari besarannya), sehingga dengan menggunakan vektor
satuan vektor A pada gambar 6b dapat ditulis
Contoh soal
1) Seorang pejalan kaki berjalan sejauh 5,0 km ke timur dan 12,0 km ke selatan. Tentukan besar dan arah perpindahan pejalan kaki tersebut.
1) Seorang pejalan kaki berjalan sejauh 5,0 km ke timur dan 12,0 km ke selatan. Tentukan besar dan arah perpindahan pejalan kaki tersebut.
pembahasan soal:
Sebuah bagian dari mesin dinaikkan melalui papan miring dan menempuh jarak
sejauh d = 12 m dengan papan membentuk sudut θ = 300
terhadap lantai. Tentukan berapa jauh perpindahan yang dilakukan oleh bagian
mesin tersebut secara vertikal dan horizontal!
pembahasan soal:
Resultan Vektor
Resultan vektor merupakan cara untuk menentukan total vektor dari beberapa
vektor. Beberapa buku mengatakan bahwa resultan vektor sama dengan
penjumlahan vektor, menggunakan istilah ini lebih riskan dan berpotensi
terjadi miskonsepsi dalam mengerjakan soal. Hal ini dikarenakan kata
penjumlahan merujuk pada “ditambah” jadi dianggap penjumlahan vektor adalah
semua vektor ditambah saja, padahal vektor merupakan besaran yang memiliki
nilai dan arah jadi ketika ingin mencari total vektor perlu dipertimbangkan
arahnya, jika vektor-vektornya searah maka akan dijumlah, tapi jika
berlawanan arah akan dikurangi, hal ini akan mempengaruhi hasil perhitungan
pada akhirnya. Oleh karena itu saya lebih suka menggunakan resultan vektor
sebagai total vektor bukan penjumlahan vektor karena perlu mempertimbangkan
arahnya.
Resultan vektor dapat ditentukan dengan dua metode yakni dengan metode
melukis atau menggambarnya dan dengan metode analitis
Resultan vektor dengan metode melukis
Menentukan resultan vektor dengan metode melukis ini terbagi menjadi dua
cara lagi yakni metode poligon dan metode jajargenjang.
Konsep :
Dalam menggunakan metode melukis persamaan matematis dari resultan vektor
akan mempengaruhi gambar dan hasilnya, misalkan dua vektor A dan
B akan ditentukan resultan vektor dengan persamaan vektor C =
A + B dan dengan persamaan C = A – B akan
menghasilkan gambar yang berbeda dan hasil yang berbeda, karena vektor
B tidak sama dengan vektor -B yang membedakan adalah arahnya
tanda negatif (-) menunjukkan arahnya berlawanan dengan arah vektor semula,
sehingga dalam menggambarnya arahnya perlu dibalik terlebih dahulu.
Perhatikan gambar berikut
Gambar 7. Perbedaan antara vektor B dengan vektor -B
Metode poligon
Prinsip resultan vektor dengan menggunakan metode poligon ini pada dasarnya
adalah “meneruskan” vektor-vektor yang akan ditentukan resultannya kemudian
mencari jarak terdekat dari posisi awal ke posisi akhirnya (ditarik garis
lurus). Meneruskan yang dimaksud disini adalah menghubungkan ujung (arah
panah) vektor pertama dengan pangkal vektor kedua, ujung vektor kedua dengan
pangkal vektor ketiga begitu seterusnya. Perhatikan gambar berikut
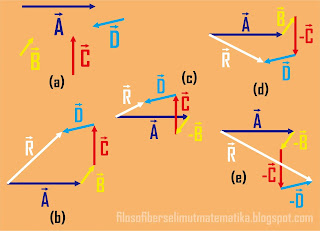
Gambar 8. Menentukan resultan vektor dengan metode poligon
Gambar 8 merupakan contoh cara menentukan resultan vektor dengan metode
poligon. Mula-mula ada 4 vektor masing-masing adalah A, B,
C, dan D yang memiliki besar dan arah seperti ditunjukkan oleh
gambar 8a. gambar 8b menunjukkan resultan vektor dengan persamaan R =
A + B + C + D, tidak ada vektor yang bernilai
negatif (berbalik arah), gambar 8c menunjukkan resultan vektor dengan
persamaan R = A - B + C + D, vektor
B bernilai negatif karena arahnya berlawanan dengan arah mula-mula,
gambar 8d menunjukkan resultan vektor dengan persamaan R = A +
B - C + D, vektor C bernilai negatif karena
arahnya berlawanan dengan arah mula-mula, gambar 8e menunjukkan resultan
vektor dengan persamaan R = A - B - C –
D, selain vektor A, semua vektor bernilai negatif karena
arahnya berlawanan dengan arah mula-mula.
Jurus jitu
Untuk tipe soal yang menggunakan metode poligon, jika merasa kesulitan dengan cara seperti di atas, kalian boleh menggambar semua vektor dimulai dari titik koordinat (0,0) kemudian mencari resultan dalam arah sumbu x dan sumbu y dan terakhir menentukan resultannya dengan persamaan phytagoras. Silahkan dilihat soal nomor 2 disini.
Jurus jitu
Untuk tipe soal yang menggunakan metode poligon, jika merasa kesulitan dengan cara seperti di atas, kalian boleh menggambar semua vektor dimulai dari titik koordinat (0,0) kemudian mencari resultan dalam arah sumbu x dan sumbu y dan terakhir menentukan resultannya dengan persamaan phytagoras. Silahkan dilihat soal nomor 2 disini.
Metode jajargenjang
Metode jajargenjang agak berbeda dengan metode poligon, jika pada metode
poligon meneruskan, maka pada metode jajarrgenjang vektor-vektor yang akan
dicari resultannya digambar dari titik awal yang sama, kemudian digandakan
sehingga membentuk bangun jajargenjang (sesuai dengan nama metodenya). Jarak
diagonal pada bangun jajargenjang yang terbentuk adalah resultan dari
vektor-vektor tersebut. metode jajargenjang ini lebih mudah digunakan
apabila ada dua vektor yang akan dicari resultannya. Berikut contoh
penggunaan metode jajargenjang
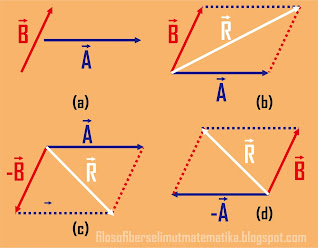
Gambar 9. Menentukan resultan vektor dengan metode jajargenjang
Gambar 9 merupakan contoh menentukan resultan vektor dengan metode
jajargenjang, misalkan mula-mula untuk vektor A dan B yang
terlihat seperti gambar 9a. gambar 9b merupakan resultan kedua vektor untuk
persamaan R = A + B, gambar 9c merupakan resultan kedua
vektor untuk persamaan R = A - B, gambar 9d merupakan
resultan kedua vektor untuk persamaan R = (-A) +
B.
Resultan vektor dengan metode analitis
Menentukan resultan vektor dengan metode analitis adalah bagaimana cara
menentukan resultan vektor dengan menggunakan persamaan-persamaan matematis.
Operasional matematis tetap berlaku saat menentukan resultan vektor,
beberapa di antaranya antara lain
Penjumlahan vektor berlaku sifat komutatif
Misalkan ada dua vektor a dan b untuk menentukan resultannya dengan
jumlahkan maka untuk menjumlahkannya bisa dilakukan dengan dua cara yakni
a + b atau b + a hal ini tidak akan mempengaruhi
hasil perhutingannya
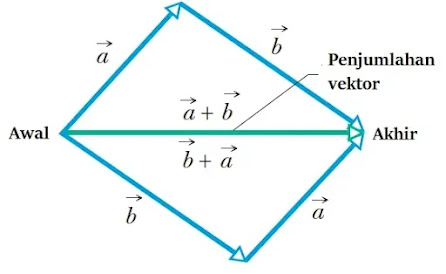
sifat komutatif ini juga bisa ditunjukkan dengan metode melukis seperti pada
gambar berikut
(Sumber: fundamentals of physics)
Penjumlahan vektor berlaku sifat asosiatif
Penjumlahan lebih dari dua vektor dapat dilakukan dengan cara
mengelompokkannya terlebih dahulu. Misalkan ada 3 vektor a, b,
dan c ingin ditentukan resultan vektornya dengan cara mengelempokkan
terlebih dahulu maka cara mengelempokkannya dapat dilakukan dengan dua cara
bisa (a+b) + c atau a+(b+c) hal
ini tidak akan mempengaruhi hasil perhitungannya.
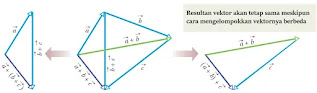
Sifat asosiatif ini bisa juga ditunjukkan dengan menggunakan metode melukis
seperti yang terlihat pada gambar berikut
Gambar 11. Tiga vektor a, b, dan c dapat
dikelompokkan dengan cara yang berbeda ketika ditambahkan (sifat
asosiatif)
(sumber: fundamentals of physic)
(sumber: fundamentals of physic)
Pengurangan vektor
Pengurangan vektor yang dimaksud disini bukan seperti pengurangan vektor
pada soal matematika biasa seperti 5 – 4, akan tetapi pengurangan vektor
disni terjadi karena arah dari vektor-vektornya berlawanan, jangan lupa
bahwa vektor merupakan besaran yang memiliki nilai dan arah, sehingga arah
dari sebuah vektor akan mempengaruhi persamaan matematis dari resultan
vektor. perhatikan gambar berikut
Gambar 12. Vektor b dan -b memiliki besar yang sama tapi
berlawanan arah
(sumber: fundamentals oh physics)
Vektor -b adalah sebuah vektor yang memiliki besar sama dengan vektor
b akan tetapi berlawanan arah dengan vektor b seperti yang
terlihat pada gambar 12 di atas, jika kedua vektor tersebut dijumlahkan maka
kita dapat menulis b + (-b) = 0, melukiskan resultan
vektor dalam bentuk negatif dapat dilakukan dengan dua cara seperti yang
terlihat pada gambar berikut!
Ingatlah!
berdasarkan penjelasan di atas, maka dapat mengetahui bahwa tanda negatif (-) dalam vektor bukan sekedar untuk mengurangi tapi tanda negatif juga menunjukkan arah vektor yang berlawanan.
Ingatlah!
berdasarkan penjelasan di atas, maka dapat mengetahui bahwa tanda negatif (-) dalam vektor bukan sekedar untuk mengurangi tapi tanda negatif juga menunjukkan arah vektor yang berlawanan.
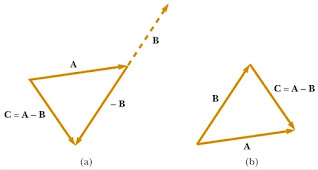
Gambar 13. Cara melukis resultan vektor untuk vektor bernilai negatif (a)
vektor -B merupakan kebalikan dari vektor B yang memiliki
besar sama tapi berlawanan arah, terapkan konsep metode poligon sehingga
kita kan mendapatkan persamaan C = A – B. (b) cara
kedua yakni dengan menggambar vektor B dari vektor A
(sumber: physics for scientist and engineers)
(sumber: physics for scientist and engineers)
Menentukan besar resultan dua vektor dengan aturan cos
Menentukan besar resultan dengan cara ini dapat digunakan apabila ada dua
vektor yang membentuk sudut apit tertentu. Perhatikan gambar berikut ini
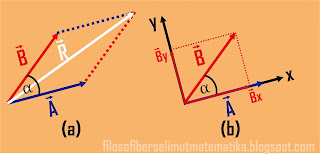
Gambar 14. Menentukan resultan dua vektor A dan B
Apabila terdapat dua vektor A dan B, membentuk sudut apit diantara keduanya sebesar α sehingga untuk menentukan resultan keduanya terlihat seperti gambar 14a (dengan menggunakan metode jajargenjang). Sekarang kita mencoba menentukan besar resultan vektor tersebut dengan cara membuat salah satu vektor sebagai sumbu x kemudian vektor lainnya diproyeksikan terhadap sumbu x (gambar 14b), maka besar resultannya dapat ditentukan dengan cara, Menentukan resultan masing-masing sumbu terlebih dahulu, beru kemudian dilanjutkan dengan rumus phytagoras
gambar 14a
Pada beberapa buku, aturan cosinus ditulis seperti di atas, padahal tidak
selalu seperti di atas bentuk persamaannya. Hal ini bergantung pada arah
vektor yang digambarkan. untuk lebih jelasnya perhatikan gambar berikut
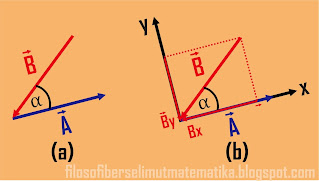
Gambar 15. Menentukan resultan dua vektor B dan A
Perbedaan antara gambar 15a dengan gambar 14a terletak pada arah vektor
B, sehingga memberikan dampak pada proyeksinya terhadap vektor
A yang terlihat pada gambar 15b, maka resultan vektornya dapat
ditentukan dengan cara yang sama untuk gambar 14 yakni
gambar 15a
gambar 15a
Perhatikan persamaan di atas, terlihat adanya perbedaan dengan persamaan
sebelumnya, hal ini menunjukkan bahwa ketika arah vektornya berubah, maka
persamaannya juga mengalami perubahan.
Resultan vektor komponen
Pada dasarnya untuk menentukan resultan vektor yang terdiri dari vektor
komponennya tidak jauh berbeda dengan menentukan resultan vektor seperti
biasa. Akan tetapi karena diketahui vektor komponennya (dalam sumbu
x dan sumbu y) maka operasional matematikanya harus sesuai,
untuk operasional penjumlahan (atau pengurangan) dikhususkan untuk vektor
komponen yang satu sumbu koordinat, sedangkan resultan vektor antara sumbu
x dan sumbu y dapat digunakan metode poligon, jajargenjang,
atau aturan cosinus.
Misalkan dua buah vektor masing-masing A = Axi +
Ayj dan B = Bxi + Byj, akan ditentukan besar resultannya maka yang harus dilakukan
adalah menjumlahkan masing-masing komponen vektornya secara terpisah seperti
berikut
R = A + B
R = (Ax + Bx)i + (Ay +
By)j
R = Rxi + Ryj (Rx =
Ax + Bx dan Ry = Ay +
By)
Besarnya resultan vektor (R) dan arahnya (α) dapat ditentukan dengan
cara
Hasil persamaan di atas sesuai dengan jika menentukan resultan vektor
menggunakan metode poligon seperti gambar berikut
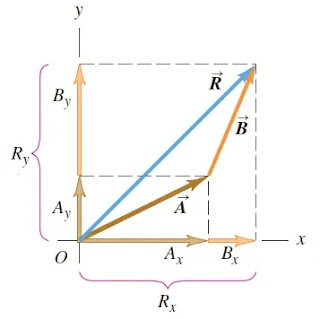
Gambar 16. Menentukan vektor resultan dari vektor A dan
B
(sumber: physics university)
Penjelasan di atas, juga berlaku jika vektor berada pada sumbu koordinat (x, y, z) misalkan dua buah vektor masing-masing A = Axi +
Ayj + Azk dan B = Bxi + Byj + Bzk, akan ditentukan
besar resultannya maka yang harus dilakukan adalah menjumlahkan
masing-masing komponen vektornya secara terpisah seperti berikut
R = A + B
R = (Ax + Bx)i + (Ay + By)j + (Az + Bz)k
R = Rxi + Rxj + Rzk (Rx = Ax + Bx , Ry = Ay + By dan Rz = Az + Bz)
Contoh Soal
1) dua buah vektor disajikan dalam unit vektor sebagai berikut!
a = (4 m)i – (3 m)j + (1 m)k
b = (-1 m)i + (1 m)j + (4 m)k
tentukan resultan vektornya untuk (a) a + b, (b) a - b, dan (c) vektor c jika a - b + c = 0
R = A + B
R = (Ax + Bx)i + (Ay + By)j + (Az + Bz)k
R = Rxi + Rxj + Rzk (Rx = Ax + Bx , Ry = Ay + By dan Rz = Az + Bz)
Contoh Soal
1) dua buah vektor disajikan dalam unit vektor sebagai berikut!
a = (4 m)i – (3 m)j + (1 m)k
b = (-1 m)i + (1 m)j + (4 m)k
tentukan resultan vektornya untuk (a) a + b, (b) a - b, dan (c) vektor c jika a - b + c = 0
pembahasan soal:
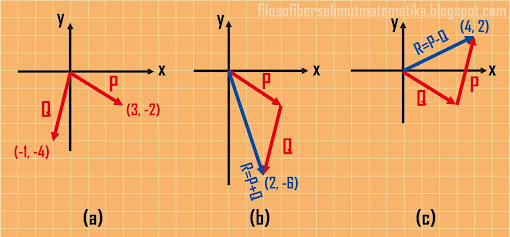
2) dua buah vektor masing-masing P = 3i – 2j dan
Q = –i – 4j dengan metode menggambar dan metode
analitis tentukan besar dan arah dari (a) R = P + Q,
(b) R = P – Q.
pembahasan soal:
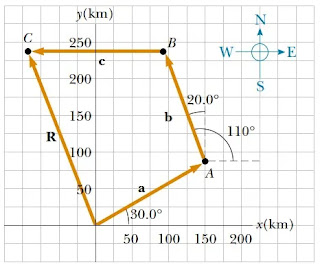
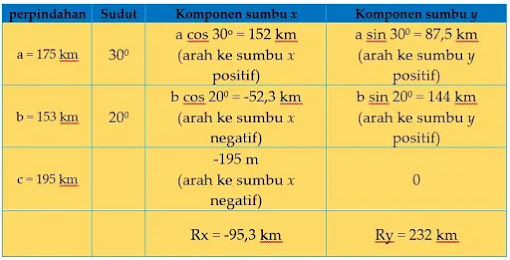
Jika pertama pesawat terbang mulai dari titik pusat koordinat (0,0) menuju
kota A yang berjarak 175 km dalam arah 300 ke timur laut,
kemudian terbang lagi 1530 ke arah 200 barat laut menuju kota B dan terkahir
terbang 195 km ke barat menuju kota C. Tentukan lokasi kota C relatif
terhadap titik awal!
pembahasan soal:
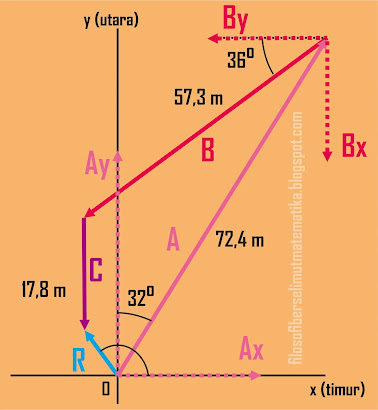
4) seorang pemburu harta karun membawa peta, meteran panjang, sekop, dan
kompas untuk mencari sebuah harta karun yang hilang. Ia mengikuti instruksi
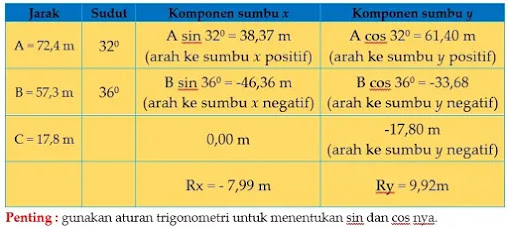
dan berjalan sejauh 72,4 m (320 ke arah timur laut) kemudian 57,3
m (360 ke arah barat daya) dan 17,8 m ke arah selatan kemudian
mulai menggali harta karun tersebut. berdasarkan ilustrasi di atas, tentukan
besar dan arah perpindahan yang dilakukan oleh pemburu harta karun tersebut
dari titik asal ke tempat harta karun ditemukan!
pembahasan soal:
Pengaruh perubahan sumbu koordinat terhadap vektor
Penjelasan yang telah dilakukan selama ini vektor dengan sumbu koordinat
yang tetap yakni garis horizontal sebagai sumbu x dan garis vertikal
sebagai sumbu y. Bagaimana jika suhu koordinat tidak tepat terhadap
garis vertikal dan garis horizontal? Atau ketika sumbu koordinatnya berputar
dengan sudut tertentu? Sekarang mari kita analisis untuk sumbu koordinat
yang tidak tepat di garis vertikal dan garis horizontal.
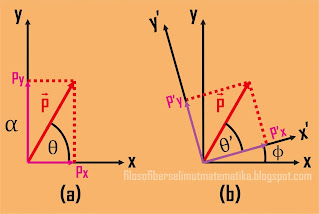
Gambar 17. (a) vektor P diproyeksi terhadap sumbu (x,y), (b) vektor
P diproyeksi terhadap sumbu (x’, y’) yang memiliki sudut sebesar ϕ
terhadap koordinat awal
Gambar 17a menunjukkan vektor P dan komponennya terhadap sumbu (x, y) yakni Pxi dan Pyj yang tegak lurus vertikal dan horizontal.
Jika kemudian sumbu koordinatnya diputar dengan sudut ϕ terhadap sumbu
x sehingga sumbu koordinatnya menjadi x’ dan y’ maka
vektor P memiliki komponen vektor yang baru yakni P’xi dan
P’yj. Kedua nilai komponen ini sama benarnya tergantung pada sumbu
koordinat yang dipakai, oleh karena itu dalam persamaan matematis dapat
ditulis sebagai berikut
Berdasarkan penjelasan di atas, maka dapat dikatakan bahwa kita dapat
memilih sumbu koordinat secara bebas, karena hubungan antar vektor tidak
bergantung pada lokasi asal atau sumbu koordinat tertentu.
Contoh soal
Perhatikan gambar berikut
Contoh soal
Perhatikan gambar berikut
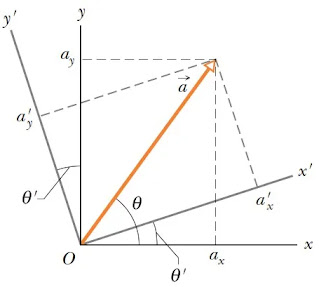
Sebuah vektor a yang besarnya 18 m memiliki arah sebesar θ
(θ=600) berlawanan arah jarum jam dengan sumbu +x. (a)
Tentukan vektor komponen ax dan ay (b) jika sumbu koordinat
diputar sebesar θ’ (θ’=150) maka tentukan vektor komponen
a’x dan a’y !
pembahasan soal:
Demikian penjelasan tentang materi vektor untuk fisika kelas 10 semoga
bermanfaat, jika ada yang perlu didiskusikan bisa tinggalkan komentar di
bawah.bagi yang merasa kesulitan dalam mehamami materi fisika bisa baca tutorial belajar fisika agar semakin paham setelah itu silahkan dicoba untuk mengerjakan soal latihan fisika materi vektor
baca juga :
Sumber :
Homer, D., Jones, M. B. 2014 edition Phycics course companion.
Oxford University press. 2014
Resnick, R., Halliday, D., Walker, J. Fundamentals of Physics, 10th ed., John Wiley & Sons, Inc. 2014
Serway, R. A., Faughn, J. S. Holt Physics. Holt. 2006
Wolfson, R. Essential university physics 2nd ed. Pearson
education, Inc.2012
Young, H. D., Freedman, R. A. Sears ana Zemansky’s university physics : with modern physics 13th ed., Pearson education, Inc.2012










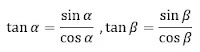




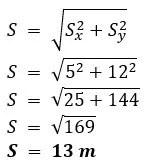
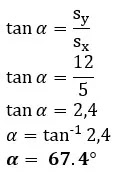




















terima kasih, sangat membantu
BalasHapusSangat membantu sekali,
BalasHapusKomentar ini telah dihapus oleh pengarang.
HapusSyukurlah kalau bermanfaat.. maksih udh baca..
HapusTulsann yang bagus sekali Mas. Sangat membantu saat belajar online. Saya ijin share link agar para siswa mampir ke sini. Terima kasih.
BalasHapusalhamdulillah kalau memang tulisan saya ini bisa membantu masnya, semoga bermanfaat mas
Hapusterima kasih...sangat bagus ulasannya...
BalasHapusSama2, semoga bermanfaat
Hapus