Gerak parabola adalah salah satu materi fisika yang diajarkan di kelas
11 semester 1 tepatnya materi analisis vektor pada gerak dua dimensi. Dikatakan
dua dimensi karna gerak parabola mengalami perubahan posisi baik di sumbu x
dan sumbu y sehingga besaran vektor pada gerak ini juga dianalisis dalam
dua dimensi (lihat kembali materi kelas 10 tentang vektor). Selain pada bidang datar gerak parabola juga sering digambarkan pada bidang miring, tapi sebelumnya mari kita pelajari dulu untuk bidang datar. Gerak parabola pada bidang datar dapat digambarkan sebagai
berikut.
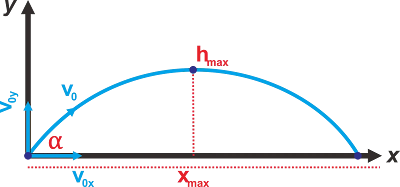
Gambar 1. Gerak parabola pada bidang datar
Sumbu x
gerak benda pada sumbu x adalah gerak lurus beraturan (GLB) sehingga
persamaan matematis yang berlaku hanya
x = vx . t
nilai vx = v0x karena kecepatan benda terhadap sumbu x
tidak berubah (konstan), yang didapatkan dari hasil proyeksi kecepatan
benda terhadap sumbu x yakni
vx = v0x = v0 cos α
Sumbu y
Gerak benda pada sumbu y adalah gerak lurus berubah beraturan (GLBB)
karena pada sumbu y terdapat percepatan gravitasi bumi yang mempengaruhi
kecepatan benda tersebut. Ketika benda bergerak naik dari titik awal ke titik
tertinggi (hmax) benda mengalami GLBB diperlambat dan ketika benda
bergerak turun dari titik tertinggi (hmax) benda mengalami GLBB
dipercepat. Sehingga berlaku persamaan matematis sebagai berikut:
h = v0y t ± ½ gt2
vy = v0y ± gt
vy2 = v0y2 ± 2gh
Gerak parabola pada bidang miring
Gerak parabola suatu benda tidak hanya terjadi
pada bidang datar seperti pembahasan di atas, akan tetapi juga bisa terjadi
pada bidang miring, seperti gambar berikut:
Ganbar 2. Gerak
parabola pada bidang miring
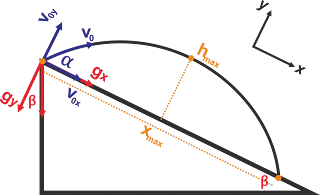
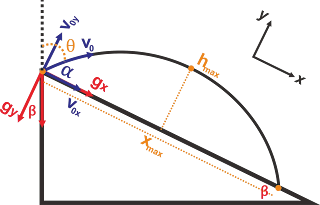
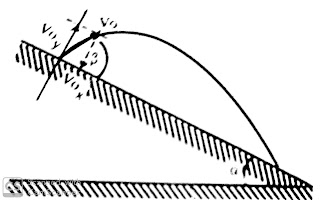
Gambar 3. Diagram
gerak parabola pada bidang miring
Gambar 3, menunjukkan diagram gerak parabola pada bidang miring, dari
gambar tersebut kita dapat mengetahui beberapa perbedaan dengan gerak parabola
di bidang datar yakni diagram kartesian (sumbu x dan sumbu y) mengikuti bidang benda
bergerak (miring – perhatikan gambar pojok kanan atas, percepatan gravitasi (g)
tidak berhimpit dengan sumbu y (membentuk sudut β)
sehingga gerak pada sumbu x tidak lagi GLB melainkan GLBB dipercepat (gx
searah dengan v0x). Untuk menentukan besaran-besaran pada gerak
parabola seperti di atas, dapat dilakukan dengan
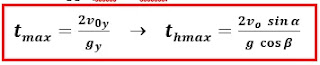
Menentukan besaran waktu
Saat benda bergerak ke atas berlaku
vy = v0y – gy t (dititik tertinggi vy
= 0)
gy t = v0y
gy t = v0ySedangkan waktu total benda selama di udara merupakan dua kali waktu benda mencapai titik tertinggi (tmax = 2 thmax)
Menentukan titik tertinggi (hmax)
hmax = v0y t – ½ gy t2
hmax = v0y (v0y/gy) – ½ gy
(v0y/gy)2
hmax = v0y2/gy
– ½ v0y2/gy
Menentukan jarak terjauh (xmax)
Berbeda dengan gerak parabola pada bidan datar, dimana gerak pada sumbu x
merupakan gerak lurus beraturan. Pada gerak parabola di bidang miring, gerak
pada sumbu x merupakan gerak lurus berubah beraturan (GLBB) karena
dipengaruhi oleh percepatan gravitas (gv). Ketika benda bergerak
turun seperti di atas, benda akan mengalami percepatan akan tetapi ketika benda
bergerak naik benda akan mengalami perlambatan, berikut analisisnya
Gerak parabola menuruni bidang miring
Gerak parabola menaiki bidang miring
Sudut elevasi (α)
agar jangkauannya maksimum
Sudut
elevasi atau sudut tembak gerak parabola pada bidang miring dengan sudut
kemiringan β dapat ditentukan sebagai berikut.
Gerak parabola menuruni bidang
Kita misalkan sudut yang
terbentuk antara kecepatan awal (v0) dengan garis vertikal adalah
sudut θ,
maka berlaku persamaan terlihat seperti gambar berikut!
Berdasarkan
gambar di atas, maka
α + θ – β = 900
atau α – β = 900 – θ ... (1) Berdasarkan persamaan
untuk jarak terjauh (xmax) di atasJangkauan terjauh benda didapatkan ketika nilai sin α cos (α – β) bernilai maksimum. Berdasarkan persamaan (1) di atas dapat kita tuliskan
sin
α
cos (α – β)
= sin α
cos (900 – θ)
sin
α
cos (α – β)
= sin α sin
θ
sin
α
cos (α – β)
= ½ ( 2 sin α sin θ )
sin
α
cos (α – β)
= ½ [ cos (α – θ) - cos (α + θ)]
nilai
(α +
θ)
adalah konstan, sehingga sin α cos (α – β) akan
bernilai maksimum jika cos (α – θ) sama dengan 1
cos
(α –
θ)
= 1
cos
(α –
θ)
= cos 00
α –
θ
= 0
α =
θ
substitusikan
ke persamaan (1)
α – β = 900 –
θ
α – β = 900 –
α
2α = 900 + β
Gerak parabola menaiki bidang
Kita
misalkan sudut yang terbentuk antara kecepatan awal (v0) dengan
garis vertikal adalah sudut θ, dengan cara yang sama seperti sebelumnya, maka berlaku
persamaan
α + β + θ = 900
atau α + β = 900 – θ ... (2) Berdasarkan persamaan
untuk jarak terjauh (xmax) di atas Jangkauan terjauh benda didapatkan ketika nilai sin α cos (α + β) bernilai maksimum. Berdasarkan persamaan (2) di atas dapat kita tuliskan
sin
α
cos (α +
β)
= sin α
cos (900 – θ)
sin
α
cos (α +
β)
= sin α sin
θ
sin
α
cos (α +
β)
= ½ ( 2 sin α sin θ )
sin
α
cos (α +
β)
= ½ [ cos (α – θ) - cos (α + θ)]
nilai
(α +
θ)
adalah konstan, sehingga sin α cos (α +
β) akan
bernilai maksimum jika cos (α – θ) sama dengan 1
cos
(α –
θ)
= 1
cos
(α –
θ)
= cos 00
α –
θ
= 0
α =
θ
substitusikan
ke persamaan (2)
α
+ β = 900 – θ
α
+ β = 900 – α
2α = 900 – β
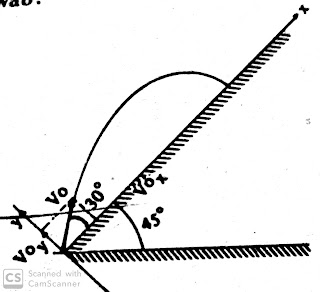
Contoh soal 1
Dari
titik A pada kaki bidang miring yang sudut kemiringannya 450
ditembakkan sebuah peluru dengan kecepatan awal 30√3 m/s yang arahnya membentuk sudut 300
dengan bidang miring. hitunglah
a.
koordinat titik tertinggi yang dicapai peluru dihitung dari kaki bidang miring!
b.
dimana benda jatuh di kaki bidang miring?
pembahasan :
ilustrasi soala.
menentukan waktu yang diperlukan untuk mencapai ketinggian maksimum
Ketinggian maksimum yang dicapai benda
jarak mendatar yang dicapai dalam waktu tersebut
b. benda jatuh di kaki bidang miring menunjukkan jarak terjauh yang mampu dicapai benda tersebut sehingga
baca juga :
materi fisika tingkat SMA
latihan soal fisika tingkat SMA
soal UN Fisika SMA tahun 2018 dan pembahasannya
soal UN Fisika SMA tahun 2019 dan pembahasannya
materi fisika tingkat SMA
latihan soal fisika tingkat SMA
soal UN Fisika SMA tahun 2018 dan pembahasannya
soal UN Fisika SMA tahun 2019 dan pembahasannya
Contoh
soal 2
Sebuah
peluru ditembakkan dari puncak bidang miring dengan kecepatan 200 m/s. hitung
jangkauan maksimum yang mampu dicapai peluru jika sudut kemiringan bidang
adalah 30o.
Ilustrasi soal tersebut
adalahJangkauan maksimum dapat dicapai dengan sudut elevasi:
sehingga
jadi jangkauan terjauh yang mampu ditempuh peluru adalah 8000 m
demikian penjelasan tentang gerak parabola pada bidang miring semoga dapat memberikan pemahaman bagi para pembaca untuk lebih memahami tentang gerak parabola silahkan dibuka juga, materi gerak parabola, latihan soal dan pembahasan gerak parabola, dan praktikum virtual gerak parabola, jangan lupa like, share, dan follow ya...jika ada yang ditanyakan silahkan tinggalkan komentarnya gan...












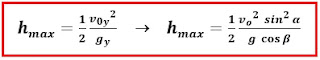
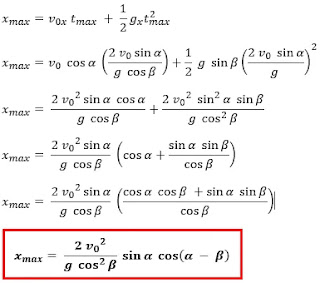
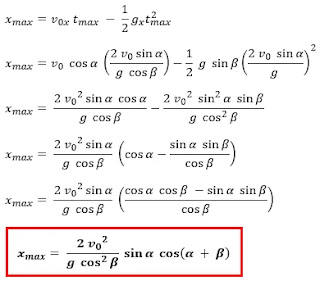














Tidak ada komentar:
Posting Komentar