Gambar 1. Hasil pemeriksaan menggunakan Magnetic Resonance Imagine (MRI)
(sumber : Physics University)
Gambar di atas merupakan salah satu dari aplikasi materi medan magnet yang dipelajari pada mata pelajaran fisika kelas 12, yakni Magnetic Resonance Imagine (MRI) adalah sebuah alat kedokteran yang digunakan untuk memeriksa keadaan di dalam organ tubuh manusia secara lebih akurat daripada menggunakan sinar X seperti yang ditunjukkan pada gambar di atas. prinsip kerja MRI adalah dengan menggunakan konsep medan magnet. Medan magnet selain diaplikasikan dalam bidang kedokteran juga banyak diaplikasikan dalam bidang bangunan, alat-alat berat, dll. oleh karena itu materi ini sangat bermanfaat dalam kehidupan sehari-hari. Silahkan menikmati sedikit ulasan dari saya ini tentang Medan magnet... 😊
Medan Magnet
Pada kelas IX telah dijelaskan bahwa medan magnet merupakan daerah di sekitar magnet yang masih dipengaruhi oleh gaya magnet, sehingga dapat dikatakan bahwa gaya magnet dapat terjadi pada medan magnet yang berinteraksi dengan partikel bermuatan ketika bergerak atau benda magnetik (magnet). Hubungan antara medan magnet dan gaya magnet mirip dengan hubungan antara medan listrik dan gaya listrik dimana gaya listrik juga dapat terjadi apabila ada interaksi antara medan magnet dengan sebuah muatan. Akan tetapi perlu diperhatikan bahwa jika medan listrik ada di sekitar sebuah muatan (bisa muatan positif atau negatif) untuk medan magnet tidak berasal dari muatan magnet (magnet dengan satu kutub), meskipun hal tersebut bisa diprediksikan secara teori, akan tetapi dalam kehidupan sehari-hari tidak ada magnet yang hanya memiliki satu kutub saja.
Medan magnet dapat terjadi pada dua cara yakni medan magnet di sekitar sebuah magnet permanen (seperti kompas, magnet batang, dll) dan medan magnet di sekitar kawat berarus (kawat lurus, melingkar, dan membentuk lilitan). Medan magnet yang timbul di sekitar kawat berarus disebut dengan induksi magnetik (atau medan magnet). Induksi magnetik dilambangkan dengan B yang merupakan besaran vektor sehingga memiliki nilai dan arah.
Medan Magnet Di Sekitar Kawat Berarus
Pada tahun 1820 seorang fisikawan bernama Hans Christian Oersted dalam percobaannya yakni dengan menempatkan beberapa buah kompas di sekitar kawat berarus listrik seperti terlihat di gambar berikut.
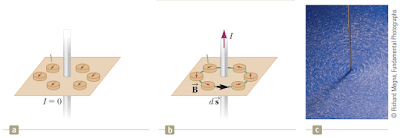
Gambar 2. Percobaan hans christian oersted (a) arah jarum kompas sebelum kawat di aliri arus (b) arah jarum jam menyimpang ketika kawat di aliri arus (c) serbuk besi yang disebarkan di sekitar kawat berarus
(sumber: principle of physics)
Hans Christian Oersted kemudian berdasarkan percobaan yang dilakukan menyatakan bahwa “jika sebuah magnet jarum (kompas) didekatkan pada suatu penghantar yang berarus listrik, magnet jarum akan menyimpang” yang dapat terlihat pada gambar 2b. Adanya pengaruh kuat arus listrik terhadap jarum kompas menunjukkan ketika kawat dialiri arus listrik maka akan timbul suatu medan magnet di sekitar kawat tersebut. Jean-Baptiste Biot (1774 – 1862) dan Félix Savart (1791 – 1841) melakukan eksperimen untuk menentukan besar gaya pada arus listrik di sekitar medan magnet. Berdasarkan hasil eksperimennya Biot-Savart dapat menemukan persamaan matematis untuk menentukan besar induksi magnetik pada sebuah titik di sekitar kawat berarus listrik. Perhatikan gambar berikut
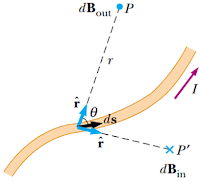
Gambar 3. Induksi magnetik dB pada sebuah titik karena arus I yang melalui elemen panjang ds. arah induksi magnetik keluar bidang pada P dan masuk bidang pada P’
(sumber: physics for scientists and engineers)
Gambar 3 di atas menunjukkan adanya induksi magnet dB yang disebabkan elemen kawat berarus sepanjang ds (P dan P’). Hasil eksperimen yang dilakukan oleh biot-savart menunjukkan beberapa hal yakni:
- Vektor dB tegak lurus dengan ds dan vektor unit ȓ merupakan arah dari ds ke titik P
- Besar vektor dB berbanding terbalik dengan r2, dimana r adalah jarak dari ds ke titik P
- Besar vektor dB sebanding dengan kuat arus dan besar ds
- Besar vektor dB sebanding dengan θ, dimana θ merupakan sudut antara vektor ds dengan ȓ
Sehingga secara matematis dapat ditulis
Persamaan di atas dikenal sebagai hukum biot-savart, dimana μ0 merupakan permeabilitas vakum (μ0 = 4π x 10-7Wb A-1m-1)
Perhatikan persamaan (1) di atas medan dB merupakan induksi magnetik yang disebabkan oleh elemen panjang ds dari sebuah konduktor, sehingga untuk menentukan induksi magnetik total B pada sebuah titik dari kawat berarus maka kita harus menjumlahkan semua elemen arus I ds (kuat arus total) dengan menggunakan metode integrasi. Maka persamaan (1) di atas dapat ditulis
Persamaan (2) menunjukkan adanya perkalian cross antara ds dan ȓ menunjukkan bahwa hasil perkaliannya merupakan besaran vektor (induksi magnetik B). Besarnya induksi magnetik B dapat ditentukan dengan besar perkalian cross adalah |ds x ȓ |= ds sin θ, sehingga persamaan (2) dapat ditulis
Medan magnet di sekitar kawat lurus berarus
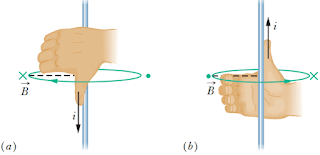
Sebuah kawat lurus sangat panjang yang di aliri oleh arus listrik akan menimbulkan medan magnet di sekitar kawat tersebut. Arah medan magnetnya dapat ditentukan dengan menggunakan kaidah tangan kanan seperti gambar berikut.
Gambar 4. Kaidah tangan kanan untuk menentukan arah medan magnet di sekitar kawat lurus berarus
(sumber: Fundamentals of Physics)
Gambar 4 menunjukkan kaidah tangan kanan untuk menentukan arah medan magnet di sekitar kawat lurus berarus listrik dengan ketentuan:
• Ibu jari menunjukkan arah arus listrik
• Empat jari menunjukkan arah medan magnet
Arah medan magnet di sekitar kawat lurus ditunjukkan oleh empat jari, lebih jauh untuk menggambarkan arah medan magnet dapat digunakan simbol “cross” (⦻) jika arah medan magnet menjauhi pengamat (masuk bidang) dan “dot” (⦿) jika arah medan magnet mendekati pengamat (keluar bidang). Perhatikan kembali gambar 4a, dimana arah arus yang mengalir adalah ke bawah sehingga arah medan magnet di sebelah kiri kawat akan berarah masuk bidang yang ditunjukkan dengan tanda cross (⦻) dan arah medan magnet di sebelah kanan kawat akan berarah keluar bidang yang ditandai dengan tanda dot (⦿). Gambar 4b kebalikan dari gambar 4a dimana arah arus pada kawat adalah ke atas, sehingga arah medan magnet di sebelah kiri kawat berarah keluar bidang yang ditunjukkan dengan tanda dot (⦿), sedangkan arah medan magnet di sebelah kanan kawat berarah masuk bidang yang ditunjukkan dengan tanda cross (⦻).
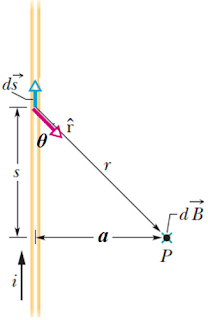
Gambar 5. Menentukan medan magnet yang disebabkan oleh kawat lurus sangat panjang. Elemen medan magnet dB di titik P disebabkan karena arus pada elemen panjang I ds dengan arah masuk bidang
(sumber: fundamentals of physics)
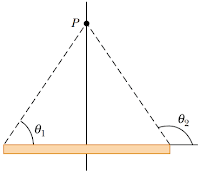
Menentukan total medan magnet di titik P maka kita harus menjumlahkan semua elemen medan magnet yang disebabkan oleh arus listrik pada semua elemen panjang kawat. Untuk itu kita dapat menggunakan konsep integral seperti yang ditunjukkan oleh persamaan (3) dengan batas θ1 sampai θ2 (kawat lurus sangat panjang) sehingga kita dapat menulis persamaan 3 sebagai berikut
Untuk dapat mengintegrasi persamaan di atas, maka kita harus dapat menemukan hubungan antara variabel θ, s dan r, Berdasarkan sifat fungsi sinus, kita dapat menuliskan
Dimana
Sin θ = a/r
r = a/sin θ
r = a csc θ
r2 = a2 csc2 θ ... (a)
tan θ = a/s
s = a/tan θ
s = a cot θ
ds = - a csc2 dθ ... (b)
substitusikan persamaan (a) dan (b) ke persamaan (1) sehingga menjadi
Untuk kawat lurus sangat panjang (dari 0 sampai ∞) maka kita dapat memasukkan nilai θ1 = π dan θ2 = 0, sehingga persamaan (2) dapat ditulis
Perhatikan kembali persamaan (2), persamaan tersebut dapat digunakan ketika kawat lurus yang dialiri arus listrik memiliki panjang tertentu seperti ditunjukkan oleh gambar berikut
Gambar 6. Medan magnet di titik P karena kawat lurus berarus dengan panjang tertentu
(sumber: physics for scientists and engineers)
Sehingga besar medan magnet di titik P ketika kawat lurus berarus dengan panjang tertentu adalah
Medan magnet di sekitar kawat melingkar
Selain disebabkan oleh kawat lurus berarus, medan magnet juga dapat timbul di sekitar kawat melingkar berarus, perhatikan gambar berikut
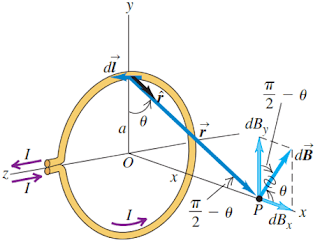
Gambar 7. Elemen kawat melingkar berarus yang menimbulkan medan magnet sebesar dB di titik P
(sumber: Physics university)
Titik P yang berjarak x dari kawat melingkar akan timbul medan magnet yang disebabkan oleh kawat melingkar, untuk menentukan besar medan magnet di titik P kita dapat menggunakan hukum Biot – Savart dan menganalisis seperti sebelumnya yakni dengan meninjau besar elemen medan magnet dB yang disebabkan oleh besar kuat arus yang mengalir pada elemen panjang I dl. Perhatikan kembali gambar 7 di atas, vektor dl dan vektor satuan ȓ saling tegak lurus dan arah medan magnet dB yang disebabkan oleh kuat arus pada elemen dl digambarkan pada bidang x – y. Perhatikan juga bahwa
sehingga besarnya dB yang disebabkan karena kuat arus yang mengalir melalui
dl adalah
Total medan magnet B pada titik P hanya ditentukan dari komponen dBx yang tegak lurus dengan bidang kawat melingkar. Perhatikan kembali gambar 7 di atas, komponen dBy memiliki arah yang sejajar dengan arah bidang kawat (tegak lurus terhadap sumbu x) jika semua komponen dBy digambarkan maka akan menghasilkan arah komponennya saling berlawanan dan sama besar (membentuk sebuah pola lingkaran dengan arah komponen dBy menuju keluar). Oleh karena itu medan magnet total B di titik P hanya ditentukan dari komponen sumbu x. Besar medan magnet B dapat ditentukan dengan melakukan integrasi pada komponen sumbu x sebagai berikut
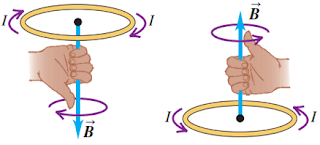
Arah dari medan magnet pada kawat melingkar berarus dapat ditentukan dengan menggunakan kaidah tangan kanan seperti yang terlihat pada gambar berikut ini
Gambar 8. Kaidah tangan kanan untuk menentukan arah medan magnet pada kawat melingkar
(sumber: physics university)
Besar medan magnet yang ditimbulkan oleh kawat melingkar akan semakin besar jika jumlah kawat melingkar diperbanyak (N) dan jarak ke bidang kawat melingkar semakin dekat (x). Ketika jumlah kawat melingkar diperbanyak (disebut juga kumparan) maka persamaan di atas dapat ditulis
N : jumlah kumparan
jumlah kumparan ini menunjukkan kawat berupa kumparan bukan terdiri dari satu kawat. Selain itu semakin dekat ke pusat lingkaran sehingga medan magnet terbesar didapatkan di titik pusat lingkaran (x = 0). Sehingga persamaannya dapat ditulis
Berdasarkan penjelasan di atas, maka kita dapat mengetahui medan magnet terbesar dari kawat melingkar adalah ketika menentukan besar medan magnet di pusat sebuah kawat melingkar dengan N buah lilitan dapat ditentukan dengan persamaan.
Apabila kawat membentuk busur lingkaran (hanya sebagian lingkaran) maka besar medan magnet di pusatnya sebanding dengan bagian busur lingkaran tersebut.
Hukum Ampere
Hukum Ampere dikembangkan oleh André-Marie Ampère (1775–1836) dan disempurnakan oleh fisikawan inggris yakni James Clerk Maxwell. Hukum Ampere ini mirip dengan hukum Gauss yang digunakan untuk menentukan besar medan listrik pada distribusi muatan. Jika hukum Gauss dipengaruhi oleh fluks listrik yang menembus permukaan bidang dimana fluks dipengaruhi oleh total muatan pada permukaan. Berbeda dengan hukum Gauss, pada hukum Ampere besar medan magnet tidak dipengaruhi oleh distribusi arus listrik.
Hukum Ampere dapat ditentukan dengan integral garis terhadap medan magnet B yang dibatasi oleh suatu daerah yang dibatasi oleh suatu lintasan atau garis tertutup (closed path). Secara matematis dapat ditulis
Untuk menyelesaikan persamaan di atas, maka kita dapat menghitung perkalian skalar antara B ∙ dl kemudian menjumlahkannya. Nilai medan magnet B bisa berbeda-beda pada setiap elemen dl yang merupakan bagian dari panjang garis pada daerah tersebut. perhatikan gambar berikut
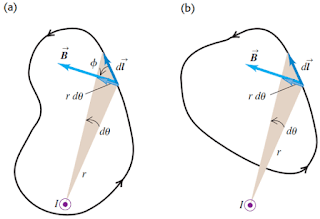
Gambar 9. (a) medan magnet B sepanjang lintasan tertutup yang disebabkan oleh kawat berarus I dengan arah keluar bidang (kawat berada di dalam lintasan tertutup). (b) medan magnet B sepanjang lintasan tertutup yang disebabkan oleh kawan berarus I dengan arah keluar bidang (kawat berada di luar lintasan tertutup)
(sumber: physics university)
Kita dapat menentukan besar medan magnet B seperti pada gambar 9a di atas dengan menggunakan hukum ampere dimana nilai perkalian titik antara medan magnet dengan elemen panjang adalah
B . dl = B dl cos ϕ
Berdasarkan gambar 9a. dl cos ϕ = r dθ , dimana dθ adalah sudut yang terbentuk antara elemen panjang dl pada titik sepanjang lintasan dengan r (jarak antara dl dengan kawat konduktor) sehingga persamaan di atas dapat kita tulis
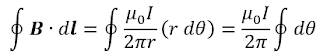
Perhatikan kembali gambar 9a, maka sebenarnya nilai dari ∮ dθ = θ dimana θ total sudut yang dibentuk jika jari-jari diputar sesuai dengan lintasan tertutup sehingga nilai θ = 2π (3600). Maka kita akan mendapatkan persamaan hukum Ampere sebagai berikut

Persamaan tersebut tidak bergantung pada bentuk bidang yang terbentuk oleh lintasan tertutup dan arah dari medan magnet dapat ditentukan dengan menggunakan aturan kaidah tangan kanan. Berbeda dengan sebelumnya pada gambar 9b terlihat bahwa kawat tidak berada di dalam daerah lintasan tertutup sehingga ∮ dθ = 0 maka hasil integrasinya juga akan sama dengan nol atau ∮ B dl = 0. Hasil ini tidak berarti bahwa medan magnet di sepanjang lintasan sama dengan nol, akan tetapi nilai total medan magnetnya sama dengan nol.
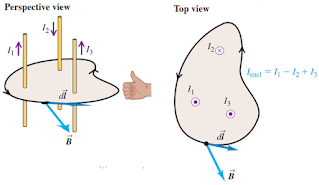
Penerapan hukum ampere ini tidak hanya sebatas untuk satu kawat lurus saja akan tetapi juga bisa diterapkan untuk beberapa kawat lurus sangat panjang yang terletak paralel pada daerah yang dibatasi oleh lintasan tertutup, perhatikan gambar berikut
Gambar 10. Medan magnet karena beberapa kawat lurus sangat panjang yang dipasang paralel
(sumber: physics university)
Perhatikan gambar 10 di atas, terlihat pada daerah yang di arsir terdapat tiga buah kawat lurus berarus sangat panjang yang dipasang paralel, ketiga kawat tersebut tentunya akan memberikan pengaruh medan magnet pada tiap elemen panjang dl di sepanjang lintasan. Arah arus penting untuk diperhatikan karena arah arus akan mempengaruhi arah medan magnet yang ditimbulkannya, jika arah arusnya berlawanan tentu arah medan magnet yang ditimbulkan juga akan berlawanan. Kita dapat menentukan medan magnet total pada daerah tersebut dengan sedikit memodifikasi persamaan pada hukum Ampere seperti berikut ini.
Ruas kanan pada persamaan tersebut menunjukkan kuat arus total dari ketiga kawat tersebut untuk menentukan kuat arus total ini perhatikan arah arusnya jika arus searah maka dijumlahkan dan jika arah arus berlawanan maka dikurangi (perhatikan gambar 10 top view)
Medan magnet di solenoida
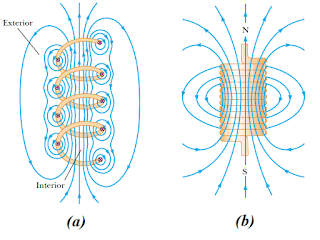
Solenoida dapat digambarkan sebagai sebuah kawat yang digulung melingkar membentuk helix seperti yang ditunjukkan oleh gambar 11a
Gambar 11. (a) medan magnet pada solenoida (b) garis – garis medan magnet dan kutub magnet pada solenoida
(sumber: physics for scientists and engineers)
Ketika kawat dialiri oleh arus listrik maka medan magnet akan timbul di antara ruang antara lilitan kawat yang disebut dengan medan magnet interior . Selain itu solenoida juga dapat diasumsikan sebagai kumpulan kawat melingkar (loop) yang dihubungkan menjadi satu sehingga medan magnet total dapat ditentukan dengan menjumlahkan medan magnet yang terbentuk pada seluruh loop.
Perhatikan kembali gambar 11a di atas, garis-garis gaya magnet pada bagian tengah solenoid (interior) hampir sejajar, terdistribusi merata dan berdekatan yang menunjukkan bahwa medan magnet pada area ini kuat dan merata besarnya. Pada bagian antar loop satu dengan loop yang lain, terdapat medan magnet pada masing-masing kawat. Medan magnet pada bagian ini secara keseluruhan dapat dilihat pada gambar 11b, berdasarkan hal tersebut maka dapat diketahui salah satu ujung solenoida bertindak sebagai kutub utara dan ujung lainnya bertindak sebagai kutub selatan, selain itu jika diperhatikan lebih jauh jarak antara garis medan magnet pada bagian luar (exterior) lebih renggang dari pada jarak garis medan magnet pada bagian dalam hal ini menunjukkan medan magnet di bagian dalam lebih kuat daripada medan magnet di bagian luar. Jika solenoida semakin panjang maka medan magnet bagian dalam akan lebih merata (semakin sejajar) sedangkan medan magnet di bagian luar semakin lemah (garis medan magnetnya semakin longgar). Solenoida akan semakin ideal jika jarak antara loop semakin rapat dan panjang solenoida lebih besar dari jari-jari loop.
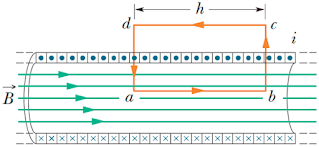
Gambar 12. Penampang solenoida ideal yang dialiri arus sebesar i. Aplikasi hukum ampere pada abcd untuk menentukan besar medan magnet pada solenoida
(sumber: fundamentals of physics)
Gambar 12 menunjukkan penampang sebuah solenoida ideal jika dilihat dari atas yang dialiri arus sebesar i yang digambarkan dengan simbol ⦿ (masuk bidang) dan simbol ⦻ (keluar bidang). Untuk solenoida ideal kita dapat mengasumsikan bahwa kuat medan magnet di luar solenoida sangat kecil (mendekati nol) sedangkan kuat medan magnet di dalam solenoida tersebar merata dan sejajar. Besar medan magnet pada solenoida dapat ditentukan dengan menjumlahkan hasil integrasi ∮ B . dl pada masing-masing bagian dari loop abcd seperti berikut ini
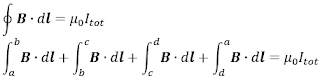
Hasil integrasi pada bagian bc dan da sama dengan nol hal ini dikarenakan setiap elemen dl tegak lurus dengan medan magnet B sehingga hasil perkalian dot product B . dl = 0, sedangkan hasil integrasi pada bagian cd juga sama dengan nol hal ini dikarenakan bagian cd berada di luar soleoinda (perhatikan kembali asumsi awal, bahwa medan magnet di luar solenoida mendekati nol). Sehingga medan magnet pada solenoida hanya bergantung pada medan magnet di dalam solenoida (pada bagian ab), maka persamaan di atas dapat ditulis
BL+0+0+0=μ0 Itot
BL=μ0 Itot
Dimana L adalah panjang solenoida.
Jika dalam solenoida sepanjang L terdapat N buah lilitan (loop) maka kuat arus total pada rentang tersebut adalah Itot = NI , sehingga persamaan di atas dapat ditulis
BL=μ0 NI
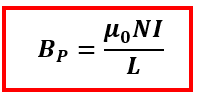
Persamaan di atas adalah persamaan yang digunakan untuk menentukan besar medan magnet di pusat solenoida (Bp). Perlu diketahui bahwa medan magnet terbesar solenoida berada pada titik pusatnya, semakin mendekati ujung maka medan magnetnya semakin kecil, untuk panjang solenoida yang jauh lebih besar dibandingkan dengan jari-jarinya maka medan magnet di ujung solenoida sama dengan setengah dari medan magnet di pusat solenoida. Secara matematis dapat ditulis
Medan magnet di toroida
Toroida mirip seperti solenoida yang berbentuk melingkar, seperti ditunjukkan gambar berikut
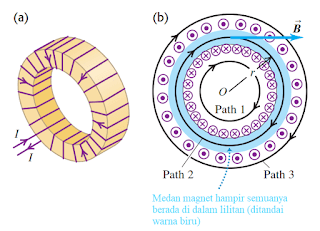
Gambar 13. (a) sebuah toroida ketika kawat melingkar di aliri arus sebesar I (b) gambar penampang medan magner yang berada disekitar lilitan toroida (ditandai dengan simbol ‘dot’ dan ‘cross’
(sumber: physics university)
Ketika suatu toroida di aliri arus listrik, maka arus listrik akan bergerak sesuai dengan kawat (gambar 13a) tiap melewati loop maka akan terbentuk medan magnet di sekitar kawat, karena kawat berada pada posisi melingkar maka akan terbentuk 3 medan magnet seperti yang ditunjukkan pada gambar 13b. Berdasarkan penjelasan pada bagian solenoida di atas yang menyatakan bahwa medan magnet di luar lilitan besarnya sangat kecil (mendekati nol) jika dibandingkan dengan medan magnet di dalam lilitan. Oleh karena itu besar medan magnet di bagian 1 (path 1) dan di bagian 3 (path 3) sama dengan nol, sehingga dapat dikatakan untuk menentukan besar medan magnet pada toroida dapat dilakukan dengan cara menentukan besar medan magnet di dalam kumparan atau pada bagian 2 (path 2).
Medan magnet pada bagian 2 dapat ditentukan dengan melakukan integrasi pada hukum ampere sebagai berikut
∮B . dl = μ0 Itot
B ∮ dl = μ0 Itot
Perhatikan bahwa Itot merupakan total arus yang menimbulkan medan magnet pada toroida, jika untuk satu loop kuat arus yang mengalir sebesar I, maka untuk N buah loop kuat arus total yang mengalir adalah NI, selain itu hasil ∮ dl merupakan keliling dari lingkaran (toroida berbentuk lingkaran) yakni sebesar 2πr. Jadi persamaan di atas dapat ditulis
B 2πr = μ0 NI
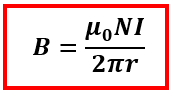
demikian penjelasan singkat terkait dengan materi medan magnet untuk fisika kelas 12, jika ada yang perlu ditanyakan bisa menuliskannya di kolom komentar, semoga bermanfaat. Agar lebih memahmi materi medan magnet silahkan diliat
Latihan soal dan pembahasan Medan magnet untuk kelasa 12










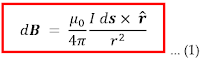
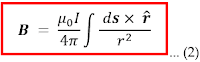
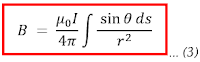

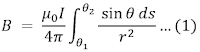
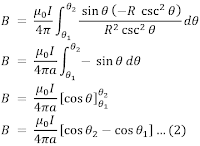
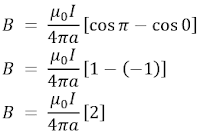
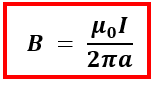

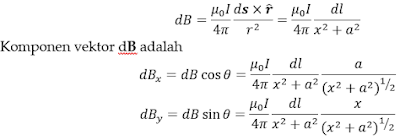

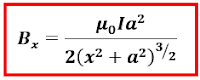
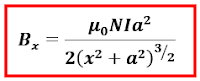
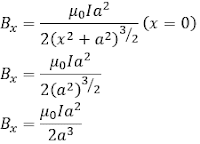
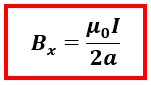
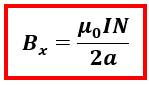
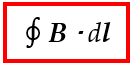

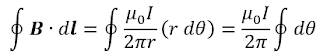

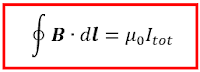


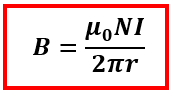




Tidak ada komentar:
Posting Komentar