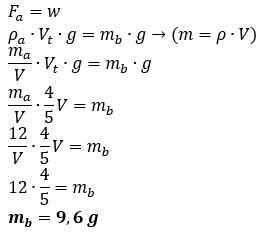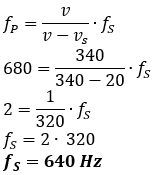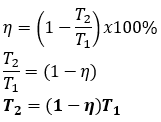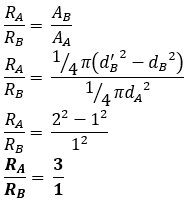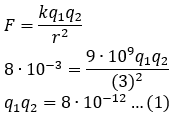-

Materi Fisika Lengkap dan Mudah Dipahamie
Pelajari konsep dasar hingga lanjutan fisika dengan penjelasan yang sederhana, sistematis, dan dilengkapi contoh nyata dalam kehidupan sehari-hari.
-

Latihan soal dan pembahasan lengkap
Tingkatkan pemahamanmu melalui berbagai latihan soal fisika yang disertai pembahasan langkah demi langkah.
-

Persiapan Ujian masuk sekolah dan perguruan tinggi
Kuasai soal-soal ujian masuk favorit beserta pembahasan lengkap untuk membantu meraih hasil terbaik.
-

Artikel fisika seru dan inspiratif
Temukan sisi menarik dari fisika melalui artikel ringan yang menghubungkan teori dengan fenomena alam di sekitar kita.
-

Belajar fisika jadi menyenangkan
Nikmati pengalaman belajar fisika yang interaktif, mudah dipahami, dan bermanfaat untuk prestasi akademikmu.
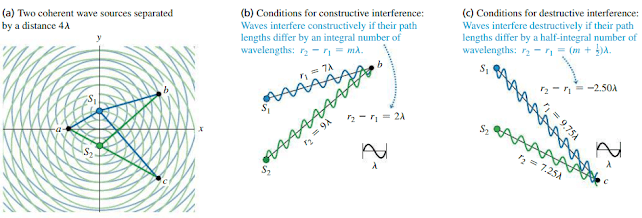
Interferensi Cahaya pada Celah Ganda Young (Materi fisika kelas 11)
Galeri pelajaran versi desain kaos (2)
Iseng-iseng buat desain yang terinspirasi dari konsep-konsep materi pelajaran, seperti konsep fisika, kimia, biologi, dll. Siapa tau para pembaca ada yg berminat, krn belajar tidak harus dari buku hehehe, berikut beberapa desainnya
Mau punya kaos seperti ini ? Cek disini
shoppe : shoopee.co.id/hqim18
web : http://tee.pub/lic/hakim91
LATIHAN SOAL UTBK 2022 - FISIKA | PAKET 2
Untuk mempersiapkan diri bagi siswa/i kelas 12 yang akan mengikuti UTBK tahun 2022, maka pada kesempatan kali ini saya akan memberikan beberapa latihan soal pada mata pelajaran Fisika. Soal – soal yang ada di bawah ini sudah disertai pembahasannya dan dihimpun dari berbagai sumber. Selamat menikmati
Soal nomor 1
Sebuah balok plastik homogen mengapung di suatu bejana air. Seperlima bagian balok
berada di atas permukaan air. Jika volume balok V dan massa air sebanyak V tersebut
adalah 12 g maka massa balok adalah … g
A. 9,2
B. 9,4
C. 9,6
D. 9,8
E. 10,0
Kunci jawaban: "C"
Soal nomor 2
Sebuah balon yang awalnya berisi gas 1 liter ditambahkan gas yang sama sehingga volume balon menjadi 1,2 liter dan massa gas di dalam balon menjadi satu setengah kalinya. Jika suhu gas tetap maka rasio pertambahan tekanan terhadap tekanan awalnya adalah…
A. 0,25
B. 0,33
C. 0,50
D. 0,67
E. 0,75
Kunci jawaban: "A"
Berdasarkan soal dapat diketahui
V1 = 1 liter
V2 = 1,2 liter
m2 = 1,5 m1
∆P/P1 ...?
Untuk gas ideal berlaku persamaan umum
PV = nRT
PV = (m/Mr) RT
PV/m = RT/Mr (konstan)
Dari persamaan di atas kita dapat menggunakan bagian di ruas kiri sebagai persamaan perbandingannya untuk menentukan P2 yakni
Dengan ∆P = P2 – P1, maka rasio perbandingan pertambahan tekanan terhadap tekanan akhirnya dapat ditentukan sebagai berikut
Soal nomor 3
Sebuah bola pejal bermassa M dengan momen inersia I menggelinding pada bidang miring dari keadaan diam dengan ketinggian h. Cara yang dapat dilakukan untuk memperbesar kelajuan linier bola pejal tersebut menjadi dua kalinya adalah ...
A. Memperbesar M menjadi 2M
B. Memperbesar I menjadi 2I
C. Memperbesar I menjadi 4I
D. Memperkecil I menjadi 0,25I
E. Memperbesar h menjadi 4h
Kunci jawaban: "E"
Bola menggelinding, berarti bola tersebut melakukan dua gerakan yakni gerak rotasi dan gerak translasi, sehingga memiliki dua jenis energi kinetik yaitu energi kinetik rotasi dan energi kinetik translasi. Untuk bola menggelinding di bidang miring berlaku hukum kekekalan energi sebagai berikut.
EP = EKT + EKR
mgh = ½ mv2 + ½ I ω2
mgh = ½ mv2 + ½ (k mr2) (v/r)2
dimana “k” merupakan konstanta inersia, untuk bola pejal k = 2/5
mgh = 1/2 mv2 + 1/2 . 2/5 mv2
gh = 1/2 v2 + 1/5 v2
gh = 7/10 v2
v2 = 10/7 gh
berdasarkan persamaan di atas maka kita dapat mengetahui bahwa kuadrat kecepatan sebanding dengan ketinggian dan percepatan gravitasi, sehingga agar kecepatannya menjadi dua kali semula dapat dilakukan dengan cara
- Memperbesar ketinggian menjadi 4 kali semula
- Memperbesar percepatan gravitasi menjadi 4 kali semula
Soal nomor 4
Bila perbandingan jari-jari sebuah planet (Rp) dan jari-jari bumi (Rb) adalah 2 : 1, sedangkan massa planet (Mp) dan massa bumi (Mb) berbanding 10 : 1, maka orang yang beratnya di bumi 100 N, di planet menjadi ....
A. 100 N
B. 200 N
C. 250 N
D. 400 N
E. 500 N
Kunci jawaban: "C"
Berdasarkan soal dapat diketahui
Rp: Rb = 2 : 1
Mp : Mb = 10 : 1
Fb = 100 N
Fp ... ?
untuk gaya berat (gaya gravitasi) dapat ditentukan dengan persamaan
Berdasarkan persamaan di atas kita dapat mengetahui bahwa gaya berat sebanding dengan massa planet dan berbanding terbalik dengan kuadrat jari-jarinya, sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut
Soal nomor 5
Benda A dan B bermassa sama masing-masing 2 kg saling bertumbukan. Kecepatan sebelum tumbukan adalah vA = 15i + 30j (m/s) dan vB = -10i + 5j (m/s). kecepatan benda A setelah tumbukan adalah -5i + 20j (m/s). persentase energi kinetik yang hilang setelah tumbukan adalah ....
A. 10%
B. 20%
C. 40%
D. 60%
E. 80%
Kunci jawaban: "C"
Berdasarkan soal dapat diketahui
mA = mB = 2 kg
vA = 15i + 30j
vB = -10i + 5j
vA’ = -5i + 20j
persentase energi kinetik setelah tumbukan..?
untuk mengetahui persentase energi kinetik setelah tumbukan, maka kita harus mengetahui kecepatan kedua benda setelah tumbukan dengan menggunakan hukum kekekalan momentum sebagai berikut
mA vA + mB vB = mA vA’ + mB vB’
vA + vB = vA’ + vB’
(15i + 30j) + (-10i + 5j) = (-5i + 20j) + vB’
(15 - 10 + 5)i + (30 + 5 – 20)j = vB’
vB’ = 10i + 15j (m/s)
Menentukan besar kuadrat kecepatan masing-masing benda
vA2 = 152 + 302
vA2 = 225 + 900
vA2 = 1125
vB2 = (-10)2 + 52
vB2 = 100 + 25
vB2 = 125
vA’2 = (-5)2 + 202
vA’2 = 25 + 400
vA’2 = 425
vB’2 = 102 + 152
vB’2 = 100 + 225
vB’2 = 325
Menentukan energi kinetik awal
EK0 = EKA + EKB
EK0 = ½ mA vA2 + ½ mB vB2
EK0 = ½ m (vA2 + vB2)
EK0 = ½ . 2 (1125 + 125)
EK0 = 1250 J
Menentukan energi kinetik akhir
EK’ = EKA’ + EKB’
EK’ = ½ mA vA’2 + ½ mB vB’2
EK’ = ½ m (vA’2 + vB’2)
EK’ = ½ 2 (425 + 325)
EK’ = 750 J
Menentukan jumlah energi kinetik yang hilang
∆EK = EK0 – EK’
∆EK = 1250 – 750
∆EK = 500 J
Persentase kehilangan energi kinetik
η = (∆EK/EK0)*100%
η = (500/1250)*100%
η = 40%
Soal nomor 6
empat buah muatan masing-masing 10μC, 20μC, -30μC, dan 40μC, ditempatkan pada titik sudut sebuah empat persegi panjang dengan sisi 60 cm, 80 cm. potensial listrik pada titik tengah empat persegi panjang tersebut adalah ....
A. 150 kV
B. 360 kV
C. 720 kV
D. 1440 kV
E. 2880 kV
Kunci jawaban: "C"
Soal di atas dapat diilustrasikan sebagai berikut!
Panjang diagonal persegi panjang
d2 = 802 + 602
d = 100 cm (pasangan phytagoras, 60 , 80 , 100)
jarak muatan ke titik tengah (P)
r = ½ d
r = ½ . 100
r = 50 cm
r = 0,5 m
karena potensial listrik merupakan besaran skalar, maka untuk menentukan potensial di titik tengahnya dapat dilakukan dengan menjumlahkannya, tapi perhatikan jenis muatan yang digunakan. Jika muatan positif menghasilkan potensial positif, dan jika muatan negatif menghasilkan potensial negatif. Jadi potensial listrik di titik P adalah
Soal nomor 7
Pipa organa terbuka yang panjangnya 25 cm menghasilkan frekuensi nada dasar sama dengan frekuensi yang dihasilkan oleh dawai yang panjangnya 150 cm. Jika cepat rambat bunyi di udara 340 m/s dan cepat rambat gelombang transversal pada dawai 510 m/s maka dawai menghasilkan:
A. nada dasar
B. nada atas pertama
C. nada atas kedua
D. nada atas ketiga
E. nada atas keempat
Kunci jawaban: "D"
berdasarkan soal dapat diketahui
LP = 25 cm = 0,25 m
LD = 150 cm = 1,5 m
vP = 340 m/s
vD = 510 m/s
nada pada dawai, ketika nada dasar pada pipa organa terbuka ...?
frekuensi nada dasar pipa organa terbuka berlaku persamaan
f = vP/2LP
persamaan umum frekuensi pada dawai
f = (n + 1)vD/2LD ... ( n = 0, 1, 2, 3, ... )
karena frekuensinya sama, maka kedua persamaan di atas dapat ditulis
n = 0 → nada dasar
n = 1 → nada atas pertama
n = 2 → nada atas kedua
n = 3 → nada atas ketiga
Soal nomor 8
Susunan tiga buah hambatan yang besarnya sama menghasilkan hambatan 2 . Jika susunanya diubah, maka dapat dihasilkan hambatan 1 . Besar hambatan tersebut adalah.....
A. 1 Ω
B. 2 Ω
C. 3 Ω
D. 4 Ω
E. 5 Ω
Kunci jawaban: "C"
Tiga hambatan sama besar jika dirangkai paralel hasilnya 1 Ω adalah
Rp = n/R
R = n/Rp
R = 3/1
R = 3 Ω
3 buah hambatan 3 Ω, Untuk menghasilkan hambatan total sebesar 2 Ω maka 2 resitor di rangkai seri kemudian di rangkai paralel dengan resistor yang ketiga.
Rs = 3 + 3 = 6 Ω
1/Rp = 1/6 + 1/3
1/Rp = 1/6 + 2/6
1/Rp = 3/6
Rp = 2 Ω
Soal nomor 9
Sebuah kubus memiliki volume sejati 1000 cm Volume kubus tersebut menurut seorang pengamat yang bergerak dengan kecepatan 0,8 c relatif terhadap kubus dalam arah sejajar salah satu rusuknya adalah...
A. 100 cm3
B. 300 cm3
C. 400 cm3
D. 500 cm3
E. 600 cm3
Kunci jawaban: "E"
Berdasarkan soal dapat diketahui
V0 = 1000 cm
v = 0,8 c
V...?
Ketika kubus di amati oleh pengamat yang bergerak searah dengan salah satu rusuknya, maka terjadi perubahan panjang dari rusuk tersebut (yang searah dengan gerak pengamat). Sesuai dengan persamaan pemekaran panjang yakni
L = L0/γ ,
maka persamaan untuk Volume relativistik adalah
V = V0/γ
Untuk pengamat yang bergerak dengan kecepatan
v = 0,8 c
v = 8/10 c,
maka dengan menggunakan konsep phytagoras kita dapat langsung menentukan nilai γ yakni
γ = 10/6, sehingga
V = 1000 . 6/10
V = 600 cm3
Soal nomor 10
Sebuah tali digetarkan dengan frekuensi 5 Hz menghasilkan gelombang beramplitudo 12 cm dan kelajuan gelombang 20 m/s. Dari pernyataan berikut yang sesuai dengan gelombang yang dihasilkan oleh getaran tali adalah....
1) Frekuensi anguler gelombang 31,4rad/s
2) Panjang gelombang 4 m
3) Persamaan gelombang 0,12 sin 2π (0,25 x - 5 t) m
4) Angka gelombang adalah 1,57 m
A. Jika (1), (2), dan (3) benar
B. Jika (1) dan (3) benar
C. Jika (2) dan (4) benar
D. Jika hanya (4) yang benar
E. Jika semuanya benar
Kunci jawaban: "E"
Berdasarkan soal dapat diketahui
f = 5 Hz
A = 12 cm
v 20 m/s
Tips :
Untuk mengerjakan soal tipe pernyataan, sebenarnya kita tidak harus membuktikan semua pernyataan atau harus dimulai dari pernyataan pertama. Kita bisa memulai dengan membuktikan pernyataan yang paling mudah untuk dibuktikan (bisa dibuktikan benar atau salah) kemudian mencocokkan dengan pilihan jawabannya.
Pernyataan 2
v = f λ
20 = 5 λ
λ = 4 (benar)
perhatikan pilihan A, C, dan E
pernyataan 1
ω = 2π f
ω = 2 . 3,14 . 5
ω = 31,4 rad/s (benar)
perhatikan pilihan A dan E
pernyataan 4
k = 2π/λ
k = 2 . 3,14 / 4
k = 1,57 (benar)
perhatikan pilihan E
Soal nomor 11
Beta berlari menjauhi sebuah mobil yang mengeluarkan suara keras, sehingga kecepatan relatif Beta terhadap mobil adalah nol. Apabila mobil bergerak dengan kecepatan 10 m/s dan frekuensi bunyi yang dikeluarkan mobil 300 Hz, maka frekuensi yang diterima Beta adalah ….
A. 280 Hz
B. 300 Hz
C. 330 Hz
D. 340 Hz
E. 350 Hz
Kunci jawaban: "B"
Perhatikan bahwa kecepatan relatif beta terhadap mobil sama dengan nol, maka dapat dikatakan bahwa beta bergerak dengan besar kecepatan dan arah kecepatannya sama dengan mobil, sehingga kita dapat mengilustrasikan soal di atas seperti berikut
Tips :
Perhatikan ilustrasi di atas, terlihat sumber mendekati pendengar sehingga ia ingin suara terdengar lebih keras dan pada persamaan efek doppler sumber sebagai penyebut (di bawah) sehingga ia harus bernilai minimal (negatif), sedangkan pendengar juga ingin menjauhi sumber sehingga ia ingin suara terdengar lebih pelan dan pada persamaan efek doppler sumber bertindak sebagai pembilang (di atas) sehingga ia harus bernilai minimal (negatif).
Persamaan efek dopplernya dapat dituliskan
Soal nomor 12
Tiga buah kapasitor disusun paralel dalam rangkaian sesuai gambar berikut.
Total muatan tersimpan dalam kapasitor adalah ….
A. 1 C
B. 2 C
C. 3 C
D. 4 C
E. 5 C
Kunci jawaban: "E"
Perhatikan pada ketiga kapasitor di atas, di rangkai paralel sehingga kapasitas kapasitor total pada rangkaian adalah...
Ctot = C1 + C2 + C3
Ctot = 1 + 2 + 2
Ctot = 5 F
Muatan total dalam rangkaian
Q = C . V
Q = 5 . 1
Q = 5 C
Soal nomor 13
li memiliki luas penampang sama dan modulus Young berbeda. Tali pertama memiliki panjang awal 𝑙, sementara tali kedua memiliki panjang awal 2𝑙. Perbandingan modulus Young tali kedua dengan tali pertama adalah 3:1. Bila kedua tali disambung dan digantungi beban bermassa 𝑀, maka pertambahan panjang total tali adalah 0,25𝑙. Pertambahan panjang tali pertama adalah ….
A. 0,05𝑙
B. 0,10𝑙
C. 0,08𝑙
D. 0,15𝑙
E. 0,20𝑙
Kunci jawaban: "D"
Berdasarkan soal kita dapat mengetahui
L1 = 𝑙
L2 = 2 𝑙
E2 : E1 = 3 : 1
∆Ltot = 0,25 𝑙
∆L1 ... ?
Soal di atas dapat diilustrasikan sebagai berikut
Berdasarkan persamaan modulus Young
E = FL/A∆L
Maka kita dapat mengetahui bahwa
Modulus Young sebanding dengan panjang awal
Modulus Young berbanding terbalik dengan pertambahan panjang
Sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut
Dimana
∆L1 + ∆L2 = 0,25l
Maka
∆L1 = (3/5) . 0,25l
∆L1 = 0,15l
Soal nomor 14
Elektron memiliki muatan negatif sebesar 1,6 × 10−19 dan bergerak sepanjang sumbu 𝑥 dengan kecepatan 5 × 105 m/s. Elektron bergerak melewati medan magnet 5 T sesuai gambar berikut.
Besar dan arah gaya Lorentz yang bekerja terhadap elektron adalah ….
A. 4 × 10−14 N ke atas
B. 4 × 10−14 N ke bawah
C. 4 × 10−13 N ke atas
D. 4 × 10−13 N ke bawah
E. 4 × 10−12 N ke atas
Kunci jawaban: "C"
Berdasarkan soal dapat diketahui
Q = 1,6 . 10-19 C
v = 5 . 105
B = 5 T
F (besar dan arah) ...?
Untuk muatan negatif (elektron) Arah gaya Lorentz dapat ditentukan dengan kaidah tangan kiri
- Ibu jari sebagai arah kecepatan
- Telunjuk sebagai arah medan magnet
- Jari tengah sebagai arah gaya lorentz
Besar gaya lorentz dapat ditentukan dengan persamaan
F = B q v
F = 5 x 5 . 105 x 1,6 . 10-19
F = 40 . 10-14
F = 4 . 10-13 N
Soal nomor 15
Sebuah benda bermassa 𝑀 = 10 kg terikat pada tali yang terhubung dengan katrol tak bermassa. Dari katrol hingga ujung, tali memiliki kemiringan 𝜃 = 300. Ujung tali ditarik dengan gaya sebesar 𝐹
Apabila sistem tersebut diam, kita dapat menyimpulkan bahwa ….
A. 𝐹 = 100 N
B. 𝐹𝑥 = 100 N
C. 𝐹𝑦 = 100 N
D. 𝐹𝑦 + 𝑇 = 100 N
E. 𝐹𝑥 + 𝑇 = 100 N
Kunci jawaban: "A"
Karena katrol dalam keadaan diam, maka sistem di atas dapat kita tinjau dalam sistem 1 dimensi, sehingga kita tidak perlu menguraikannya menjadi Fx dan Fy, dalam keadaan diam berlaku persamaan
F = w
F = m . g
F = 10 . 10
F = 100 N
LATIHAN SOAL UTBK 2022 - FISIKA | PAKET 1
Untuk mempersiapkan diri bagi siswa/i kelas 12 yang akan mengikuti UTBK tahun 2022, maka pada kesempatan kali ini saya akan memberikan beberapa latihan soal pada mata pelajaran Fisika. Soal – soal yang ada di bawah ini sudah disertai pembahasannya dan dihimpun dari berbagai sumber. Selamat menikmati
Soal nomor 1
Sebuah bola akan dilemparkan dari sebuah Balon udara yang memiliki ketinggian 20 m dari atas tanah. Bila pesawat bergerak dengan kecepatan konstan arah sumbu x positif sebesar 𝑣 saat menjatuhkan bola dengan percepatan gravitasi 10 𝑚/𝑠2 ,Tentukan jarak antara bola dan balon udara setelah satu detik!
A. 10 m
B. 15 m
C. 20 m
D. 5 m
E. 0
Kunci jawaban: "B"
Berdasarkan soal dapat diketahui:
h = 20 m
g = 10 m/s2
t = 1 s
s ... ?
Karena pada awalnya bola dan balon bergerak bersama-sama dengan kecepatan v ke arah sumbu x positif, maka jarak antara bola dan balon merupakan jarak vertikalnya (sumbu y) yang mana bola melakukan gerak jatuh bebas. Sehingga untuk menyelesaikan soal ini kita dapat menggunakan persamaan
y = y0 - voyt + ½ gt2
y = 20 - 0 + ½ 10 12
y = 20 – 5
y = 15 m
Soal nomor 2
kawat timah dan kawat besi yang masing-masing memiliki panjang 35 cm dan 50 cm juga luas penampang 1 𝑐𝑚2 𝑑𝑎𝑛 1 𝑐𝑚2 disambung dan kemudian digantung beban dengan massa 0,1 ton. Berapakah pertambahan panjang system gabungan kedua kawat tersebut?
(modulus young kawat timah = 3,5 𝑥 1010 𝑁/𝑚2 ,dan modulus young kawat besi = 2,5 𝑥 1010 𝑁/
𝑚2)
A. 0,1 mm
B. 0,2 mm
C. 0,3 mm
D. 0,4 mm
E. 0,5 mm
Kunci jawaban: "C"
Berdasarkan soal dapat diketahui
L1= 35 cm = 35 x 10-2 m
L2 = 50 cm = 50 x 10-2 m
A1 = A2 = 1 cm2 = 10-4 m2
m = 0,1 ton = 100 kg
E1 = 3,5 𝑥 1010 𝑁/𝑚2
E2 = 2,5 𝑥 1010 𝑁/𝑚2
Karena kedua kawat disambung hal itu berarti kedua kawat disambung secara seri. Sehingga konstanta pegas gabungan kedua kawat dapat ditentukan dengan persamaan
Ketika beban digantungkan maka pertambahan panjang kawat dapat ditentukan dengan persamaan
F = k . ∆x
m . g = k . ∆x
100 . 10 = 1/3 . 107 . ∆x
103 = 1/3 . 107 . ∆x
∆x = 3 . 10-4 m
∆x = 0,3 mm
Soal nomor 3
Sebuah kapal laut sedang berdiam di atas lautan. Seorang anak nakal dengan sengaja membuang koper milik ibunya ke dalam air. Apakah yang terjadi terhadap ketinggian laut? Asumsikan massa jenis koper lebih tinggi dari kapal beserta isinya!
A. Ketinggian laut naik karena ada benda yang dicelupkan ke dalam air
B. Ketinggian laut tetap karena koper awalnya juga berada di dalam kapal
C. Ketinggian laut turun sesaat saat koper dilempar oleh sang anak dan kembali ke posisi awal saat koper tenggelam seluruhnya
D. Ketinggian laut turun sesaat saat koper dilempar oleh sang anak dan kembali naik, namun lebih rendah dari posisi awal saat koper tenggelam seluruhnya
E. Ketinggian laut turun sesaat saat koper dilempar oleh sang anak dan kembali naik, namun lebih tinggi dari posisi awal saat koper tenggelam seluruhnya
Kunci jawaban: "D"
Pada mulanya kapal beserta isinya terapung di atas laut dengan sebagian kapal berada di dalam air laut. Hal ini sesuai dengan hukum Archimedes yang menyatakan bahwa besarnya gaya ke atas sama dengan besar zat cair yang dipindahkan, gaya ke atas inilah yang kemudian menahan kapal laut agar tetap terapung. Peristiwa terapungnya suatu benda dalam zat cair disebabkan karena massa jenis benda lebih kecil daripada massa jenis zat cair, semakin kecil massa jenis benda maka benda tersebut akan semakin terapung
Ketika sebuah koper dilemparkan, untuk beberapa saat berat kapal akan berkurang sehingga gaya ke atas juga akan semakin kecil akibatnya kapal sedikit terangkat dan permukaan air laut sedikit turun. namun ketika koper sudah jatuh ke laut, dengan berat yang sama (setelah koper dilempar) karena massa jenis koper lebih besar daripada massa jenis kapal maka volume koper yang dijatuhkan lebih kecil daripada volume kapal sehingga permukaan air laut akan naik sedikit tetapi lebih rendah dari posisi semula.
Soal nomor 4
Sebuah kalorimeter yang kapasitas kalornya 50 kal/0C berisi 200 gram air yang bersuhu 200C. Kemudian ke dalam kalorimeter itu dimasukkan 100 gram es −100C. Setelah dicapai kesetimbangan termis, massa es yang melebur adalah...
A. 43,75 gram
B. 56,25 gram
C. 62,50 gram
D. 68,25 gram
E. 80,00 gram
Kunci jawaban: "B"
Berdasarkan soal dapat diketahui
Ckal = 50 kal/0C
ma = 200 g
Ta = 200C
mes = 100 g
Tes = -100C
cair = 1 kal/g0C
ces = 0,5 kal/g0C
Les = 80 kal/g
Massa es yang melebur?
Kita asumsikan bahwa suhu awal kalorimeter sama dengan suhu awal air yang berada di dalamnya. Ketika ke dalam kalorimeter tersebut dimasukkan sejumlah es maka terjadi perpindahan kalor dari air dan kalorimeter ke es, karena ditanyakan massa es yang melebur maka kita dapat mengetahui bahwa:
- Tidak semua es mencair
- Hanya sebagian es yang mencair, menunjukkan jumlah kalor yang dilepaskan oleh air dan kalorimeter tidak cukup untuk mencairkan seluruh es, meskipun suhunya mencapai 0 0C
- Batas akhir Suhu akhir air sistem adalah 0 0C
Qlepas = Qserap
mair . cair . ∆Tair + Ckal . ∆Tkal = mes . ces . ∆Tes + mes . Les
200 . 1 . (20 – 0) + 50 . (20 – 0) = 100 . 0,5 . (0 – (-10)) + mes . 80
4000 + 1000 = 500 + mes . 80
4500 = mes . 80
mes = 56,25 gram
Soal nomor 5
Sebuah bola tenis bermassa 100 gram dilemparkan tegak lurus ke tembok dengan kecepatan 5 m/s. Bola tersebut menumbuk dinding selama 0,25 detik. Jika kecepatan bola setelah dipantulkan adalah 15 m/s, berapakah besar gaya yang diberikan tembok terhadap bola tersebut?
A. 2 N
B. 4 N
C. 5 N
D. 7,5 N
E. 8 N
Kunci jawaban: "E"
Berdasarkan soal dapat diketahui
m = 100 gram = 0,1 kg
v1 = 5 m/s
∆t = 0,25 s
v2 = -15 m/s (berlawanan arah karena memantul)
F .... ?
Soal tersebut tentang hubungan antara impuls dan momentum, sesuai dengan persamaan berikut
I = ∆p
F . ∆t = m . ∆v
F . ∆t = m (v2 – v1)
F . 0,25 = 0,1 ((-15) – 5)
F . 0,25 = -2
F = - 8 N
Tanda negatif menunjukkan arah gaya searah dengan kecepatan akhir benda setelah menumbuk tembok
Soal nomor 6
Kereta api bergerak dengan laju 72 km/jam menuju stasiun sambil membunyikan peluitnya. Bunyi peluit kereta api tersebut terdengar oleh kepala stasiun dengan frekuensi 680 Hz. Jika kelajuan bunyi di udara 340 m/s, maka frekuensi peluit kereta api tersebut adalah ....
A. 640 Hz
B. 680 Hz
C. 700 Hz
D. 720 Hz
E. 760 Hz
Kunci jawaban: "A"
Berdasarkan soal dapat diketahui
vS = 72 km/jam = 20 m/s (mendekati)
fP = 680 Hz
v = 340 m/s
fS ... ?
persamaan untuk efek doppler pada soal di atas dapat ditulis
Jurus jitu :
Perhatikan bahwa kereta api bergerak mendekati stasiun, sehingga bunyi yang dikeluarkan kereta api akan terdengar lebih keras oleh orang yang berada di stasiun. Hal ini menunjukkan frekuensi bunyi yang di dengar oleh orang di stasiun (frekuensi pendengar atau fP) lebih besar daripada frekuensi yang dikeluarkan oleh kereta api (frekuensi sumber atau fS).
Jika kepala stasiun mendengar bunyi peluit dari kereta api dengan frekuensi 680 Hz, maka tentunya frekuensi peluit yang di keluarkan oleh kereta api kurang dari 680 Hz dan berdasarkan pilihan jawaban, kemungkinannya hanya pilihan A
Soal nomor 7
Suatu mesin Carnot mempunyai efisiensi 30% dengan temperature reservoir suhu tinggi sebesar 750 K. Agar efisiensi mesin naik menjadi 50% maka temperature reservoir suhu tinggi harus dinaikkan menjadi…
A. 1.050 K
B. 1.000 K
C. 950 K
D. 900 K
E. 850 K
Kunci jawaban: "A"
Berdasarkan soal dapat diketahui
ηA = 30%
T1A = 750 K
ηB = 50%
T1B = ...?
Hubungan antara efisiensi mesin Carnot dengan suhu reservoir dituliskan dalam persamaan berikut
Karna reservoir temperatur rendah tidak berubah untuk kedua keadaan maka, kita dapat menuliskan persamaan di atas menjadi
(1 – ηA)T1A = (1 – ηB)T1B
Persamaan di atas dapat dihafalkan sebagai rumus cepat menentukan reservoir suhu tinggi ketika efisiensinya berubah atau sebaliknya
(1 – 30%) 750 = (1 – 50%)T1B
(1 – 0,3) 750 = (1 – 0,5) T1B
0,7 . 750 = 0,5 T1B
T1B = 1050 K
Soal nomor 8
Dua buah konduktor (A dan B) terbuat dari bahan yang sama dengan panjang keduanya juga sama. Konduktor A merupakan kawat padat dengan diameter tampang lintang sebesar 1 m. Konduktor B merupakan kawat dengan penampang lintang berlubang dengan diameter dalam 1 m dan diameter luar 2 m. Besar perbandingan nilai hambatan RA/RB adalah....
A. 4
B. 3
C. 2
D. √2
E. 1
Kunci jawaban: "B"
Berdasarkan soal dapat diketahui:
dA = 1 m
dB = 1 m (diameter dalam kawat B)
dB’ = 2 m (diameter luar kawat B)
RA / RB ....?
Persamaan untuk menentukan hambatan kawat adalah
Perhatikan bahwa luas penampang berbanding terbalik dengan hambatan, sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut
Soal nomor 9
Sebuah generator disuplai dengan 2.000 kg/s air yang mengalir melalui turbinnya dengan kelajuan 10 m/s. Jika generator mengubah 80% energi kinetik air menjadi energi listrik, daya listrik yang dihasilkan turbin adalah…
A. 40 kW
B. 80 kW
C. 400 kW
D. 800 kW
E. 4.000 kW
Kunci jawaban: "B"
Berdasarkan soal dapat diketahui
m/t = 2.000 kg/s
v = 10 m/s
η = 80%
P .... ?
Konsep pada soal di atas adalah perubahan energi kinetik menjadi energi listrik dengan efisiensi sebesar 80%, kita dapat menuliskannya dalam persamaan
η Ek = W
η ½ mv2 = Pt
η ½ (m/t) v2 = P
80% ½ (2000) 102 = P
0,8 100000 = P
P = 80.000 Watt
P = 80 kW
Soal nomor 10
Sebuah balok dengan berat 100 Newton diam pada sebuah bidang datar. Kemudian dari waktu t = 0 s sampai t = 5 s balok didorong dengan gaya konstan 40 Newton sejajar bidang datar. Koefisien gesek kinetik dan statis antara balok dan bidang datar berturut-turut adalah 0,2 dan 0,3. Dalam selang waktu antara t = 5s sampai t = 10s balok…
A. Bergerak dengan kecepatan tidak tetap
B. Bergerak dengan kecepatan tetap
C. Bergerak dengan percepatan tidak tetap
D. Bergerak kemudian akhirnya diam
E. Bergerak kemudian berhenti sebelum detik ke 10
Kunci jawaban: "D"
Berdasarkan soal dapat diketahui
F = 40 N
w = 100 N
μk = 0,2
μs = 0,3
soal di atas dapat diilustrasikan sebagai berikut
Percepatan yang dialami benda selama bekerja gaya F
ΣF = m a
F – fk = m a
F – μk w = (w/g) a
40 – 0,2 . 100 = (100/10) a
40 – 20 = 10 a
20 = 10 a
a = 2 m/s2
kecepatan benda setelah bergerak 5 s (sampai di titik B)
vB = vA + at
vB = 0 + 2 . 5
vB = 10 m/s
setelah dari titik B gaya F ditiadakan tetapi masih ada gaya gesek kinetik yang menyebabkan benda mengalami perlambatan hingga berhenti di titik C dengan perlambatan sebesar
ΣF = m a
-fk = m a
-20 = 10 a
a = - 2 m/s2
waktu sampai berhenti kembali
vC = vB – at
0 = 10 – 2t
t = 5 s jadi dibutuhkan waktu 5 detik dari titik B untuk membuat benda kembali berhenti atau dapat dikatakan benda berhenti pada saat t = 10 s jika dihitung dari titik awal A
Soal nomor 11
Pada sebuah bangku bermassa 40 kg diletakkan beban bermassa M seperti pada gambar.
Nilai maksimum M agar sistem masih berada dalam kesetimbangan adalah....
A. 120 kg
B. 100 kg
C. 80 kg
D. 60 kg
E. 40 kg
Kunci jawaban: "A"
Berdasarkan soal di ketahui
mB = 40 kg (massa bangku)
M ... ? (massa beban)
Gaya-gaya yang bekerja pada sistem dapat diilustrasikan sebagai berikut
Karna diinginkan nilai maksimum dari M, maka gaya normal di titik P harus sama dengan nol (NP = 0) atau bangku tidak terangkat di titik P, sehingga kita dapat mencari resultan torsinya dengan poros di titik Q,
Στ = 0 (poros di Q)
τB = τb
wB . RB = wb . Rb
mB . g . RB = mb . g . Rb
mB . RB = mb . Rb
40 . 60 = M . 20
M = 120 kg
Soal nomor 12
Jika m0 massa diam electron dan c laju cahaya di ruang hampa maka electron yang
bergerak dengan kecepatan 0,8c memiliki energi kinetik sebesar…
A. 2 m0c2
B. 5/3 m0c2
C. 4/3 m0c2
D. m0c2
E. 2/3 m0c2
Kunci jawaban: "E"
Berdasarkan soal dapat diketahui
v = 0,8 c
Ek = .... ?
Karna
v = 0,8 c
v = 8/10 c
maka dengan menggunakan hubungan phytagoras, (baca : jurus jitu menyelesaikan soal relativitas khusus)
γ = 10/6
γ = 5/3
jadi energi kinetiknya dapat ditentukan dengan cara>
Ek = (γ – 1) E0
Ek = (5/3 – 1)m0c2
Ek = 2/3 m0c2
Soal nomor 13
Permukaan sebuah lempeng logam natrium disinari dengan seberkas foton berenergi 4,43
eV. Jika fungsi kerja natrium adalah 2,28 eV maka energy kinetic maksimum electron
yang dihasilkan adalah…
A. 2,15 eV
B. 2,28 eV
C. 4,56 eV
D. 6,71 eV
E. 8,86 eV
Kunci jawaban: "A"
Berdasarkan soal dapat diketahui
E = 4,43 eV
W0 = 2,28 eV
EKmaks ...?
Pada efek fotolistrik berlaku persamaan
EKmaks = E – W0
EKmaks = 4,43 – 2,28
EKmaks = 2,15 eV
Soal nomor 14
Dua lampu pijar identik dengan spesifikasi 100 watt, 110 volt, dihubungkan paralel pada
tegangan 110 volt. Daya total kedua lampu adalah…
A. 100 W
B. 125 W
C. 150 W
D. 175 W
E. 200 W
Kunci jawaban: "E"
Karena kedua lampu di pasang paralel maka tegangan yang bekerja pada lampu sama dengan tegangan sumber yakni 110 volt. Sehingga berdasarkan spesifikasinya ketika diberi tegangan 110 volt daya lampu adalah 100 watt,. Jadi daya total kedua lampu sama dengan 100 + 100 = 200 watt
Soal nomor 15
Jumlah muatan dari dua buah muatan q1 dan q2 adalah -6µC. Jika kedua muatan tersebut
dipisahkan sejauh 3 m maka masing-masing muatan akan merasakan gaya listrik sebesar
8mN. Besar q1 dan q2 berturut-turut adalah…
A. -5µC dan -1µC
B. -10µC dan -4 µC
C. -3 µC dan -3 µC
D. -8 µC dan 2 µC
E. -4 µC dan -2 µC
Kunci jawaban: "E"
Berdasarkan soal dapat diketahui
q1 + q2 = -6μC = -6 x 10-6 C
r = 3 m
F = 8 mN = 8 x 10-3 N
q1 dan q2 ...?
karena jumlah kedua muatan adalah negatif, maka muatan-muatan tersebut adalah elektron dan proton, berdasarkan hukum Coulomb kita dapat menuliskan
Berdasarkan soal maka
q1 + q2 = -6 ∙ 10-6
q1 = - q2 -6 ∙ 10-6 ...(2)
Substitusikan persamaan (2) ke persamaan (1)
(-q2 – 6 . 10-6) q2 = 8 . 10-12
-( q2)2 – 6 . 10-6 q2 = 8 . 10-12
q22 + 6 . 10-6 q2 + 8 . 10-12 = 0
(q2 + 4 . 10-6) (q2 + 2 . 10-6) = 0
q2 = - 4 . 10-6 atau q2 = - 2 . 10-6
jika q2 = - 4 . 10-6, maka q1 = - 2 . 10-6
jika q2 = - 2 . 10-6, maka q1 = - 4 . 10-6