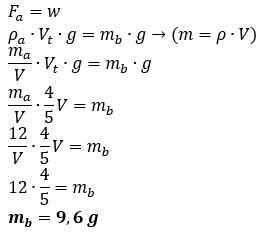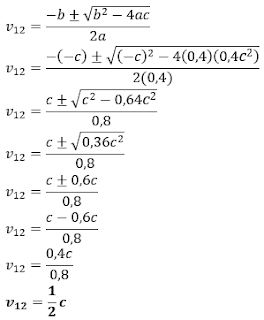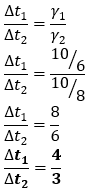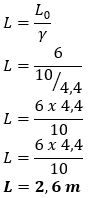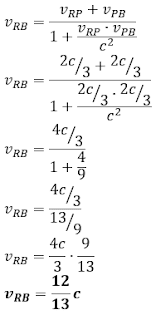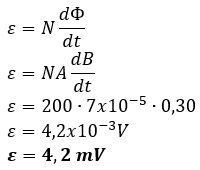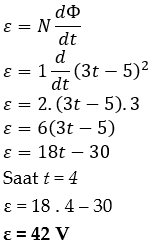LATIHAN SOAL UTBK 2022 - FISIKA | PAKET 2

Untuk mempersiapkan diri bagi siswa/i kelas 12 yang akan mengikuti UTBK tahun 2022, maka pada kesempatan kali ini saya akan memberikan beberapa latihan soal pada mata pelajaran Fisika. Soal – soal yang ada di bawah ini sudah disertai pembahasannya dan dihimpun dari berbagai sumber. Selamat menikmati

Soal nomor 1
Sebuah balok plastik homogen mengapung di suatu bejana air. Seperlima bagian balok berada di atas permukaan air. Jika volume balok V dan massa air sebanyak V tersebut adalah 12 g maka massa balok adalah … g
A. 9,2
B. 9,4
C. 9,6
D. 9,8
E. 10,0
Kunci jawaban: "C"

pembahasan soal nomor 1:

Berdasarkan soal dapat diketahui
V_t = 4/5 V (perhatikan soal 1/5 bagian berada di permukaan, sehingga bagian yang tercelup adalah 4/5V)
m_a = 12 g
m_b ... ?
untuk benda terabung sama dengan

Soal nomor 2
Sebuah balon yang awalnya berisi gas 1 liter ditambahkan gas yang sama sehingga volume balon menjadi 1,2 liter dan massa gas di dalam balon menjadi satu setengah kalinya. Jika suhu gas tetap maka rasio pertambahan tekanan terhadap tekanan awalnya adalah…
A. 0,25
B. 0,33
C. 0,50
D. 0,67
E. 0,75
Kunci jawaban: "A"

pembahasan soal nomor 2:

Berdasarkan soal dapat diketahui
V₁ = 1 liter
V₂ = 1,2 liter
m₂ = 1,5 m1
∆P/P₁ ...?
Untuk gas ideal berlaku persamaan umum
PV = nRT
PV = (m/Mr) RT
PV/m = RT/Mr (konstan)
Dari persamaan di atas kita dapat menggunakan bagian di ruas kiri sebagai persamaan perbandingannya untuk menentukan P₂ yakni

Dengan ∆P = P₂ – P₁, maka rasio perbandingan pertambahan tekanan terhadap tekanan akhirnya dapat ditentukan sebagai berikut

Soal nomor 3
Sebuah bola pejal bermassa M dengan momen inersia I menggelinding pada bidang miring dari keadaan diam dengan ketinggian h. Cara yang dapat dilakukan untuk memperbesar kelajuan linier bola pejal tersebut menjadi dua kalinya adalah ...
A. Memperbesar M menjadi 2M
B. Memperbesar I menjadi 2I
C. Memperbesar I menjadi 4I
D. Memperkecil I menjadi 0,25I
E. Memperbesar h menjadi 4h
Kunci jawaban: "E"

pembahasan soal nomor 3:

Bola menggelinding, berarti bola tersebut melakukan dua gerakan yakni gerak rotasi dan gerak translasi, sehingga memiliki dua jenis energi kinetik yaitu energi kinetik rotasi dan energi kinetik translasi. Untuk bola menggelinding di bidang miring berlaku hukum kekekalan energi sebagai berikut.
EP = EK_T + EK_R
mgh = ½ mv² + ½ I ω²
mgh = ½ mv² + ½ (k mr²) (v/r)²
dimana “k” merupakan konstanta inersia, untuk bola pejal k = 2/5
mgh = 1/2 mv² + 1/2 . 2/5 mv²
gh = 1/2 v² + 1/5 v²
gh = 7/10 v²
v² = 10/7 gh
berdasarkan persamaan di atas maka kita dapat mengetahui bahwa kuadrat kecepatan sebanding dengan ketinggian dan percepatan gravitasi, sehingga agar kecepatannya menjadi dua kali semula dapat dilakukan dengan cara

• Memperbesar ketinggian menjadi 4 kali semula
• Memperbesar percepatan gravitasi menjadi 4 kali semula

Soal nomor 4
Bila perbandingan jari-jari sebuah planet (R_p) dan jari-jari bumi (R_b) adalah 2 : 1, sedangkan massa planet (M_p) dan massa bumi (M_b) berbanding 10 : 1, maka orang yang beratnya di bumi 100 N, di planet menjadi ....
A. 100 N
B. 200 N
C. 250 N
D. 400 N
E. 500 N
Kunci jawaban: "C"

pembahasan soal nomor 4:

Berdasarkan soal dapat diketahui
R_p: R_b = 2 : 1
M_p : M_b = 10 : 1
F_b = 100 N
F_p ... ?
untuk gaya berat (gaya gravitasi) dapat ditentukan dengan persamaan

Berdasarkan persamaan di atas kita dapat mengetahui bahwa gaya berat sebanding dengan massa planet dan berbanding terbalik dengan kuadrat jari-jarinya, sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut

Soal nomor 5
Benda A dan B bermassa sama masing-masing 2 kg saling bertumbukan. Kecepatan sebelum tumbukan adalah v_A = 15i + 30j (m/s) dan v_B = -10i + 5j (m/s). kecepatan benda A setelah tumbukan adalah -5i + 20j (m/s). persentase energi kinetik yang hilang setelah tumbukan adalah ....
A. 10%
B. 20%
C. 40%
D. 60%
E. 80%
Kunci jawaban: "C"

pembahasan soal nomor 5:

Berdasarkan soal dapat diketahui
m_A = m_B = 2 kg
v_A = 15i + 30j
v_B = -10i + 5j
v_A’ = -5i + 20j
persentase energi kinetik setelah tumbukan..?
untuk mengetahui persentase energi kinetik setelah tumbukan, maka kita harus mengetahui kecepatan kedua benda setelah tumbukan dengan menggunakan hukum kekekalan momentum sebagai berikut
m_A v_A + m_B v_B = m_A v_A’ + m_B v_B’
v_A + vB = v_A’ + vB’ (15i + 30j) + (-10i + 5j) = (-5i + 20j) + v_B’
(15 - 10 + 5)i + (30 + 5 – 20)j = v_B’
v_B’ = 10i + 15j (m/s)

Menentukan besar kuadrat kecepatan masing-masing benda
v_A² = 15² + 30²
v_A² = 225 + 900
v_A² = 1125

v_B² = (-10)² + 5²
v_B² = 100 + 25
v_B² = 125

v_A’² = (-5)² + 20²
v_A’² = 25 + 400
v_A’² = 425

v_B’² = 10² + 15²
v_B’² = 100 + 225
v_B’2 = 325
Menentukan energi kinetik awal
EK₀ = EK_A + EK_B
EK₀ = ½ m_A v_A² + ½ m_B v_B²
EK₀ = ½ m (v_A² + v_B²)
EK₀ = ½ . 2 (1125 + 125)
EK₀ = 1250 J

Menentukan energi kinetik akhir
EK’ = EK_A’ + EK_B’
EK’ = ½ m_A v_A’² + ½ m_B v_B’²
EK’ = ½ m (v_A’² + v_B’²)
EK’ = ½ 2 (425 + 325)
EK’ = 750 J

Menentukan jumlah energi kinetik yang hilang ∆EK = EK0 – EK’
∆EK = 1250 – 750
∆EK = 500 J

Persentase kehilangan energi kinetik
η = (∆EK/EK0)*100%
η = (500/1250)*100%
η = 40%

Soal nomor 6
empat buah muatan masing-masing 10μC, 20μC, -30μC, dan 40μC, ditempatkan pada titik sudut sebuah empat persegi panjang dengan sisi 60 cm, 80 cm. potensial listrik pada titik tengah empat persegi panjang tersebut adalah ....
A. 150 kV
B. 360 kV
C. 720 kV
D. 1440 kV
E. 2880 kV
Kunci jawaban: "C"

pembahasan soal nomor 6:

Soal di atas dapat diilustrasikan sebagai berikut!

Panjang diagonal persegi panjang
d² = 80² + 60²
d = 100 cm (pasangan phytagoras, 60 , 80 , 100)
jarak muatan ke titik tengah (P)
r = ½ d
r = ½ . 100
r = 50 cm
r = 0,5 m

karena potensial listrik merupakan besaran skalar, maka untuk menentukan potensial di titik tengahnya dapat dilakukan dengan menjumlahkannya, tapi perhatikan jenis muatan yang digunakan. Jika muatan positif menghasilkan potensial positif, dan jika muatan negatif menghasilkan potensial negatif. Jadi potensial listrik di titik P adalah

Soal nomor 7
Pipa organa terbuka yang panjangnya 25 cm menghasilkan frekuensi nada dasar sama dengan frekuensi yang dihasilkan oleh dawai yang panjangnya 150 cm. Jika cepat rambat bunyi di udara 340 m/s dan cepat rambat gelombang transversal pada dawai 510 m/s maka dawai menghasilkan:
A. nada dasar
B. nada atas pertama
C. nada atas kedua
D. nada atas ketiga
E. nada atas keempat
Kunci jawaban: "D"

pembahasan soal nomor 7:

berdasarkan soal dapat diketahui
L_P = 25 cm = 0,25 m
L_D = 150 cm = 1,5 m
v_P = 340 m/s
v_D = 510 m/s
nada pada dawai, ketika nada dasar pada pipa organa terbuka ...?
frekuensi nada dasar pipa organa terbuka berlaku persamaan
f = v_P/2L_P
persamaan umum frekuensi pada dawai
f = (n + 1)v_D/2L_D ... ( n = 0, 1, 2, 3, ... )
karena frekuensinya sama, maka kedua persamaan di atas dapat ditulis

n = 0 → nada dasar
n = 1 → nada atas pertama
n = 2 → nada atas kedua
n = 3 → nada atas ketiga

Soal nomor 8
Susunan tiga buah hambatan yang besarnya sama menghasilkan hambatan 2 . Jika susunanya diubah, maka dapat dihasilkan hambatan 1 . Besar hambatan tersebut adalah.....
A. 1 Ω
B. 2 Ω
C. 3 Ω
D. 4 Ω
E. 5 Ω
Kunci jawaban: "C"

pembahasan soal nomor 8:

Tiga hambatan sama besar jika dirangkai paralel hasilnya 1 Ω adalah
Rp = n/R
R = n/Rp
R = 3/1
R = 3 Ω

3 buah hambatan 3 Ω, Untuk menghasilkan hambatan total sebesar 2 Ω maka 2 resitor di rangkai seri kemudian di rangkai paralel dengan resistor yang ketiga.
Rs = 3 + 3 = 6 Ω
1/Rp = 1/6 + 1/3
1/Rp = 1/6 + 2/6
1/Rp = 3/6
Rp = 2 Ω

Soal nomor 9
Sebuah kubus memiliki volume sejati 1000 cm Volume kubus tersebut menurut seorang pengamat yang bergerak dengan kecepatan 0,8 c relatif terhadap kubus dalam arah sejajar salah satu rusuknya adalah...
A. 100 cm³
B. 300 cm³
C. 400 cm³
D. 500 cm³
E. 600 cm³
Kunci jawaban: "E"

pembahasan soal nomor 9:

Berdasarkan soal dapat diketahui
V₀ = 1000 cm
v = 0,8 c
V...?
Ketika kubus di amati oleh pengamat yang bergerak searah dengan salah satu rusuknya, maka terjadi perubahan panjang dari rusuk tersebut (yang searah dengan gerak pengamat). Sesuai dengan persamaan pemekaran panjang yakni
L = L₀/γ ,
maka persamaan untuk Volume relativistik adalah
V = V₀/γ
Untuk pengamat yang bergerak dengan kecepatan
v = 0,8 c
v = 8/10 c,
maka dengan menggunakan konsep phytagoras kita dapat langsung menentukan nilai γ yakni
γ = 10/6, sehingga
V = 1000 . 6/10
V = 600 cm³

Soal nomor 10
Sebuah tali digetarkan dengan frekuensi 5 Hz menghasilkan gelombang beramplitudo 12 cm dan kelajuan gelombang 20 m/s. Dari pernyataan berikut yang sesuai dengan gelombang yang dihasilkan oleh getaran tali adalah....
1) Frekuensi anguler gelombang 31,4rad/s
2) Panjang gelombang 4 m
3) Persamaan gelombang 0,12 sin 2π (0,25 x - 5 t) m
4) Angka gelombang adalah 1,57 m

A. Jika (1), (2), dan (3) benar
B. Jika (1) dan (3) benar
C. Jika (2) dan (4) benar
D. Jika hanya (4) yang benar
E. Jika semuanya benar
Kunci jawaban: "E"

pembahasan soal nomor 10:

Berdasarkan soal dapat diketahui
f = 5 Hz
A = 12 cm
v 20 m/s

Tips :
Untuk mengerjakan soal tipe pernyataan, sebenarnya kita tidak harus membuktikan semua pernyataan atau harus dimulai dari pernyataan pertama. Kita bisa memulai dengan membuktikan pernyataan yang paling mudah untuk dibuktikan (bisa dibuktikan benar atau salah) kemudian mencocokkan dengan pilihan jawabannya.

Pernyataan 2
v = f λ
20 = 5 λ
λ = 4 (benar)
perhatikan pilihan A, C, dan E

pernyataan 1
ω = 2π f
ω = 2 . 3,14 . 5
ω = 31,4 rad/s (benar)
perhatikan pilihan A dan E

pernyataan 4
k = 2π/λ
k = 2 . 3,14 / 4
k = 1,57 (benar)
perhatikan pilihan E

Soal nomor 11
Beta berlari menjauhi sebuah mobil yang mengeluarkan suara keras, sehingga kecepatan relatif Beta terhadap mobil adalah nol. Apabila mobil bergerak dengan kecepatan 10 m/s dan frekuensi bunyi yang dikeluarkan mobil 300 Hz, maka frekuensi yang diterima Beta adalah ….
A. 280 Hz
B. 300 Hz
C. 330 Hz
D. 340 Hz
E. 350 Hz
Kunci jawaban: "B"

pembahasan soal nomor 11:

Perhatikan bahwa kecepatan relatif beta terhadap mobil sama dengan nol, maka dapat dikatakan bahwa beta bergerak dengan besar kecepatan dan arah kecepatannya sama dengan mobil, sehingga kita dapat mengilustrasikan soal di atas seperti berikut

Tips :
Perhatikan ilustrasi di atas, terlihat sumber mendekati pendengar sehingga ia ingin suara terdengar lebih keras dan pada persamaan efek doppler sumber sebagai penyebut (di bawah) sehingga ia harus bernilai minimal (negatif), sedangkan pendengar juga ingin menjauhi sumber sehingga ia ingin suara terdengar lebih pelan dan pada persamaan efek doppler sumber bertindak sebagai pembilang (di atas) sehingga ia harus bernilai minimal (negatif).
Persamaan efek dopplernya dapat dituliskan

Soal nomor 12
Tiga buah kapasitor disusun paralel dalam rangkaian sesuai gambar berikut.

Total muatan tersimpan dalam kapasitor adalah ….
A. 1 C
B. 2 C
C. 3 C
D. 4 C
E. 5 C
Kunci jawaban: "E"

pembahasan soal nomor 12:

Perhatikan pada ketiga kapasitor di atas, di rangkai paralel sehingga kapasitas kapasitor total pada rangkaian adalah...
C_tot = C₁ + C₂ + C₃
C_tot = 1 + 2 + 2
C_tot = 5 F
Muatan total dalam rangkaian
Q = C . V
Q = 5 . 1
Q = 5 C

Soal nomor 13
li memiliki luas penampang sama dan modulus Young berbeda. Tali pertama memiliki panjang awal 𝑙, sementara tali kedua memiliki panjang awal 2𝑙. Perbandingan modulus Young tali kedua dengan tali pertama adalah 3:1. Bila kedua tali disambung dan digantungi beban bermassa 𝑀, maka pertambahan panjang total tali adalah 0,25𝑙. Pertambahan panjang tali pertama adalah ….
A. 0,05𝑙
B. 0,10𝑙
C. 0,08𝑙
D. 0,15𝑙
E. 0,20𝑙
Kunci jawaban: "D"

pembahasan soal nomor 13:

Berdasarkan soal kita dapat mengetahui
L₁ = 𝑙
L₂ = 2 𝑙
E₂ : E₁ = 3 : 1
∆L_tot = 0,25 𝑙
∆L₁ ... ?
Soal di atas dapat diilustrasikan sebagai berikut

Berdasarkan persamaan modulus Young
E = FL/A∆L
Maka kita dapat mengetahui bahwa
Modulus Young sebanding dengan panjang awal
Modulus Young berbanding terbalik dengan pertambahan panjang
Sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut

Dimana
∆L₁ + ∆L₂ = 0,25l
Maka
∆L₁ = (3/5) . 0,25l
∆L₁ = 0,15l

Soal nomor 14
Elektron memiliki muatan negatif sebesar 1,6 × 10⁻¹⁹ dan bergerak sepanjang sumbu 𝑥 dengan kecepatan 5 × 10⁵ m/s. Elektron bergerak melewati medan magnet 5 T sesuai gambar berikut.

Besar dan arah gaya Lorentz yang bekerja terhadap elektron adalah ….
A. 4 × 10⁻¹⁴ N ke atas
B. 4 × 10⁻¹⁴ N ke bawah
C. 4 × 10⁻¹³ N ke atas
D. 4 × 10⁻¹³ N ke bawah
E. 4 × 10⁻¹² N ke atas
Kunci jawaban: "C"

pembahasan soal nomor 14:

Berdasarkan soal dapat diketahui
Q = 1,6 . 10^-19 C
v = 5 . 10⁵
B = 5 T
F (besar dan arah) ...?
Untuk muatan negatif (elektron) Arah gaya Lorentz dapat ditentukan dengan kaidah tangan kiri

• Ibu jari sebagai arah kecepatan
• Telunjuk sebagai arah medan magnet
• Jari tengah sebagai arah gaya lorentz

Sehingga arah gaya lorentznya adalah ke bawah (perhatikan pilihan A, C, dan E)
Besar gaya lorentz dapat ditentukan dengan persamaan
F = B q v
F = 5 x 5 . 10⁵ x 1,6 . 10^-19
F = 40 . 10^-14
F = 4 . 10^-13 N

Soal nomor 15
Sebuah benda bermassa 𝑀 = 10 kg terikat pada tali yang terhubung dengan katrol tak bermassa. Dari katrol hingga ujung, tali memiliki kemiringan 𝜃 = 30⁰. Ujung tali ditarik dengan gaya sebesar 𝐹

Apabila sistem tersebut diam, kita dapat menyimpulkan bahwa ….
A. 𝐹 = 100 N
B. 𝐹𝑥 = 100 N
C. 𝐹𝑦 = 100 N
D. 𝐹𝑦 + 𝑇 = 100 N
E. 𝐹𝑥 + 𝑇 = 100 N
Kunci jawaban: "A"

pembahasan soal nomor 15:

Karena katrol dalam keadaan diam, maka sistem di atas dapat kita tinjau dalam sistem 1 dimensi, sehingga kita tidak perlu menguraikannya menjadi Fx dan Fy, dalam keadaan diam berlaku persamaan
F = w
F = m . g
F = 10 . 10
F = 100 N

Soal dan Pembahasan | Teori Relativitas Khusus Einsten (Fisika Kelas 12)

Soal dan pembahasan : relativitas khusus Einstein ditulis sebagai bahan belajar atau referensi untuk membuat soal-soal ulangan harian, yang mana materi relativitas khusus Einstein dipelajari oleh siswa pada kelas 12 semester genap. Sebagian besar siswa menganggap bahwa materi relativitas khusus Einstein sebagai salah satu materi fisika yang sulit dipahami, oleh karena itu dengan artikel ini semoga dapat menambah pemahaman kepada para pembaca dalam memahami materi relativitas khusus Einstein. Sebelum melanjutkan membaca soal dan pembahasan relativitas khusus Einstein, silahkan dibaca juga artikel kami yang berjudul Jurus Jitu : Menyelesaikan Soal Relativitas Khusus Einstein, disana para pembaca akan menemukan beberapa tips dan trik yang saya sebut jurus jitu sebagai hasil apa yang saya peroleh dalam mempelajari materi ini dan saya gunakan untuk membuat pembahasan dalam soal-soal di bawah ini. Selamat membaca.

Soal nomor 1

Sebuah partikel yang bergerak dengan kelajuan 0,3c terhadap kerangka acuan laboratorium memancarkan sebuah elektron searah dengan kecepatan 0,3c relatif terhadap partikel. Laju elektron tadi menurut kerangka acuan laboratorium paling dekat nilainya dengan ...
A. 0,32c
B. 0,51c
C. 0,66c
D. 0,76c
E. 0,90c
Kunci jawaban: "B"

pembahasan soal nomor 1:

Soal di atas dapat diilustrasikan sebagai berikut

v_PL = 0,3c (kecepatan partikel relatif terhadap lab)
v_EP = 0,3c (kecepatan elektron relatif terhadap partikel)
v_EL = ...? (kecepatan elektron relatif terhadap lab)
persamaan umum untuk penjumlahan relativistiknya dapat ditulis

Soal nomor 2

Dua roket saling mendekat dengan kelajuan sama relatif terhadap bumi. jika kelajuan relatif roket satu terhadap roket lainnya adalah 0,80c maka kelajuan roket adalah ....
A. 0,40c
B. 0,50c
C. 0,60c
D. 0,70c
E. 0,75c
Kunci jawaban: "B"

pembahasan soal nomor 2:

Soal di atas dapat diilustrasikan sebagai berikut :

v_1B = v (kecepatan pesawat 1 relatif terhadap bumi)
v_2B = -v (kecepatan pesawat 2 relatif terhadap bumi)
v₁₂ = 0,8c (kecepatan pesawat 1 relatif terhadap pesawat 2)
v ... ?
persamaan umum penjumlahan relativitasnya dapat ditulis

Untuk persamaan di atas kita dapat menggunakan rumus abc, dimana a = 0,4, b = (-c), dan c = 0,4c² seperti berikut ini

Soal nomor 3

Perbandingan dilasi waktu untuk sistem yang bergerak pada kecepatan 0,8c (c = cepat rambat cahaya) dengan sistem yang bergerak dengan kecepatan 0,6c adalah ....
A. 3 : 4
B. 4 : 3
C. 9 : 2
D. 9 : 16
E. 16 : 9
Kunci jawaban: "B"

pembahasan soal nomor 3:

Berdasarkan soal dapat diketahui
v₁ = 0,8c
v₂ = 0,6c
Δt₁ : Δt₂ = ... ?
Persamaan untuk dilatasi waktu adalah
Δt = γ Δt₀ ... (1)
Dengan menggunakan kecepatan dan konsep phytagoras (baca jurus jitu) kita dapat menentukan nilai γ sebagai berikut:
v₁ = 0,8c
v₁ = 8/10 c
sisi siku-siku = 8
sisi miring = 10
sisi siku-siku lainnya = 6
γ₁ = 10/6
v₂ = 0,6c
v₂ = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya = 8
γ₂ = 10/8
berdasarkan persamaan (1) kita dapat menuliskan persamaan perbandingannya

Soal nomor 4

Sebuah cincin berbentuk lingkaran diam dalam kerangka S seperti ditunjukkan dalam gambar.

Bentuk cincin menurut pengamat O’ adalah ....

Kunci jawaban: "C"

pembahasan soal nomor 4:

Karena pengamat O’ berada pada kerangka acuan S’ yang bergerak dalam arah sumbu x dengan kecepatan mendekati kecepatan cahaya, maka jari – jari lingkaran yang sejajar dengan sumbu x akan mengalami kontraksi panjang sehingga panjangnya menjadi lebih kecil dari panjang jari-jari semula. Oleh karena itu bentuknya akan menyempit dalam arah vertikal seperti pada gambar C

Soal nomor 5

Sebuah pesawat ruang angkasa yang panjangnya 6 m bergerak dengan kecepatan 2,7 x 10⁸ m/det. Panjang pesawat menurut pengamat yang diam di bumi adalah ....
A. 1,9 m
B. 2,6 m
C. 4,0 m
D. 8,0 m
E. 19 m
Kunci jawaban: "B"

pembahasan soal nomor 5:

L₀ = 6m
v = 2,7 x 10⁸ m/s
v = (2,7 x 10⁸)/3 x 10⁸
v = 0,9c
L ... ?
Menentukan nilai “γ”
v = 0,9c
v = 9/10 c
sisi siku-siku = 9
sisi miring = 10
sisi siku-siku lainnya
x² = 10² – 9²
x² = 100 – 81
x² = 19
x = √19
x = 4,4 m
jadi nilai γ
γ = 10/4,4

persamaan untuk relativitas panjang

Soal nomor 6

Sebuah kubus memiliki volume sejati 1000 cm³. Volum kubus tersebut menurut seseorang pengamat yang bergerak dengan kecepatan 0,8c relatif terhadap kubus dalam arah sejajar salah satu rusuknya adalah ....
A. 100 cm³
B. 300 cm³
C. 400 cm³
D. 500 cm³
E. 600 cm³
Kunci jawaban: "E"

pembahasan soal nomor 6:

Berdasarkan soal dapat diketahui
V₀ = 1000 cm³
v = 0,8c
V ... ?
Menentukan nilai “γ”
v = 0,8c
v = 8/10 c
sisi siku-siku = 8
sisi miring = 10
sisi siku-siku lainnya (x) = 6
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/6

karena kubus bergerak sejajar dengan salah satu rusuknya, maka hanya satu rusuk yang mengalami konstraksi panjang, sehingga hubungan antara volume diam dengan volume bergerak kubus dapat ditulis
V₀ = L₀³ (Volume diam kubus)
V = L³ (Volume bergerak kubus)
V = L . L²
V = L₀ / γ . L₀²
V = L₀³ / γ
V = V₀ / γ
V = 1000 / (10/6)
V = 1000 . 6 / 10
V = 600 cm³

Soal nomor 7

Sebuah benda mempunyai massa diam 2 kg. Bila benda bergerak dengan kecepatan 0,6c, maka massanya akan menjadi ....
A. 2,6 kg
B. 2,5 kg
C. 2,0 kg
D. 1,6 kg
E. 1,2 kg
Kunci jawaban: "B"

pembahasan soal nomor 7:

Berdasarkan soal dapat diketahui
m₀ = 2 kg
v = 0,6c
m ... ?
Menentukan nilai “γ”
v = 0,6c
v = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya (x) = 8
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/8

persamaan untuk massa relativistik adalah
m = γm₀
m = (10/8) 2
m = 2,5 kg

Soal nomor 8

Sebuah kubus dengan massa jenis 3200 kg/m³ bergerak dengan kelajuan 0,6c sejajar salah satu rusuknya terhadap pengamat O. Massa jenis kubus itu bila diukur oleh pengamat O adalah (dalam kg/m³) ....
A. 2560
B. 3200
C. 4000
D. 5000
E. 5400
Kunci jawaban: "D"

pembahasan soal nomor 8:

Berdasarkan soal dapat diketahui
ρ₀ = 3200 kg/m³
v = 0,6c
ρ .... ?
Menentukan nilai “γ”
v = 0,6c
v = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya (x) = 8
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/8

Hubungan antara massa jenis relativistik (ρ) dan massa jenis diamnya (ρ₀) dapat ditentukan dengan persamaan berikut ini

Soal nomor 9

Agar energi kinetik benda bernilai 20% energi diamnya dan c adalah kelajuan cahaya dalam ruang hampa, maka benda harus bergerak dengan kelajuan ....
A. c/4
B. c/2
C. c√11 /6
D. c√2 /3
E. c√13 /6
Kunci jawaban: "C"

pembahasan soal nomor 9:

Berdasarkan soal dapat diketahui
EK = 20 E₀
v ... ?
persamaan energi kinetik relativistik dapat ditulis
EK = (γ – 1)E₀
20%E0 = (γ – 1)E₀
0,2 = γ – 1
γ = 1,2
γ = 12/10, dimana
12 merupakan sisi miring
10 merupakan sisi siku-siku
Dengan menggunakan konsep phytagoras kita dapat menentukan sisi siku-siku lainnya yakni
x² = 12² – 10²
x² = 144 – 100
x² = 44
x = 2√11
sehingga kecepatan benda adalah

Soal nomor 10

Jika energi total proton adalah empat kali energi diamnya, maka kelajuan proton adalah ... (c = kecepatan cahaya)
A. 2/3 √2 c
B. 1/4 √15 c
C. 3/5 √3 c
D. 1/2 √11 c
E. 1/6 √5 c
Kunci jawaban: "B"

pembahasan soal nomor 10:

Berdasarkan soal dapat diketahui
E = 4E₀
v .... ?
persamaan energi total relativistik dapat ditulis
E = γE₀
4E₀ = γE₀
γ = 4
γ = 4/1, dimana
4 merupakan sisi miring
1 merupakan sisi siku-siku
Dengan menggunakan konsep phytagoras kita dapat menentukan sisi siku-siku lainnya
x² = 4² – 1²
x² = 16 – 1
x² = 15
x = √15
sehingga kecepatan benda tersebut adalah

Soal nomor 11

Sebuah pesawat bergerak dengan kecepatan 0,6c terhadap bumi. dari pesawat ditembakkan peluru dengan kecepatan 0,4c searah dengan pesawat. kecepatan peluru terhadap bumi adalah ....
A. c
B. 0,8c
C. 0,6c
D. 0,5c
E. 0,2c
Kunci jawaban: "B"

pembahasan soal nomor 11:

Soal di atas dapat diilustrasikan sebagai berikut

v_PB = 0,6c (kecepatan pesawat relatif terhadap bumi)
v_RP = 0,4c (kecepatan peluru relatif terhadap pesawat)
v_RB = ... ? (kecepatan peluru relatif terhadap bumi)
tuliskan persamaan umumnya sebagai berikut

Soal nomor 12

Pada sebuah dinding tegak terdapat gambar sebuah segitiga sama sisi dengan panjang sisi 3 . Seandainya gambar tersebut dilihat oleh orang yang sedang berada di dalam pesawat yang bergerak sejajar dengan dinding dengan kecepatan 0,60c, maka luas segitiga tersebut adalah ....

A. √3 ms²
B. 1,8√2 m²
C. 1,8√3 m²
D. 2,4√3 m²
E. 3√3 m²
Kunci jawaban: "C"

pembahasan soal nomor 12:

Menentukan nilai “γ”
v = 0,6c
v = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya (x) = 8
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/8

karena pesawat bergerak sejajar dengan dinding, maka bagian segitiga yang mengalami kontraksi panjang adalah tinggi segitiga tersebut. perhatikan ilustrasi berikut
gambar 12
tinggi diam segitiga sama sisi adalah
t₀² = 3² – 1,5²
t₀² = (2 . 1,5)² – 1,5²
t₀² = (22 – 1) 1,5²
t₀² = (4 – 1) . 1,5²
t₀² = 3 . 1,5²
t₀ = 1,5√3 m
hubungan antara luas diam dengan luas bergeraknya adalah
gambar 12a

Soal nomor 13

Ada dua anak kembar A dan B. A berkelana di antariksa dengan pesawat antariksa yang berkecepatan 0,8c. setelah 12 tahun berkelana A pulang ke bumi. menurut B perjalanan A telah berlangsung selama ...
A. 20 tahun
B. 15 tahun
C. 12 tahun
D. 10 tahun
E. 8 tahun
Kunci jawaban: "A"

pembahasan soal nomor 13:

Berdasarkan soal dapat diketahui
Δt₀ = 12 tahun
v = 0,8c
Δt ... ?
Menentukan nilai “γ”
v = 0,8c
v = 8/10 c
sisi siku-siku = 8
sisi miring = 10
sisi siku-siku lainnya (x) = 6
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/6
persamaan dilatasi waktu adalah
Δt = γΔt0
Δt = 10/6 Δt0
Δt = 10/6 . 12
Δt = 20 tahun

Soal nomor 14

Bila laju partikel 0,6 c, maka perbandingan massa relativistik partikel itu terhadap massa diamnya adalah ....
A. 5 : 3
B. 25 : 9
C. 5 : 4
D. 25 : 4
E. 8 : 5
Kunci jawaban: "C"

pembahasan soal nomor 14:

Berdasarkan soal dapat diketahui
v = 0,6c
m : m₀ = ...?
Menentukan nilai “γ”
v = 0,6c
v = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya (x) = 8
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/8

persamaan untuk massa relativistik adalah
m = γ m₀
m : m₀ = γ
m : m₀ = 10 : 8
m : m₀ = 5 : 4

Soal nomor 15

Sebuah elektron bergerak dengan kecepatan v = 1/12 c √23 . pernyataan yang benar adalah ....
(1) Massa geraknya = 12/11 x massa diamnya
(2) Energi totalnya = 12/11 x energi diamnya
(3) Energi kinetiknya = 1/11 x energi diamnya
(4) Energi totalnya = 11/12 x energi diamnya
Kunci jawaban: “A” (1, 2, 3 benar)

pembahasan soal nomor 15:

Berdasarkan soal dapat diketahui
v = 1/12 c √23

menentukan nilai γ
v = √23/12 c , dimana
√23 merupakan sisi siku-siku
12 merupakan sisi miring
Dengan menggunakan konsep phytagoras kita dapat menentukan panjang sisi siku-siku satunya sebagai berikut
x² = 12² – (√23)²
x² = 144 – 23
x² = 121
x = 11
sehingga nilai γ adalah
γ = 12/11

persamaan massa relativistik
m = γ m₀
m = 12/11 m₀
pernyataan 1 benar

persamaan energi relativistik
EK = (γ – 1) E₀
EK = (12/11 – 1) E₀
EK = 1/11 E₀
Pernyataan 3 benar

EKtot = γE₀
EKtot = 12/11 E₀
Pernyataan 2 benar dan pernyataan 4 salah

Soal nomor 16

Sebuah pesawat mempunyai massa diam m₀ bergerak dengan kecepatan mendekati kecepatan cahaya sehingga massanya menjadi 1 ¼ x massa diamnya. Jika kecepatan cahaya c, maka energi kinetik benda itu adalah ....
A. 0,25 m₀c²
B. 0,5 m₀c²
C. m₀c²
D. 1,25 m₀c²
E. 1,5 m₀c²
Kunci jawaban: "A"

pembahasan soal nomor 16:

Berdasarkan soal dapat ditulis
m = 1 ¼ m₀
m = 5/4 m₀
EK ...?
Berdasarkan persamaan untuk massa relativistik
m = γ m₀
maka kita dapat mengetahui bahwa
γ = 5/4

persamaan energi relativistik adalah
EK = (γ – 1) E₀
EK = (5/4 – 1)m₀c²
EK = ¼ m₀c²
EK = 0,25 m₀c²

Soal nomor 17

Agar energi kinetik benda bernilai 25% energi diamnya dan c adalah kecepatan cahaya dalam ruang hampa, maka benda harus bergerak dengan kelajuan ....
A. c/4
B. c/2
C. 3c/5
D. 3c/4
E. 4c/5
Kunci jawaban: "C"

pembahasan soal nomor 17:

Berdasarkan soal dapat diketahui
EK = 25% E₀
EK = 0,25 E₀
v ... ?
persamaan untuk energi relativistik
EK = (γ – 1) E₀
0,25 E₀ = (γ – 1) E₀
0,25 = γ – 1
γ = 1,25
γ = 5/4, dimana
sisi siku-siku = 4
sisi miring = 5
sisi siku-siku lainnya (x) = 3
(pasangan triple phytagoras)
Jadi besar kecepatan v
v = 3/5 c

Soal nomor 18

Periode suatu pendulum di muka bumi besarnya 3,0 detik. Bila pendulum tersebut diamati oleh seseorang yang bergerak relative terhadap bumi dengan kecepatan 0,95c, maka periode pendulum tersebut dalam detik adalah ....
A. 0,5
B. 1,5
C. 9,6
D. 15
E. 300
Kunci jawaban: "D"

pembahasan soal nomor 18:

Δt₀ = 3,0 s
v = 0,95c
Δt ... ?
menentukan nilai γ
v = 0,95c
v = 95/100 c , dimana
95 merupakan sisi siku-siku
100 merupakan sisi miring
Dengan menggunakan konsep phytagoras kita dapat menentukan panjang sisi siku-siku satunya sebagai berikut
x² = 100² – 95²
x² = 10000 – 9025
x² = 975
x² = √975
x = 31,22

sehingga nilai γ adalah
γ = 100/31,22
γ = 3,2
Persamaan relativitas dilatasi waktu
Δt = γ Δt₀
Δt = 3,2 . 3,0
Δt = 9,6 s

Soal nomor 19

Sebuah pesawat bergerak dengan laju relativistic v. sebuah peluru bermassa diam m ditembakkan searah dengan pesawat dengan laju v relatif terhadap pesawat. jika v = 2/3 c dengan c adalah laju cahaya, maka menurut pengamat di bumi energi total peluru tersebut adalah ....
A. 10mc²/5
B. 11mc²/5
C. 12mc²/5
D. 13mc²/5
E. 15mc²/5
Kunci jawaban: "D"

pembahasan soal nomor 19:

Karna pengamat merupakan orang yang diam di bumi, maka energi kinetiknya juga berdasarkan orang yang diam di bumi, untuk itu kita perlu menentukan besar kecepatan peluru relatif terhadap bumi. Soal di atas dapat diilustrasikan sebagai berikut

v_PB = 2c/3 (kecepatan pesawat relatif terhadap bumi)
v_RP = 2c/3 (kecepatan peluru relatif terhadap pesawat)
v_RB = ... ? (kecepatan peluru relatif terhadap bumi)
tuliskan persamaan umumnya sebagai berikut

Menentukan nilai “γ”
v = 12/13 c
sisi siku-siku = 12
sisi miring = 13
sisi siku-siku lainnya (x) = 5
(pasangan triple phytagoras)
jadi nilai γ
γ = 13/5

menentukan energi total
Etot = γ E₀
Etot = 13mc²/5

Soal nomor 20

Sebuah partikel bermassa diam m0 bergerak sedemikian rupa sehingga energi totalnya adalah 2 kali energi diamnya. Partikel ini menumbuk partikel diam yang bermassa m0 dan keduanya membentuk partikel baru. Momentum partikel baru adalah ....
A. 3√2 m₀c
B. 3 m₀c
C. 2 m₀c
D. √3 /3 m₀c
E. √3 m₀c
Kunci jawaban: "E"

pembahasan soal nomor 20:

Berdasarkan soal dapat diketahui
Etot = 2 E₀
p ... ?
persamaan untuk relativitas energi dan momentum adalah
Etot² = E₀² + (pc)²
(2E₀)² = E₀² + (pc)²
4E₀² = E₀² + (pc)²
3E₀² = (pc)²
pc = √3 E₀
pc = √3 m₀c²
p = √3 m₀c

demikian beberapa soal dan pembahasan tentang materi Teori Relativitas Khusus Einstein, semoga bisa memberikan manfaat kepada para pembaca. jika ada yang ingin bertanya atau menyampaikan saran dan kritik bisa ditulis di kolom komentar

Induksi Elektromagnetik | Soal dan Pembahasan (Fisika Kelas 12 - part 1)

Induksi elektromagnetik merupakan salah satu materi yang ada di kelas 12 semester 1, materi ini sebenarnya tidak terlalu sulit untuk dipahami karena berkaitan dengan kehidupan sehari – hari sehingga dapat diilustrasikan. Untuk materi induksi elektromagnetik nanti akan saya tulis, ditunggu ya. Pada kesempatan kali ini saya akan membahas beberapa soal tentang induksi elektromagnetik yang disertai dengan pembahasan dan tips untuk mengerjakan soal. Soal latihan ini saya tulis menjadi 2 bagian dan ini adalah soal dan pembahasan induksi elektromagnetik bagian 1, selamat menikmati.

Soal nomor 1

Sebuah bidang limas dengan, yang ukuran rusuk seperti tampak pada gambar berikut. Diletakkan dalam suatu medan magnet homogen.

Besar induksi magnetik 0,25 T dan berarah ke sumbu Y+. Fluks magnetik melalui sisi PQRS adalah ....
A. 0,10 Wb
B. 0,12 Wb
C. 0,15 Wb
D. 0,50 Wb
E. 0,60 Wb
Kunci jawaban: "B"

pembahasan soal nomor 1:

Berdasarkan soal dapat diketahui
B = 0,25 T
A = 1,6 x 0,5 = 0,8 m²
Untuk mempermudah mengerjakan perhatikan gambar berikut

Berdasarkan gambar di atas, kita dapat mengetahui bahwa sudut yang dibentuk oleh medan magnet dengan garis normal sebesar α, dengan nilai cos α = 0,3/0,5 = 0,6. Sehingga secara matematis kita dapat menuliskan besar fluks magnetiknya sebesar
Φ = B . A . cos α
Φ = 0,25 . 0,8 . 0,6
Φ = 0,12 Wb

Soal nomor 2

perhatikan gambar berikut!

Suatu batang logam netral bergerak dengan kecepatan v ke kiri melewati daerah bermedan magnetik seragam B dengan arah keluar bidang kertas. Gambar yang paling tepat melukiskan distribusi muatan pada permukaan batang logam adalah

Kunci jawaban: "D"

pembahasan soal nomor 2:

Berlaku kaidah tangan kanan dengan aturan
Ibu jari sebagai arah kecepatan “v”
Jari telunjuk sebagai arah medan magnet “B”
Jari tengah sebagai arah arus listrik “i” Sehingga pada batang logam akan mengalir arus dari bawah ke atas, maka bagian bawah batang potensialnya lebih tinggi (+) dan bagian atas logam potensialnya lebih rendah (-)

Soal nomor 3

Sebuah pesawat terbang kecil dengan panjang sayap 10 m, terbang secara mendatar ke arah utara pada kelajuan 60 m/s dalam suatu daerah dengan medan magnetik bumi 50 μT berarah 60⁰ ke bawah terhadap arah mendatar (tanah). Besar GGL induksi antara ujung-ujung sayap adalah ....
A. 50 mV
B. 44 mV
C. 37 mV
D. 31 mV
E. 26 mV
Kunci jawaban: "E"

pembahasan soal nomor 3:

Berdasarkan soal dapat diketahui
l = 10 m
v = 60 m/s
B = 50 μT = 50 x 10^-6 T
θ = 60⁰
ε ... ?
untuk menyelesaikan soal di atas kita dapat menggunakan persamaan
ε = B l v sin θ
ε = 50 x 10^-6 . 10 . 60 . sin 60⁰
ε = 3 x 10^-2 . 0,87
ε = 2,61 x 10^-2 V
ε = 0,26 mV

Soal nomor 4

Perhatikan hal-hal berikut    
1) Menjaga suatu arus stabil pada kumparan lain yang posisinya tetap dengan kumparan A
2) Memutuskan arus dalam kumparan lainnya yang posisinya tetap di dekat kumparan A
3) Dengan cepat menggerakkan sebuah magnet ke dalam kumparan A
4) Dengan cepat menggerakkan sebuah magnet ke dalam dan keluar kumparan A
Saat terjadi secara terpisah, yang dapat menghasilkan GGL induksi pada kumparan A dengan posisi tetap ditunjukkan oleh nomor ....
A. 1)
B. 3)
C. 1) dan 3)
D. 2), 3), dan 4)
E. 1), 2), 3) dan 4)
Kunci jawaban: "D"

pembahasan soal nomor 4:

Secara proses timbulnya GGL induksi dapat digambarkan sebagai berikut
Perubahan medan magnet → perubahan fluks magnet → GGL Induksi
Perubahan medan magnet dapat terjadi dengan dua cara

1. Menggerakkan kumparan di sekitar magnet atau sebaliknya (ada kecepatan)
2. Mengubah besarnya arus listrik (bisa menggunakan arus AC atau memutus hubungkan dengan sumber arus)

Berdasarkan penjelasan di atas, maka yang dapat menghasilkan GGL induksi pada kumparan A adalah pernyataan nomor 2), 3) dan 4)

Soal nomor 5

Pada gambar berikut, kumparan 1 sedang digerakkan menuju kumparan 2.

Perhatikan pernyataan-pernyataan berikut.
1) Kelajuan kumparan 1 ditingkatkan
2) Banyak lilitan kumparan 1 ditingkatkan
3) Baterai yang dihubungkan ke kumparan 1 diganti dengan baterai yang GGL-nya lebih tinggi
4) Hambatan ditambah

Perubahan yang akan meningkatkan arus induksi dalam kumparan 2 ditunjukkan oleh pernyataan nomor....
A. 4)
B. 1) dan 4)
C. 2) dan 3)
D. 1), 2), dan 3)
E. 1), 2), 3), dan 4)
Kunci jawaban: "D"

pembahasan soal nomor 5:

Proses timbulnya arus listrik induksi dapat digambarkan sebagai berikut
Perubahan medan magnet → perubahan fluks magnet → GGL Induksi → arus induksi
Peningkatan arus induksi dapat terjadi jika GGL induksinya juga meningkat, sesuai dengan persamaan
ε = NBAω
sehingga GGL induksi sebanding dengan
N = jumlah lilitan
B = medan magnet
A = Luas penampang
ω = kecepatan sudut

maka untuk meningkatkan arus induksi (meningkatkan GGL induksi) sesuai dengan pernyataan 1), 2), dan 3)

Soal nomor 6

Suatu medan magnetik seragam B yang tegak lurus bidang kertas melewati loop, seperti ditunjukkan gambar di samping. Medan magnetik berada dalam suatu jari-jari a dengan a < b dan berubah pada laju tetap. jika GGL induksi dalam loop kawat jari-jari b adalah ε, GGL induksi dalam loop kawat jari-jari 2b adalah ....

A. Nol
B. ε/2
C. ε
D. 2ε
E. 4ε
Kunci jawaban: "E"

pembahasan soal nomor 6:

Berdasarkan soal dapat diketahui
r₁ = b
r₂ = 2b
ε₁ = ε
ε₂ ... ?
berdasarkan persamaan
ε = NBAω
kita dapat mengetahui bahwa GGL induksi sebanding dengan luas penampang, sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut

Soal nomor 7

Dua kumparan P dan Q dililitkan pada suatu inti besi lunak seperti ditunjukkan pada gambar. sakelar K mula-mula terbuka dan kemudian tertutup

Pernyataan yang benar mengenai rangkaian dengan kumparan Q setelah sakelar K ditutup adalah ....
A. Arus akan mengalir sesaat dari X ke Y melalui G
B. Arus akan mengalir sesaat dari Y ke X melalui G
C. Arus tetap akan mengalir sesaat dari X ke Y melalui G
D. Arus tetap akan mengalir sesaat dari Y ke X melalui G
E. Tidak akan ada arus mengalir di G
Kunci jawaban: "B"

pembahasan soal nomor 7:

Ketika sakelar K ditutup, maka arah arus dan induksi yang terjadi dapat digambarkan sebagai berikut

Untuk menentukan arah fluks (utama dan induksi) dan arah arus induksi dapat menggunakan kaidah tangan kanan, dimana

1. 4 jari melingkar sebagai arah arus
2. Ibu jari menunjukkan arah fluks magnetnya

Sehingga arus akan mengalir pada galvanometer, tapi ingat fluks utama hanya akan muncul jika ada perubahan arus listrik (ketika sakelar ditutup) jika kemudian sakelar dibiarkan tertutup maka tidak ada arus fluks utama yang muncul sehingga tidak ada fluks induksi dan arus listrik induksi. oleh sebab itu arus induksi hanya muncul sesaat saja.

Soal nomor 8

Sebuah solenoide dengan 200 lilitan dan luas penampang 0,7 cm² memiliki medan magnetik 0,80 T sepanjang porosnya. Jika medan magnetik dikurung dalam solenoide dan berubah pada laju 0,30 T/s. besar beda potensial dalam solenoida akan menjadi adalah ....
A. 0,18 V
B. 0,24 V
C. 0,48 V
D. 4,8 V
E. 7,2 V
Kunci jawaban: "D"

pembahasan soal nomor 8:

Berdasarkan soal dapat diketahui
N = 200 lilitan
A = 0,7 cm² = 7 x 10-5 m²
dB/dt = 0,30 T/s
ε ... ?

Soal nomor 9

Sebuah loop bidang terdiri atas empat lilitan kawat, masing-masing luasnya 300 cm2. Diarahkan tegak lurus suatu daerah medan magnetik yang besarnya bertambah secara tetap dari 10 mT menjadi 25 mT dalam waktu 5 ms. Arus induksi yang dibangkitkan dalam kumparan sebesar 72 mA, jika hambatan kumparan adalah ....
A. 5 Ω
B. 7,5 Ω
C. 10 Ω
D. 12,5 Ω
E. 15 Ω
Kunci jawaban: "A"

pembahasan soal nomor 9:

Berdasarkan soal dapat diketahui
A = 300 cm² = 3 x 10^-2 m²
N = 4
ΔB = 25 – 10
ΔB = 15 mT = 15 x 10^-3 T
Δt = 5 ms = 5 x 10^-3 s
I = 72 mA = 72 x 10^-3 A
R ... ?
Menentukan GGL Induksi
ε = NA ΔB/Δt
ε = 4 . 3 x 10^-2 (15 x 10^-3 / 5 x 10^-3)
ε = 36 x 10^-2 V
Menentukan nilai hambatan
R = ε/I
R = 36 x 10^-2 / 72 x 10^-3
R = 5 Ω

Soal nomor 10

Sebuah kawat melingkar dengan hambatan 9 Ω diletakkan dalam fluks magnetik yang berubah terhadap waktu, dinyatakan dengan Φ = (3t – 5)² . arus yang mengalir dalam kawat pada t = 4 s adalah ....
A. 4,7 A
B. 8 A
C. 18 A
D. 30 A
E. 42 A
Kunci jawaban: "A"

pembahasan soal nomor 10:

Berdasarkan soal dapat diketahui
N = 1
R = 9 Ω
Φ = (3t – 5)²
t = 4 s
I ... ?
Menentukan GGL Induksi

Menentukan arus induksi
R = ε/I
R = 42/9
R = 4,7 Ω

Soal nomor 11

Sebuah kumparan mempunyai induktansi 700 mH. besara GGL induksi yang dibangkitkan dalam kumparan itu jika ada perubahan arus listrik dari 300 mA menjadi 60 mA dalam waktu 0,02 sekon secara beraturan adalah ....
A. 2,8 V
B. 4,2 V
C. 4,8 V
D. 6,4 V
E. 8,4 V
Kunci jawaban: "E"

pembahasan soal nomor 11:

Berdasarkan soal dapat diketahui
L = 700 mH = 7 x 10^-1 H
Δi = 300 – 60
Δi = 240 mA = 24 x 10^-2 A
Δt = 0,02 s = 2 x 10^-2 s
ε ... ?
ε = L Δi/Δt
ε = 7 x 10^-1 (24 x 10^-2 / 2 x 10^-2)
ε = 7 x 10^-1 . 12
ε = 8,4 V

Soal nomor 12

Pada sebuah kumparan mengalir arus dengan persamaan I = sin πt. Jika koefisien induksi diri kumparan 8 H. GGL induksi dari yang terjadi dalam kumparan tersebut sesudah selang waktu 1/3 detik adalah ....
A. ¼π volt
B. 1/5π volt
C. ½π volt
D. 2π volt
E. 4π volt
Kunci jawaban: "E"

pembahasan soal nomor 12:

Berdasarkan soal dapat diketahui
I = sin πt
L = 8 H
t = 1/3 s
ε ... ?

Soal nomor 13

Sebuah generator menghasilkan GGL maksimum 12 V ketika kumparan berputar pada 750 rpm (rpm = rotasi per menit). GGL maksimum generator ketika kumparan berputar 2.250 rpm adalah ....
A. 4 V
B. 12 V
C. 18 V
D. 27 V
E. 36 V
Kunci jawaban: "E"

pembahasan soal nomor 13:

Berdasarkan soal dapat diketahui
ε₁ = 12 V
ω₁ = 750 rpm
ω₂ = 2.250 rpm
ε₂ ... ?
hubungan antara GGL induksi dengan kecepatan sudut dapat terlihat pada persamaan ini
ε = NBAω
berdasarkan persamaan di atas, kita dapat mengetahui bahwa GGL induksi sebanding dengan kecepatan sudut, sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut

Soal nomor 14

Sebuah trafo step-up mengubah tegangan 20 V menjadi 160 V. jika efisiensi trafo itu 75% dan kumparan sekundernya dihubungkan ke lampu 160 V, 60 W, kuat arus dalam kumparan primernya adalah ....
A. 8 A
B. 6 A
C. 4 A
D. 3 A
E. 2 A
Kunci jawaban: "C"

pembahasan soal nomor 14:

Berdasarkan soal kita dapat mengetahui
V_P = 20 V
V_S = 160 V
η = 75%
V_L = 160 V
P_L = 60 W
I_P ... ?
Jika kita melihat spesifikasi lampu, maka tegangan sekunder yang dikeluarkan oleh trafo sesuai untuk menyalakan lampu dengan optimal dengan kuat arus yang mengalir pada lampu adalah
P = V . I
60 = 160 . I
3/8 A = I
Arus yang mengalir pada lampu tersebut sama dengan arus sekunder yang dihasilkan oleh trafo. Sehingga kita dapat menentukan besar arus primernya dengan persamaan

Soal nomor 15

Sepuluh lampu 12 V/20 W terhubung paralel dengan kumparan sekunder suatu trafo step-down dengan kumparan primernya terhubung dengan sumber daya PLN 200 V. jika besar arus primer yang dapat diambil dari sumber daya PLN adalah 5/4 A, besar efisiensi trafo itu adalah ....
A. 30 %
B. 50 %
C. 75 %
D. 80 %
E. 90 %
Kunci jawaban: "D"

pembahasan soal nomor 15:

Berdasarkan soal kita dapat mengetahui
n = 10 buah
V_L = 12 V
P_L = 20 W
V_P = 200 V
I_P = 5/4 A
η ... ?
kita anggap bahwa semua lampu bekerja dengan optimal
Tegangan yang diterima oleh lampu sama dengan tegangan sekunder trafo yakni
V_S = 12 V
Setiap lampu akan mendapat tegangan 12 V dengan kuat arus yang mengalir di lampu adalah
P_L = V_L . I_L
20 = 12 . I_L
5/3 A = I_L
Untuk 10 buah lampu sejenis yang dirangkai paralel, besar kuat arus total dalam rangkaian adalah
I_tot = 5/3 . 10
I_tot = 50/3 A
Besar arus total ini sama dengan besar arus yang dihasilkan oleh trafo atau arus sekundernya. Efisiensi trafo dapat ditentukan dengan persamaan