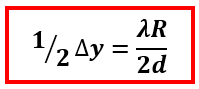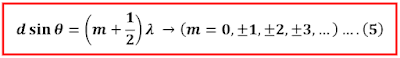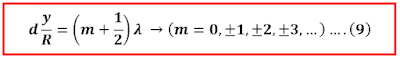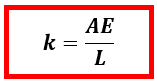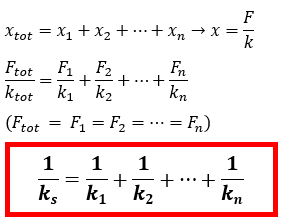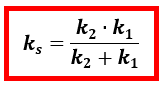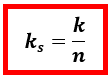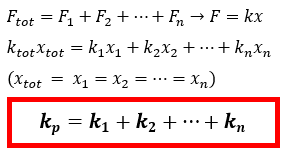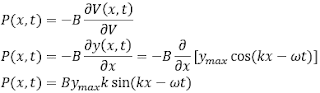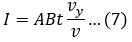Materi Fisika - Efek Doppler (video)

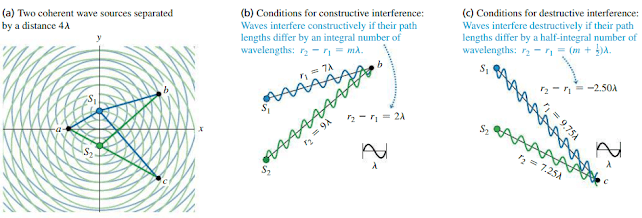
Mengenal frinji pada interferensi celah ganda (Gelombang Cahaya)

Pada interferensi celah ganda gelombang cahaya akan terbentuk pola gelap dan terang seperti yang digambarkan sebagai berikut.

Pola terang dan gelap yang terbentuk sebagai hasil dari interferensi konstruktif dan destruktif. Dimana y merupakan jarak terang atau gelap dari terang pusat (TP) sedangkan ∆y adalah jarak antar terang yang berdekatan (misalkan terang 1 ke terang 2, terang 2 ke terang 3, dst) atau jarak antar gelap yang berdekatan (misalkan gelap 1 ke gelap 2, gelap 2 ke gelap 3, dst) dan ½ ∆y adalah jarak antar terang dan gelap yang berdekatan (misalkan dari terang 1 ke gelap 1, dari gelap 1 ke terang 2, dari terang 2 ke gelap 3, dst). Seperti yang telah dijelaskan pada materi interferensi celah ganda pada gelombang cahaya, persamaan matematis berkaitan dengan pola terang adalah

d sin θ = mλ ... (m = 0, ±1, ±2, ±3, ...)

dy = mλR

y = mλR/d

persamaan matematis berkaitan dengan pola gelap adalah 

d sin θ = (m + ½)λ ... (m = 0, ±1, ±2, ±3, ...)

dy = (m + ½)λR

y = (m + ½)λR/d

Frinji sendiri merupakan jarak antar terang yang berdekatan atau jarak antar gelap yang berdekatan (∆y), sehingga lebar frinji ini adalah selisih antara jarak pola terang yang berdekatan (terang 1 dan 2, terang 3 dan 4, dst) ke pola terang pusat. Misalkan untuk mengetahui lebar frinji kita menggunakan selisih antara jarak terang kedua dan pertama terhadap terang pusat. Secara matematis dapat ditulis

∆y = y₂ – y₁ (boleh y₃ – y₂, y₄ – y₃)

∆y = m₂λR/d – m₁λR/d

∆y = 2λR/d – 1λR/d

 

Dimana :

∆y = frinji atau jarak antar terang atau gelap yang berdekatan (m)

λ = panjang gelombang (m)

R = jarak celah ke layar (m)

d = jarak antara kedua celah (m)

dari persamaan di atas, tentunya kita dapat menentukan bahwa jarak antar terang dan gelap yang berdekatan adalah setengah dari jarak antar terang atau gelap yang berdekatan.

 

konsep ini akan sangat berguna jika kita diminta untuk menentukan jarak antar terang atau dari terang ke n sampai gelap ke m. untuk lebih memahami konsep ini silahkan dibuka latihan soal tentang interferensi cahaya celah ganda.

Interferensi Cahaya pada Celah Ganda Young (Materi fisika kelas 11)

 

Gambar 1. Interferensi pada gelombang air

(sumber : University Physics with Modern Physics)

Interferensi gelombang dapat terjadi ketika gelombang di hasilkan dari dua sumber yang koheren (kedua gelombang selalu memiliki beda fase yang tetap) seperti yang terlihat pada gelombang air di atas. Interferensi pada gelombang air memang mudah dilihat akan tetapi interferensi pada gelombang cahaya susah untuk dilihat, hal ini dikarenakan cahaya yang merambat pada medium yang sama tidak dapat dilihat.

Sekitar tahun 1800 seorang ilmuwan asal inggris Thomas Young mengawali eksperimen untuk meneliti interferensi pada cahaya dengan melakukan percobaan. Skema percobaan yang dilakukan oleh Young digambarkan seperti berikut

Gambar 2. Skema percobaan interferensi cahaya celah ganda Thomas Young

(sumber : University Physics with Modern Physics)

Pada gambar 2a, terlihat sebuah sumber cahaya monokromatis ditembakkan melalui celah sempit (S_o) dengan lebar sekitar 1 μm,. Namun, cahaya yang keluar dari celah ini tidak cocok untuk digunakan dalam percobaan Inteferensi karena masih belum koheren. Oleh karena itu, oleh Young cahaya yang keluar dari celah pertama di teruskan ke dua celah selanjutnya (S₁ dan S₂) yang memiliki lebar sekitar 1 μm dan berjarak sepersepuluh atau seperseratus μm. Muka gelombang yang keluar dari celah pertama berbentuk Cylindrical kemudian menyebar hingga masuk ke celah ganda S₁ dan S₂, gelombang cahaya yang masuk ke kedua celah ini memiliki fase yang sama karena menempuh jarak yang sama dari celah pertama. Gelombang cahaya yang keluar dari celah ganda juga akan tetap sefase, sehingga celah ganda ini dapat disebut sebagai sumber cahaya yang koheren sehingga cocok digunakan dalam percobaan interferensi gelombang cahaya.

Untuk memvisualisasikan hasil interferensinya, gelombang cahaya yang keluar dari celah ganda kemudian ditangkap oleh layar sehingga terbentuk pola gelap terang pada layar seperti yang terlihat pada gambar paling kanan. Perhatikan gambar 2b yakni bentuk geometri dari interferensi cahaya yang digunakan untuk menyederhanakan dalam melakukan analisis interferensi cahaya pada titik P berkas cahaya yang berkumpul akan lebih terang hal ini menandakan terjadinya interferensi konstruktif dan di daerah sebelahnya terlihat lebih redup, hal ini menandakan terjadinya interferensi destruktif.

kita asumsikan bahwa jarak R (di beberapa buku kadang jarak celah ke layar diberi simbol “L”) dari celah ke layar jauh lebih besar daripada jarak antara kedua celah d sehingga berkas sinar-sinar yang keluar sangat mendekati sejajar (2c), hasil seperti biasanya terjadi pada percobaan dengan cahaya, jarak antar celah yang berkisar pada beberapa milimeter dibandingkan dengan jarak celah ke layar yang berkisar beberapa meter atau lebih, sehingga perbedaan panjang lintasan berkas sinar sesuai dengan persamaan 

r₂ – r₁ = d sin θ ... (1)

dimana θ merupakan sudut antara berkas sinar yang keluar dari celah dengan jarak celah ke layar (gambar 2c).

Interferensi konstruktif dan destruktif pada celah ganda

Sebelum masuk ke penjelasan interferensi konstruktif dan destruktif pada celah ganda, mari kita sejenak mengingat kembali bagaimana proses terjadinya interferensi konstruktif maupun destruktif pada gelombang. Perhatikan gambar berikut.

Gambar 3. Interferensi pada gelombang bunyi

(sumber : University Physics with Modern Physics)

Gambar 3 menunjukkan dua buah sumber gelombang S₁ dan S₂ memancarkan gelombang dengan amplitudo dan panjang gelombang (λ) yang sama, serta  fase yang konstan. misalkan kita meninjau sebuah titik a yang berada pada sumbu x dengan jarak yang sama dari kedua sumber gelombang (gambar 3a). Jika gelombang yang dihasilkan oleh kedua sumbernya memiliki amplitudo, panjang gelombang dan fase yang sama ketika gelombang meninggalkan kedua sumber adalah sefase, maka gelombang tersebut akan tiba di titik a dalam waktu yang sama dan tetap sefase. Sehingga amplitudo total di titik a akan menjadi dua kali amplitudo awalnya karena terjadi interferensi dari kedua gelombang tersebut. Hal tersebut berlaku juga untuk semua area. 

Sekarang kita perhatikan gambar 3b, terlihat bahwa jarak dari sumber ke dua (S₂) ke titik b lebih panjang 2λ dari pada jarak dari sumber kedua (S2) ke titik b. Hal ini menyebabkan sebuah puncak dari sumber pertama akan tiba di titik b dua kali lebih awal dari pada puncak dari sumber kedua yang memancar bersamaan dari sumber satu dan sumber dua. Ketika dua  puncak gelombang tiba bersamaan pada suatu titik (disebut sefase) maka amplitudo pada titik tersebut akan menjadi dua kali semula sebagai akibat dari interferensi dari kedua gelombang yang datang. Interferensi yang terjadi ketika kedua amplitudo ini saling menguatkan disebut dengan interferensi konstruktif. Misalkan jarak dari sumber pertama ke titik b disebut dengan r1 dan jarak dari sumber kedua ke titik b disebut dengan r2 maka agar terjadi interferensi konstruktif selisih jarak kedua sumber ini harus kelipatan bilangan bulat dari panjang gelombangnya (λ). Secara matematis hubungan ini dapat ditulis

r₂ – r₁ = mλ → ( m = 0, ± 1, ± 2, ±3, ... ) ... (2)

Agak sedikit berbeda jika kita melihat gambar 3c, selisih dari jarak sumber pertama ke titik c (r₁) dengan jarak dari sumber kedua ke titik c (r₂) adalah -2,50 λ, yang mana merupakan kelipatan setengah dari panjang gelombangnya. Ketika sebuah puncak gelombang (amplitudo positif) dari sumber 1 tiba di titik c, pada saat yang bersama dari sumber ke dua yang datang adalah lembah gelombang (amplitudo negatif), sehingga terjadi interferensi dari puncak dan lembah gelombang yang mengakibatkan keduanya saling melemahkan dan amplitudo di titik c sama dengan nol. Interferensi yang terjadi ketika kedua amplitudo saling melemahkan disebut dengan interferensi destruktif. Dengan kata lain interferensi destruktif akan terjadi jika selisih jarak kedua sumber ke suatu titik harus kelipatan dari setengah panjang gelombangnya (λ). secara matematis dapat ditulis

r₂ – r₁ = (m + ½) λ → ( m = 0, ± 1, ± 2, ±3, ... ) ... (3)

Interferensi konstruktif dan destruktif juga terjadi pada gelombang cahaya sehingga terjadi pola pita gelap terang pada layar seperti ditunjukkan gambar berikut.

Gambar 4. Pola gelap terang percobaan interferensi celah ganda Young yang tertangkap pada layar 

(sumber : University Physics with Modern Physics)

Pola terang menandakan terjadinya interferensi konstruktif pada titik tersebut, sedangkan pola gelap menandakan terjadinya interferensi destruktif pada titik tersebut. Dengan mensubstitusikan persamaan (1) ke persamaan (2) kita akan mendapatkan persamaan saat terjadi pita terang (interferensi konstruktif) sebagai berikut.

Sedangkan jika kita mensubstitusikan persamaan (1) ke persamaan (3), kita akan mendapatkan persamaan saat terjadi pita gelap (interferensi destruktif) sebagai berikut

perhatikan kembali gambar 2a dan gambar 4, terdapat persamaan bahwa bagian tengah dari pola tersebut terlihat paling terang, pola ini kita sebut sebagai terang pusat jarak dari pita terang atau gelap ke terang pusat adalah y (gambar 2b). berdasarkan gambar 2b kita dapat menuliskan bahwa

tan θ = y/R ... (6)

Karena jarak pola pita ke terang pusat (y) jauh lebih kecil daripada jarak dari celah ke layar (R) maka sudut θ yang terbentuk sangat kecil, sehingga nilai tan θ ≈ sin θ, sehingga persamaan (6) dapat kita tulis

sin θ = y/R ... (7)

Dengan mensubstitusikan persamaan (7) ke persamaan (4) dan (5) kita dapatkan persamaan baru yakni.

untuk pola pita terang, dan

untuk pola pita gelap.

persamaan-persamaan di atas adalah untuk menentukan jarak dari pita terang atau gelap ke terang pusat, bagaimana jika yang ditanyakan di soal adalah jarak antar pita terang, jarak antar pita gelap, atau jarak pita ke n sampai ke m? untuk itu silahkan di baca konsep tambahan tentang materi ini yakni terkait dengan frinji pada interferensi celah ganda (gelombang cahaya)

Demikian uraian singkat tentang interferensi gelombang cahaya, semoga dapat membantu para pembaca dalam memahami materi ini. Untuk lebih memahami materi ini silahkan dilihat Latihan Soal Interferensi Cahaya Celah Ganda

Hukum Hooke | Materi fisika kelas 11

Sebuah pegas ketika diberikan gaya (ditarik atau ditekan) akan kembali ke keadaan awal sesaat setelah gaya tersebut dihilangkan, hal yang sama juga berlaku untuk benda – benda yang bersifat elastis dan keadaan ini berlaku selama masih pada daerah elastis. Berdasarkan fenomena ini pada tahun 1976, seorang fisikawan bernama Robert Hooke mengemukakan hukum Hooke yang menyatakan bahwa “besarnya gaya yang diperlukan untuk meregangkan atau merapatkan sebuah pegas (gaya pegas) sama besar dengan besarnya gaya yang digunakan untuk meregangkan atau merapatkan pegas tersebut sejaub x”. Secara matematis hukum Hooke dapat ditulis

Keterangan :
F_p = gaya pegas (N)
k = Konstanta pegas (N/m)
x = perubahan panjang pegas (m)

konstanta pegas merupakan suatu nilai yang bergantung dari jenis pegas yang digunakan, konstanta pegas ini berbanding terbalik dengan perubahan panjang pegas secara matematis dapat dijelaskan bahwa semakin besar konstanta pegas berbanding terbalik dengan perubahan panjang pegas. Hal ini juga mengandung makna bahwa semakin besar konstanta pegas maka benda semakin susah untuk berubah panjangnya atau dibutuhkan gaya yang lebih besar ketika ingin mengubah panjang pegas atau dapat pula dikatakan bahwa pegas tersebut semakin bersifat tidak elastis.
Tanda negatif menunjukkan bahwa gaya pegas arahnya selalu berlawanan dengan arah perpindahannya dari titik kesetimbangan, gaya pegas juga berfungsi untuk memulihkan panjang pegas kembali ke bentuk semula, oleh karena itu gaya pegas sering juga disebut dengan gaya pemulih.
Penting
Beberapa buku menuliskan rumus di atas tanpa tanda negatif (F = kΔx), hal ini dikarenakan gaya yang dimaksud pada persamaan tersebut bukan gaya pegas akan tetapi gaya luar yang dikerjakan pada pegas tersebut. Antara gaya pegas dan gaya luar yang dikerjakan ini memang besarnya sama akan tetapi arahnya berlawanan jadi jangan sampai bingung ketika melihat kedua rumus tersebut.

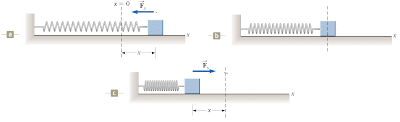
Gambar 6. Ilustrasi gaya pegas atau gaya pemulih
(sumber: Principle of Physics)

Perhatikan sebuah benda yang terhubung dengan sebuah pegas dengan salah satu ujungnya menempel di tembok, ketika balok bergerak ke kanan (x < 0) dan menarik pegas (gambar 6a) sehingga pegas menjadi lebih panjang maka arah gaya pegas akan ke kiri. Ketika balok berada pada titik kesetimbangan (gambar 6b) gaya pegas bernilai nol (x = 0), dan ketika balok bergerak ke kiri (x < 0) menekan pegas (gambar 6c) sehingga pegas menjadi lebih pendek maka gaya pegas memiliki arah ke kanan. Sehingga dari hasil mengamati gambar tersebut kita mengetahui bahwa gaya pegas berfungsi untuk mengembalikan pegas ke posisi awalnya atau posisi kesetimbangan. Hubungan antara gaya pegas dan perubahan panjang dapat pula dilihat dari grafik di bawah ini.

Gambar 7. (a) grafik hubungan antara gaya pegas dengan perubahan panjang pegas, (b) grafik hubungan antara gaya F dengan perubahan panjang pegas, (s) grafik hubungan antara gaya F dengan perubahan panjang pegas untuk beberapa pegas

Perhatikan gambar di atas, gambar 7a menunjukkan hubungan antara gaya pegas dengan perubahan panjang pegas, ketika perubahan panjang pegas bernilai negatif (x < 0 ) maka gaya pegas bernilai positif (F_p > 0) sedangkan ketika perubahan panjang pegas bernilai positif (x > 0) maka gaya pegas bernilai negatif (F_p < 0), nilai perubahan panjang pegas berlawanan dengan nilai gaya pegas hal ini sesuai dengan persamaan di atas dengan tanda minus (-). Gambar 7b sedikit berbeda dengan gambar 7a yakni terletak gaya yang digambarkan, pada grafik 7a gaya yang digambarkan dalam grafik merupakan gaya pegas (gaya pemulih) sedangkan pada grafik 7b gaya yang digambarkan dalam grafik merupakan gaya yang dikerjakan pada pegas yang sesuai dengan persamaan F = kx (tanpa tanda minus) sehingga terlihat bahwa gaya sebanding dengan perubahan panjang pegas, semakin besar gaya yang bekerja maka semakin besar pula perubahan panjang pegasnya. Jika kita analisis lebih lanjut grafik pada gambar 7b merupakan grafik berbentuk garis lurus (linier) yang mana secara matematis memiliki persamaan umum y = mx dimana m merupakan gradien dari grafik tersebut, apabila kita hubungkan antara persamaan garis lurus ini dengan persamaan hukum hooke maka
y = mx → F = kx
kedua persamaan di atas menunjukkan adanya kesesuaian dimana gaya F dianalogikan sebagai sumbu y, perubahan panjang pegas x dianalogikan sebagai sumbu x dan konstanta pegas k dianalogikan sebagai gradien grafik m. Grafik 7c menunjukkan grafik hubungan antara gaya yang bekerja dengan perubahan panjang untuk empat buah pegas, terlihat bahwa perbedaan dari semua grafik tersebut terletak pada kemiringannya (atau gradien), sehingga dengan menggunakan analisis gradien seperti di atas kita dapat mengatakan bahwa semakin curam grafiknya (gradiennya semakin besar) maka nilai konstanta pegasnya juga semakin besar yang artinya pegas tersebut semakin tidak elastis, begitu pula sebaliknya semakin landai grafiknya (gradien semakin kecil) maka nilai konstanta pegasnya semakin kecil yang artinya pegas tersebut semakin bersifat elastis. Jadi jika diurutkan berdasarkan nilai konstanta pegasnya dari terbesar ke terkecil maka k₁ > k₂ > k₃ > k₄.

Hubungan antara hukum Hooke dengan Modulus Young

Pada dasarnya baik hukum Hooke dan modulus Young sama-sama berkaitan dengan sifat elastisitas benda, tetapan pegas k berlaku untuk benda – benda elastis yang masih di daerah elastisnya (perhatikan kembali grafik hubungan antara tegangan dan regangan). persamaan hukum Hooke dan persamaan modulus Young memiliki hubungan yang saling berkaitan, jika kita telaah kembali persamaan pada modulus Young dapat kita tulis

Berdasarkan kedua persamaan di atas, maka kita dapat menuliskan persamaan untuk konstanta pegas adalah sebagai berikut

Keterangan :
k = konstanta pegas (N/m)
L = panjang benda (m)
E = Modulus Young (N/m²)
A = luas penampang (m²)
(luas penampang umumnya A = πr² , dimana r adalah jari-jari)

Hukum Hooke pada susunan pegas

Susunan pegas seri

Susunan pegas seri tampak seperti di atas dimana dua buah pegas yang masing-masing memiliki konstanta pegas k₁ dan k₂ disusun secara memanjang dengan satu sisinya saling bartauan (gambar kiri) memiliki konstanta yang identik dengan sebuah pegas dengan konstanta pegas sebesar ks (nilai ini disebut dengan konstanta pengganti), karakteristik dari pegas yang dirangkai secara seri adalah

1. Gaya total yang bekerja pada sistem sama dengan Gaya yang bekerja pada masing – masing pegas
F_tot = F₁ = F₂ = ... = F_n
2. Pertambahan panjang total sistem pegas adalah hasil penjumlahan pertambahan panjang masing – masing pegas
x_tot = x₁ + x₂ + ... + x_n
3. Konstanta pengganti susunan seri pegas (k_s) dapat ditentukan dengan cara

khusus dua pegas identik yang dirangkai seri untuk menentukan konstanta penggantinya, persamaan di atas dapat ditulis

khusus untuk "n" buah pegas identik dirangkai seri, dalam menentukan konstanta penggantinya persamaan di atas dapat ditulis

Dimana “n” adalah jumlah pegas yang dirangkai seri

Susunan pegas paralel

Susunan pegas paralel tampak seperti di atas dimana dua buah pegas yang masing-masing memiliki konstanta pegas k₁ dan k₂ disusun secara sejajar dengan kedua sisinya saling bartauan (gambar kiri) memiliki konstanta yang identik dengan sebuah pegas dengan konstanta pegas sebesar kp (nilai ini disebut dengan konstanta pengganti), karakteristik dari pegas yang dirangkai secara paralel adalah

1. gaya total yang bekerja pada sistem merupakan hasil penjumlahan dari gaya yang bekerja pada masing – masing pegas
F_tot = F₁ + F₂ + ... + F_n
2. pertambahan panjang pegas total sistem sama dengan pertambahan panjang masing – masing pegas
x_tot = x₁ = x₂ = ... = x_n
3. Konstanta pengganti susunan paralel pegas (k_p) dapat ditentukan dengan cara

Khusus untuk "n" buah pegas identik disusun paralel maka untuk menentukan konstanta pegas penggantinya persamaan di atas dapat ditulis

Dengan “n” sama dengan jumlah pegas yang disusun paralel

Penting

Perhatikan kembali karakteristik antara susunan pegas secara seri dan paralel ternyata memiliki karakteristik yang saling berlawanan, jika pada susunan pegas seri gaya totalnya sama dengan gaya pada masing – masing pegas, maka pada susunan pegas paralel pertambahan panjang pegas totalnya yang sama dengan pertambahan panjang pada masing – masing pegas. Untuk lebih memahami materi ini silahkan dilihat latihan soal tentang elastisitas

Elastisitas | Materi Fisika Kelas 11

ketika kita menarik karet atau melihat pegas yang ditekan, keduanya akan kembali ke bentuk semula ketika tarikan pada karet dilepaskan atau tekanan pada pegas dilepaskan. Kemampuan suatu benda untuk kembali ke bentuk awalnya segera setelah gaya luar yang diberikan dihilangkan disebut dengan elastisitas atau sifat elastis bendanya disebut dengan benda elastis. Semakin elastis suatu benda maka kecepatan benda tersebut kembali ke bentuk semula akan semakin cepat, akan tetapi pada kondisi tertentu benda – benda tersebut tidak mampu kembali ke bentuknya meskipun gaya luar yang dikerjakan sudah dihilangkan.

Berbeda dengan pada karet atau pegas, jika kita memberikan gaya kepada plastisin, maka plastisin tidak dapat segera kembali ke bentuk semula. Benda – benda yang seperti ini disebut dengan benda tidak elastis atau benda plastis. Baik benda elastis maupun benda plastis sama – sama memiliki fungsi dan kegunaan tersendiri, Pada kesempatan kali ini kita akan membahas tentang elastisitas suatu benda, faktor – faktor yang mempengaruhinya, kapan benda tersebut tidak dapat kembali ke bentuk semula (tidak elastis lagi). Untuk itu silahkan melanjutkan pembahasan singkat di bawah ini.

Gerak Parabola | Materi Fisika kelas 10

Lintasan kembang api pada jembatan yang berbentuk parabola

Gerak parabola merupakan gerak benda dengan lintasan yang berbentuk parabola, gerak parabola ini termasuk dalam gerak benda pada dua dimensi yang merupakan perpaduan antara gerak lurus beraturan (GLB) dengan gerak lurus berubah beraturan (GLBB). Salah satu contoh gerak parabola dapat dilihat seperti pada gambar di atas, gerak kembang api yang memancar dari atas sebuah jembatan membentuk sebuah lengkungan yang berbentuk parabola. untuk mengetahui lebih lanjut terkait dengan gerak parabola, ikuti penjelasan di bawah ini

Efek Doppler pada gelombang bunyi | Fisika Kelas 11

Mobil ambulans yang melaju dengan membunyikan sirine

(sumber : University Physics with Modern Physics)

Gelombang bunyi pada dawai dan pipa organa | Fisika kelas 11

Dua orang bermain musik (a) pemain gitar. (b) pemain terompet

(sumber : Principle of Physics)

Alat musik merupakan salah satu instrumen penghasil bunyi yang banyak digunakan dan disukai oleh orang – orang karena dapat menghasilkan nada – nada yang enak di dengar. Gambar di atas menunjukkan dua orang yang bermain alat musik gambar (a) seseorang bermain gitar sedangkan gambar (b) seseorang bermain terompet. Kedua jenis alat musik ini berbeda cara memainkannya jika gitar dengan cara di petik, terompet dengan cara ditiup, bagaimana bisa senar gitar (dawai) kolom udara pada terompet dapat menghasilkan bunyi? oleh karena itu pada kesempatan kali ini kita akan membahas materi tentang gelombang bunyi pada dawai dan pipa organa. Selamat menikmati

Intensitas Bunyi dan Taraf Intensitas Bunyi | Fisika kelas 11

Orang mendengarkan musik dari gadget atau smartphone menggunakan headset

(sumber : physics university)

Banyak orang suka mendengarkan musik melalui gagdet atau smartphone mereka menggunakan headset maupun secara langsung, ketika mendengarkan musik tentunya mereka akan menyesuaikan volumenya tidak terlalu pelan atau terlalu kencang karena ketika musik di dengarkan terlalu kencang akan menyakit telinga si pendengar. Pada saat mengubah volumenya tersebut pada dasarnya mengubah salah satu karakteristik dari gelombang bunyi yakni intensitas gelombang bunyi yang di keluarkan gadget atau smartphone mereka selain itu taraf intensitas bunyi atau “tingkat kebisingan” juga akan mempengaruhi kenyamanan ketika mendengarkan musik. Oleh sebab itu pada kesempatan kali ini kita akan membahas tentang intensitas bunyi dan taraf intensitas bunyi.

Cepat Rambat Bunyi | Fisika kelas 11

(sumber : University Physics wirh Modern Physics)

Seseorang meniup sebuah terompet di siang hari ketika musim dingin, ternyata suara di tengah cuaca yang dingin di atas pegunungan bersalju terdengar lebih pelan daripada suara ketika siang hari di musim panas di atas laut, hal ini dikarenakan elevasinya lebih tinggi. ketika musim dingin udara memiliki (i) tekanan, (ii) massa jenis atau kerapatan, (iii) kelembapan, (iv) suhu, (v) massa per mol yang lebih rendah.
Gelombang bunyi merupakan gelombang mekanik karena memerlukan medium untuk merambat, medium yang paling sering terjadi di sekitar kita adalah udara, oleh karena itu Karakterisik udara di atas akan mempengaruhi gelombang bunyi yang merambat melaluinya, akan tetapi gelombang bunyi juga dapat merambat pada medium zat cair dan zat padat. Selain itu, pada umumnya gelombang bunyi dikatakan sebagai gelombang longitudinal karena memiliki arah rambat yang sejajar dengan arah getar.
Secara sederhana gelombang bunyi dapat ditinjau sebagai gelombang transversal yang mana gelombang bunyi juga memiliki frekuensi, amplitudo dan panjang gelombang. Berdasarkan frekuensinya gelombang bunyi diklasifikasikan menjadi tiga jenis yakni gelombang bunyi yang memiliki frekuensi dalam rentang 20 – 20.000 Hz yang disebut audiosonik, gelombang ini yang mampu di dengar oleh manusia, selain itu gelombang yang memiliki frekuensi di bawah 20 Hz disebut dengan infrasonik dan gelombang bunyi yang memiliki frekuensi di atas 20.000 Hz disebut dengan ultrasonik.
Perubahan tekanan pada gelombang bunyi
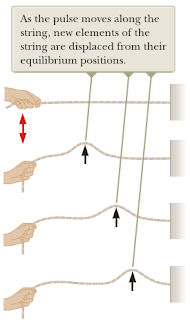
Kita sering membuktikan bentuk gelombang transversal dengan menggunakan tali yang digetarkan naik turun secara periodik, sehingga terlihat dengan jelas pergerakan untuk gerak satu gelombangnya seperti pada gambar berikut

Gambar 1. Sebuah tangan yang menggerakkan ujung tali naik turun (tanda merah) sehingga terlihat hasil gerakkan tersebut (disebut satu pulsa) berjalan di atas tali.

(sumber : physics for scientists and engineers with modern physics) 

Gambar 1 di atas menunjukkan ketika tali digerakkan satu kali naik turun maka akan terlihat sebuah pulsa yang berjalan pada tali dan jika gerakkan diteruskan maka akan terbentuk gelombang transversal (arah getar tegak lurus dengan arah rambat). Logika yang sama dapat kita gunakan untuk melihat bentuk gelombang bunyi, yakni dengan menggunakan sebuah pipa yang dapat di ubah – ubah tekanannya melalui piston yang digerakkan maju mundur untuk menghasilkan pulsa gelombang bunyi, seperti pada gambar berikut

Gambar 2. (a) proses terbentuknya rapatan ketika piston, (b) proses terbentuknya gelombang bunyi ketika piston digerakkan maju mundur.

(sumber: physics for scientists and engineers with modern physics)

Gambar 2a, menunjukkan sebuah pipa dimana disebelah kirinya terdapat piston yang dapat digerakkan maju mundur dengan cepat (gambar a), ketika piston tersebut digerakkan dengan cepat ke kanan (gambar b) maka piston tersebut akan “memukul” udara di depannya sehingga molekul – molekul udaranya menjadi lebih rapat (ditunjukkan dengan warna yang lebih gelap) dan ketika tiba – tiba piston tersebut berhenti molekul udara yang rapat tadi akan tetap bergerak maju sedangkan di bagian belakangnya susunan partikel udaranya kembali normal (gambar c). pola ketika susunan molekul udaranya menjadi lebih rapat disebut dengan “rapatan” sedangkan pola ketika susunan molekul udaranya normal disebut dengan “regangan”. Jika gerakan piston maju mundur ini dilakukan secara terus menerus dengan konstan maka akan terbentuk pola rapatan dan regangan secara bergantian seperti yang terlihat pada gambar 2b di atas dimana panjang gelombang (λ) pada gelombang bunyi merupakan jarak antar rapatan atau regangan yang terjadi, karena bunyi merupakan gelombang longitudinal maka rapatan dan regangan bergerak
jika piston berosilasi secara sinusoidal, maka kita dapat menggambarkan tiap elemen gas akan bergerak harmonik sederhana dengan persamaan posisinya dapat dituliskan

y (x,t) = ymax cos (kx – ωt) ... (1)

dimana y_max adalah posisi maksimum tiap elemen gas relatif terhadap titik kesetimbangannya atau yang sering disebut dengan perpindahan amplitudo dari gelombang. 

Tekanan yang diberikan oleh piston kepada molekul udara di dalam tabung memberikan dampak terhadap perubahan posisi molekul – molekul udara tersebut. hubungan antara perubahan tekanan P(x,t) terhadap perpindahan y(x,t) molekulau yang sering disebut dengan perpindahan amplitudo dari gelombang. Tekanan yang diberikan oleh piston kepada molekul udara di dalam tabung memberikan dampak terhadap perubahan posisi molekul – molekul udara tersebut. hubungan antara perubahan tekanan P(x,t) terhadap perpindahan y(x,t) molekulrikan dampak terhadap perubahan posisi molekul – molekul udara tersebut. hubungan antara perubahan tekanan P(x,t) terhadap perpindahan y(x,t) molekul, dapat kita analisis melalui gambar berikut

Gambar 3. Gelombang bunyi yang merambat melalui sumbu x, batas kiri dan kanan mengalami perpindahan sejauh y₁ dan y₂

(sumber : University Physics with Modern Physics)

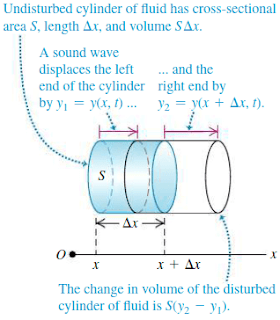
Kita dapat menganalisis hubungan antara perubahan tekanan terhadap perpindahan dengan mengambil bagian kecil dari udara (ditunjukkan dengan bentuk silinder) ketika ada gelombang bunyi ke kanan seperti yang terlihat pada gambar 3 di atas. Pada saat tidak ada bunyi, maka silinder memiliki panjang Δx dan luas permukaannya adalah S sehingga akan Volumenya V = S Δx, yang ditunjukkan dengan gambar bagian arsiran biru, saat sebuah gelombang bunyi lewat pada saat t bagian silinder yang awalnya berada di titik x akan mengalami perpindahan sebesar y₁ = y(x, t) dan bagian silinder yang awalnya berada di titik x + Δx akan mengalami perpindahan sebesar y₂ = y(x + Δx, t) yang ditunjukkan oleh garis merah. Jika y₂ > y₁ (seperti pada gambar 3) maka volume silinder akan meningkat yang disebabkan tekanannya menurun, jika y₂ < y₁ maka volume silinder akan menurun yang disebabkan tekanannya meningkat. Secara matematis perubahan volume pada silinder dapat ditulis

ΔV = S (y2 – y1) = S [y (x + Δx,t) – y(x,t)] = SΔy ... (2)

Hubungan perubahan tekanan sepanjang sumbu x dan perpindahan terhadap sumbu x molekul dapat pula digambarkan dalam grafik berikut ini

Gambar 4. Ilustrasi gelombang bunyi

(sumber : University Physics with Modern Physics)

Gambar 4a merupakan grafik hubungan antara perpindahan terhadap sumbu x, gambar 4b merupakan ilustrasi perpindahan partikel gas dalam medium dan gambar 4c merupakan grafik hubungan antara tekanan terhadap sumbu x. Berdasarkan ketiga gambar tersebut kita dapat menganalisis bahwa ketika terbentuk rapatan (Compression) gelombang perpindahan molekul bernilai minimal sedangkan tekanan yang diberikan bernilai maksimal (massa jenisnya terbesar), begitu pula sebaliknya ketika terjadi regangan (Rarefaction) gelombang perpindahan molekul bernilai maksimal sedangkan tekanan yang diberikan bernilai minimal (massa jenisnya terkecil). Hal ini terlihat jelas dari bentuk grafik yang terbentuk (grafik 4a dan grafik 4c), secara matematis hubungan antara perpindahan molekul dengan perubahan tekanan dapat ditulis.

Persamaan (3) di atas menunjukkan hubungan antara perubahan tekanan terhadap perpindahan molekul gas, dimana B merupakan modulus Bulk yakni “perbandingan antara tegangan dan regangan untuk volume (Bulk) suatu benda”, A merupakan perpindahan amplitudonya dan k merupakan bilangan gelombangnya (k = 2π/λ). berdasarkan persamaan di atas kita dapat mengetahui bahwa perpindahan amplitudo didefinisikan sebagai fungsi cosinus sedangkan tekanan didefinisikan sebagai fungsi sinus dimana perpindahan dan tekanan memiliki perbedaan sudut fase sebesar 90⁰. Kita juga dapat mengetahui hubungan antara tekanan dan perpindahan sebagai berikut.

Persamaan (4) menunjukkan tekanan maksimal atau tekanan amplitudo (P_max). Gelombang bunyi yang melewati medium dengan modulus Bulk lebih besar akan semakin susah mengalami rapatan sehingga membutuhkan tekanan yang lebih besar (tekanan sebanding dengan modulus Bulk)

Cepat rambat gelombang bunyi
Gelombang bunyi dapat merambat melalui zat cair, zat padat, maupun zat gas, cepat rambat gelombang bunyi pada masing – masing zat memiliki persamaan tersendiri sehingga. Masing – masing zat tersebut memiliki karakteristik tersendiri sehingga akan mempengaruhi cepat rambat bunyinya. Secara umum cepat rambat gelombang (transversal maupun longitudinal) dapat dirumuskan sebagai berikut

Elastisitas medium dan inersia medium inilah yang menjadi faktor penentu cepat rambat bunyi pada suatu medium karena tiap zat (cair, padat, dan gas) berbeda – beda nilainya. Berikut tabel cepat rambat gelombang bunyi pada beberapa medium

Tabel 1. Cepat Rambat Bunyi di berbagai medium

Medium	v (m/s)	Medium	v (m/s)	Medium	v (m/s)
Zat Gas Hidrogen (00C) Helium (00C) Udara (200C) Udara (00C) Oksigen (00C	1.286 972 343 331 317	Zat Cair (250C) Gliserin Air Laut Air Air Raksa Minyak Tanah Metanol Carbon Tetrakloride	1.904 1.533 1.493 1.450 1.324 1.143 926	Zat Padat Kaca Pyrex Besi Aliminium Kuningan Tembaga Emas Kaca Akrilik Timbal Karet	5.640 5.950 6.420 4.700 5.010 3.240 2.680 1960 1.600

Sumber : Physics for scientists and engineers with modern physics

Berdasarkan tabel 1 di atas, kita dapat mengetahui bahwa cepat rambat bunyi di udara pada suhu 0⁰C adalah 331 m/s sedangkan cepat rambat bunyi di udara pada suhu 20⁰C adalah 343 m/s, hal ini menunjukkan adanya pengaruh suhu terhadap cepat rambat bunyi pada suatu medium semakin tinggi suhu mediumnya maka bunyi akan merambat semakin cepat.

Cepat rambat bunyi pada zat cair

Gambar 5. Gelombang bunyi merambat pada fluida di dalam sebuah tabung (a) zat cair dalam kondisi seimbang, (b) pada saat “t” setelah piston bergerak ke kanan dengan kecepatan “v” sehingga fluida di antara piston dan titik P bergerak (piston diibaratkan gelombang bunyi yang merambat dengan kecepatan “v”)
(sumber: University Physics with Modern Physics)

Gambar 5 menunjukkan sebuah fluida dengan massa jenis ρ di dalam sebuah tabung dengan luas permukaan A, fluida dalam kondisi seimbang di bawah tekanan p pada luas permukaannya. Dalam keadaan ini panjang fluida adalah sebesar s = v t dengan v merupakan cepat rambat gelombang bunyi di fluida (gambar 5a). kita asumsikan bahwa panjang tabung sebagai sumbu x yang juga arah gelombang longitudinal ketika merambat.
Pada saat t = 0 s piston mulai bergerak dari kiri ke kanan dengan kecepatan v_y (gerakan piston ini juga menandai gelombang bunyi mulai merambat) sehingga pada zat cair akan tertekan sebagian selama beberapa saat. Pergerakan piston ini disebabkan penambahan tekanan pada piston sebesar Δp sehingga total tekanan pada bagian kiri titik P menjadi p + Δp (arah ke kanan) dan zat cair bergerak dengan kecepatan v_y selama t s sehingga mengalami perpindahan sejauh s_y = v_y . t. kita dapat menentukan besar kecepatan gelombang bunyi di dalam fluida dengan menggunakan teorema Impuls – Momentum seperti berikut
Δp = I ... (6)
Impuls (I) ditimbulkan dari gaya yang digunakan untuk menekan piston
I = F Δt = A Δp Δt = A Δp t
Perubahan tekanan dapat hubungkan dengan modulus Bulk sesuai dengan persamaan berikut ini.

Sehingga persamaan impuls di atas dapat ditulis

Sedangkan perubahan momentum yang terjadi adalah perubahan momentum elemen massa dari fluida yang bergerak dari keadaan awal (diam) hingga memiliki kecepatan v_y
Δp = m Δv = (ρV) (v_y – 0) = ρ v A t v_y ... (8)
Substitusikan persamaan (7) dan (8) ke persamaan (6) sehingga menjadi

Keterangan :
v = cepat rambat bunyi di dalam zat fluida
B = modulus Bulk Fluida
ρ = massa jenis fluida

Cepat rambat bunyi pada zat padat
Gelombang bunyi yang melewati suatu zat pada juga memiliki cepat rambat tersendiri, jika kita perhatikan kembali persamaan (5) dan (9) di atas maka kita akan mengetahui suatu pola yang sama dan dengan cara yang sama dengan menemukan cepat rambat gelombang bunyi di fluida kita dapat menuliskan persamaan matematis untuk menentukan cepat rambat gelombang bunyi pada zat padat adalah sebagai berikut.

Keterangan :
v = cepat rambat bunyi di dalam zat fluida
Y = modulus Young zat padat
μ = massa jenis linear zat padat (massa per satuan panjang)

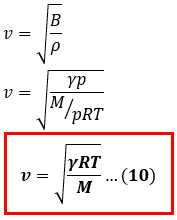
Cepat rambat bunyi pada zat gas
Sebagian besar gelombang bunyi yang terjadi di sekitar kita merambat melalui medium udara, untuk menentukan Cepat rambat bunyi di udara sedikit berbeda dengan menentukan cepat rambat bunyi di fluida maupun zat padat, perlu diketahui bahwa modulus Bulk untuk udara dipengaruhi oleh tekanan udaranya semakin besar tekanan yang diberikan untuk mengkompresikan gas maka semakin besar ketahanan (tekanan untuk menolak) dari gas tersebut sehingga modulus Bulknya semakin besar juga. Oleh karena itu modulus Bulk pada zat gas dapat ditulis dengan persamaan sebagai berikut
B = γp
Dimana B adalah modulus Bulk zat gas, γ adalah konstanta Laplace, dan P adalah tekanan udara. Konstanta Laplace sendiri merupakan karakteristik dari gas tersebut, misalkan untuk udara udara memiliki konstanta Laplace sebesar 1,4. Berikut data konstanta Laplace untuk beberapa jenis zat gas

Tabel 2. Konstanta Laplace beberapa jenis zat gas pada tekanan rendah

Jenis Gas	Gas	γ
Monoatomik     Diatomik         Polyatomik	He Ar   H2 N2 O2 CO   CO2 SO2 H2S	1,67 1,67   1,41 1,40 1,40 1,40   1,30 1,29 1,33

Sumber : University Physics with modern physics

Sedangkan massa jenis zat gas dapat ditentukan dengan persamaan
ρ = pM / RT
p adalah tekanan gas, M adalah massa atom relatif dari gas, R adalah konstanta gas ideal dan T adalah suhu gas. berdasarkan kedua persamaan di atas kita dapat menurunkan persamaan cepat rambat bunyi di gas dari persamaan (9) seperti berikut

Persamaan 10 menunjukkan bahwa cepat rambat gelombang bunyi di zat gas juga ditentukan oleh suhu dari gas tersebut (tidak hanya dari jenis zat gasnya). Semakin besar suhu dari zat gas maka semakin cepat bunyi akan merambat melaluinya, hal ini juga terlihat pada tabel 1 di atas dimana gelombang bunyi yang merambat pada udara dengan suhu 20⁰C lebih cepat daripada ketika gelombang bunyi merambat melalui udara pada suhu 0⁰C

Contoh soal dan pembahasan

Soal nomor 1

A sinusoidal sound wave moves through a medium and is described by the displacement wave function
s(x, t) = 2,00 cos (15,7x - 858t)
where s is in micrometers, x is in meters, and t is in seconds. Find (a) the amplitude, (b) the wavelength, and (c) the speed of this wave. (d) Determine the instantaneous displacement from equilibrium of the elements of the medium at the position x = 0.050 0 m at t = 3.00 ms. (e) Determine the maximum speed of the element’s oscillatory motion.
Terjemahan :
Sebuah gelombang bunyi merambat melalui sebuah medium dan perpindahannya sesuai dengan persamaan
S(x, t) = 2,00 cos (15,7 x – 858t)
Dimana s dalam mikrometer, x dalam meter dan t dalam sekon. tentukan (a) amplitudo, (b) panjang gelombang, dan (c) cepat rambat gelombang. (d) tentukan perpindahan sesaat dari titik setimbang sebuah elemen dari medium tersebut pada saat posisi x = 0,0500 m dan t = 3,00 ms. (e) tentukan kecepatan maksimum dari gerakan gelombang tersebut.

pembahasan soal nomor 1:

Berdasarkan soal dapat diketahui
Persamaan Perpindahan
S(x, t) = 2,00 cos (1,57 x – 858t)
Dari persamaan tersebut kita bisa mengetahui
A = 2 μm
k = 15,7 m^-1
ω = 858 rad/s

(a) Amplitudo gelombang
A = 2 μm
A = 2 x 10^-6 m

(b) Panjang gelombang (λ)
λ = 2π/k
λ = 2π / 15,7
λ = 2 . 3,14 / 15,7
λ = 0,4 m

(c) Cepat rambat gelombang (v)
v = ω/k
v = 858 / 15,7
v = 54,6 m/s

(d) s ... ? (x = 0,05 m, t = 3 ms = 3 x 10^-3 s)
s = 2 μm cos (1,57 (0,05) – 858 (3 x ^10-3)
s = 2 μm cos (-1,789)
s = 2 μm (-0,216)
s = - 0,432 μm

(e) persamaan kecepatan
v = ds/dt
v = d/dt (2 x 10^-6 cos (15,7 x – 858t))
v = (2 x 10^-6)(858) sin (15,7 x – 858t)
v = 1,7 x 10^-3 sin (15,7 x – 858t)
kecepatan maksimum di dapatkan ketika nilai sinusnya sama dengan 1, sehingga dari persamaan kecepatan di atas kita dapat mengetahui kecepatan maksimumnya adalah vmax = 1,7 x 10^-3 m/s

Soal nomor 2

Consider a sound wave in air that has displacement amplitude 2.20 x 10^-2 mm. Calculate the pressure amplitude for frequencies of (a) 145 Hz; (b) 15,00 Hz; (c) 1.41 x 10⁴ Hz. In each case compare the result to the pain threshold, which is 30 Pa.
Terjemahan :
Pertimbangkan gelombang bunyi yang merambat di udara memiliki perpindahan amplitudo sebesar 2,20 x 10^-2 mm. Hitunglah tekanan amplitudonya pada saat frekuensinya (a) 145 Hz; (b) 15,00 Hz; (c) 1,41 x 10s⁴ Hz. Dalam setiap kasus bandingkan hasilnya dengan tingkat ambang batas nyeri yakni sebesar 30 Pa.

pembahasan soal nomor 2:

Berdasarkan soal dapat diketahui
A = 2,20 x 10^-2 mm = 2,20 x 10^-5 m
B = 1,42 x 10⁵ (modulus Bulk udara)
v = 344 m/s (cepat rambat gelombang bunyi di udara)
kita gunakan persamaan k = 2πf/v
(a) f = 145 Hz
P_max = B A k
P_max = B A (2πf/v)
P_max = 1,42 x 10⁵ . 2,2 x 10^-5 (2 . 3,14 . 145 / 344)
P_max = 8,27 Pa
Di bawah ambang batas nyeri

(b) f = 15 Hz
P_max = B A k
P_max = B A (2πf/v)
P_max = 1,42 x 10⁵ . 2,2 x 10^-5 (2 . 3,14 . 15 / 344)
P_max = 0,86 Pa
Di bawah ambang batas nyeri

(c) f = 1,41 x 10⁴ Hz
P_max = B A k
P_max = B A (2πf/v)
P_max = 1,42 x 10⁵ . 2,2 x 10^-5 (2 . 3,14 . 1,41 x 10⁴ / 344)
P_max = 804,14 Pa
Di atas ambang batas nyeri

Soal nomor 3

Write an expression that describes the pressure variation as a function of position and time for a sinusoidal sound wave in air. Assume the speed of sound is 343 m/s, λ = 0.100 m, and ΔP_max = 0.200 Pa.
Terjemah :
Tuliskan persamaan perubahan tekanan sebagai fungsi posisi dan waktu untuk gelombang bunyi di udara. Asumsikan cepat rambat gelombang bunyi adalah 343 m/s, λ = 0,100 m , dan ΔP_max = 0,200 Pa

pembahasan soal nomor 3:

Berdasarkan soal dapat diketahui
v = 343 m/s
λ = 0,1 m
ΔP_max = 0,2 Pa
Persamaan untuk perubahan tekanan dalam fungsi posisi dan waktu adalah
ΔP (x,t) = ΔP_max sin (kx – ωt)
Menentukan bilangan gelombang “k”
k = 2π/λ
k = 2 . 3,14 / 0,1
k = 62,8 m^-1
Menentukan frekuensi sudut gelombang “ω”
ω = k v
ω = 62,8 . 343
ω = 2,15 x 10⁴ rads^-1

sehingga persamaan di atas dapat ditulis
ΔP (x,t) = 0,2 sin (62,8x – 2,14 x 10⁴t)

Soal nomor 4

An experimenter wishes to generate in air a sound wave that has a displacement amplitude of 5.50 x 10^-6 m. The pressure amplitude is to be limited to 0.840 Pa. What is the minimum wavelength the sound wave can have?
Terjemahan :
Seseorang melakukan eksperimen gelombang bunyi di udara sehingga diharapkan gelombang yang terbentuk memiliki perpindahan amplitudo sebesar 5,50 x 10^-6 m. tekanan amplitudo dibatasi sebesar 0,840 Pa. Berapa panjang gelombang minimum yang dapat kita gunakan?

pembahasan soal nomor 4:

Berdasarkan soal dapat diketahui
A = 5,50 x 10^-6 m
ΔPmax = 0,840 Pa
v = 343 m/s (cepat rambat bunyi di udara)
λ ... ?
persamaan tekanan amplitudo adalah
ΔP_max = B A k
Dengan B = v² . ρ dan k = 2π/λ
Sehingga persamaan tersebut dapat ditulis
ΔP_max = (v².ρ) A (2π/λ)
ΔP_max λ = 2π v²ρ A
0,84 λ = 2 . 3,14 . (343)² . 1,2 . 5,5 x 10^-6
0,84 λ = 4,88
λ = 5,809 m

Soal nomor 5

(a) In a liquid with density 1200 kg/m³, longitudinal waves with frequency 430 Hz are found to have wavelength 8.50 m. Calculate the bulk modulus of the liquid. (b) A metal bar with a length of 1.50 m has density 6100 kg/m³. Longitudinal sound waves take 3.60 x 10^-4 s to travel from one end of the bar to the other. What is Young’s modulus for this metal?
Terjemahan :
(a) Sebuah cairan dengan massa jenis 1200 kg/m³, ditemukan gelombang longitudinal dengan frekuensi 430 Hz memiliki panjang gelombang 8,50 m. hitunglah modulus Bulk cairan. (b) sebuah batang logam dengan panjang 1,50 m memiliki massa jenis 6100 kg/m³. Gelombang longitudinal bunyi memerlukan 3,60 x 10^-4 s untuk berjalan dari satu ujung ke yang lain pada loga,. Berapa modulus Young dari logam tersebut?

pembahasan soal nomor 5:

Berdasarkan soal dapat diketahui

(a) ρ = 1200 kg/m³
f = 430 Hz
λ = 8,50 m
modulus Bulk dapat ditentukan dengan persamaan
B = v² ρ
B = (λ f)² ρ
B = (8,5 . 430)² . 1200
B = 16,03 x 10⁹

(b) L = 1,50 m
ρ = 6100 kg/m³
t = 3,60 x 10^-4 s
Modulus Young dapat ditentukan dengan persamaan
Y = v² ρ → v = L/t
Y = (L/t)² ρ
Y = (1,5 / 3,6 x 10^-4)² . 6100
Y = 10,59 . 10¹⁰

Soal nomor 6

A submerged scuba diver hears the sound of a boat horn directly above her on the surface of the lake. At the same time, a friend on dry land 22.0 m from the boat also hears the horn (Fig. E16.7). The horn is 1.90 m above the surface of the water. What is the distance (labeled “?”) from the horn to the diver? Both air and water are at 20⁰C.

Terjemahan :
Seorang penyelam mendengar suara dari klakson kapal yang tepat di atas permukaan danau di atasnya. Pada saat bersamaan temannya yang berada di daratan yang berjarak 22,0 m dari kapal boat juga mendengar klakson suara kapal boal (liat gambar E16.7). klakson berada 1,90 m di atas permukaan air. tentukan jarak (diberi tanda “?” dari klakson ke penyelam? Keduanya baik udara dan air bersuhu 20⁰C

pembahasan soal nomor 6:

Berdasarkan soal dapat diketahui
S_kt = 22,0 m (jarak klakson ke teman)
S_ka = 1,90 m (jarak klakson ke air)
v_u = 344 m/s (cepat rambat bunyi di udara)
v_a = 1480 m/s (cepat rambat bunyi di air)
S_kp = ... ? (jarak klakson ke penyelam)
Perlu diperhatikan karena pada soal ada keterangan “pada saat yang bersamaan” hal ini menunjukkan waktu untuk gelombang bunyi merambat dari klakson ke teman di daratan dan dari klakson ke penyelam adalah sama
Tinjau teman di daratan
S_kt = v_u . t
t = S_kt / v_u ... (1)
Tinjau penyelam
Karena dari klakson ke penyelam melewati dua medium yakni udara dan air, waktu total yang dibutuhkan gelombang bunyi dari klakson ke penyelam dapat ditulis
t = t₁ + t₂
dimana :
t₁ : waktu gelombang bunyi merambat dari klakson ke air
t₂ : waktu gelombang bunyi merambat dari air ke penyelam
sehingga persamaan di atas dapat ditulis
t = S_ka / v_u + S_ap / v_a ...(2)

dari persamaan (1) dan (2) kita dapat menuliskan

Sehingga jarak total dari klakson ke penyelam adalah
S_kp = S_ka + S_ap
S_kp = 1,90 + 86,43
S_kp = 88,33 m

Soal nomor 7

At a temperature of 27.0⁰C, what is the speed of longitudinal waves in (a) hydrogen (molar mass 2.02 g/mol); (b) helium (molar mass 4.00 g/mol); (c) argon (molar mass 39.9 g/mol)? See Table 2 for values of γ.
Terjemahan :
Pada temperatur 27,0⁰C, tentukan kecepatan gelombang longitudinal di (a) hidrogen (M = 2,02 g/mol); (b) helium (M = 4,00 g/mol); (c) argon (M = 39,9 g/mol)? Lihat tabel 2 untuk menentukan nilai γ. 

pembahasan soal nomor 7:

Berdasarkan soal dapat diketahui
T = 27⁰C = 300 K
M_H2 = 2,02 g/mol
M_He = 4,00 g/mol
M_Ar = 39,9 g/mol
γ_H2 = 1,41
γ_He = 1,67
γ_Ar = 1,67
v ... ?
untuk cepat rambat gelombang bunyi di udara kita dapat menggunakan persamaan 10

Sub Materi Gelombang Bunyi

Cepat Rambat Bunyi | Intensitas dan Taraf Intensitas Bunyi | Bunyi pada Dawai dan Pipa Organa | Efek Doppler pada Gelombang Bunyi

Latihan Soal Gelombang Bunyi

PART 1 | PART 2 | PART 3