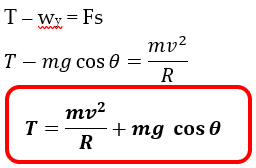Gaya Sentripetal pada Benda Terhubung Tali (Penjelasan Lengkap)

Gaya sentripetal merupakan gaya yang arahnya menuju pusat lingkaran pada benda yang bergerak melingkar, hubungannya dengan hukum Newton adalah terkait dengan gaya – gaya yang berlaku sama dengan gaya sentripetal dan hal ini bergantung pada kasus atau fenomena dalam soal. Beberapa di antaranya yaitu benda yang terhubung tali, jalan menikung, dan jalan yang melengkung. Mari kita bahas satu persatu. Nah, pada kesempatan kali ini pembahasan lengkap tentang gaya sentripetal pada benda terhubung tali. selamat menikmati

Benda terhubung tali

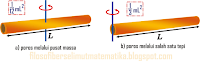
Benda yang terhubung tali dapat digerakkan secara melingkar baik melingkar vertikal dan melingkar horizontal seperti yang ditunjukkan pada gambar di bawah ini

Pada kedua gambar di atas misalkan benda bermassa m bergerak melingkar dengan kecepatan linier sebesar v sehingga gaya sentripetal yang dimiliki benda tersebut adalah

Sehingga kita dapat melakukan analisisnya sebagai berikut

Bergerak horizontal

Ketika benda bergerak melingkar secara horizontal seperti pada gambar (1) di atas, maka gaya yang bertindak sebagai gaya sentripetal adalah gaya tegang tali tersebut, secara matematis dapat ditulis
T = Fs

Persamaan di atas menunjukkan gaya tegang tali ketika benda berputar secara horizontal dimana R merupakan jari – jari lingkaran.

Bergerak vertikal

Gambar (2) menunjukkan gerakan benda terikat tali dan diputar secara vertikal, sedikit berbeda dengan sebelumnya ketika benda bergerak secara vertikal maka posisi benda mempengaruhi arah gaya yang bekerja sehingga persamaan gaya sentripetal bisa berubah bergantung pada posisi benda tersebut, perlu diingat bahwa gaya sentripetal merupakan gaya yang arahnya menuju pusat lingkaran hasil resultan gaya – gaya tersebut. Berikut akan terlihat bagaimana posisi benda akan mempengaruhi persamaan gaya sentripetalnya
Posisi A

Berdasarkan gambar di atas yang bertindak sebagai gaya sentripetal adalah gaya tegang tali, maka persamaan gaya sentripetalnya adalah

Posisi B

Berdasarkan gambar di atas, gaya sentripetal merupakan resultan dari gaya tegang tali dan gaya berat benda. Sehingga persamaan gaya sentripetalnya menjadi

Posisi C

Berdasarkan gambar di atas, gaya sentripetal merupakan resultan dari gaya tegang tali dan gaya berat benda dalam komponen sumbu y (w_y). Sehingga persamaan gaya sentripetalnya menjadi

gambar D

Berdasarkan gambar di atas, gaya sentripetal merupakan resultan dari gaya tegang tali dan gaya berat benda dalam komponen sumbu x (w_x). Sehingga persamaan gaya sentripetalnya menjadi

Posisi E

Berdasarkan gambar di atas, gaya sentripetal merupakan resultan dari gaya tegang tali dan gaya berat (arah keduanya sama). Sehingga persamaan gaya sentripetalnya menjadi

agar lebih memahami konsep gaya sentripetal pada benda terhubung tali ini secara lengkap, mari kita simak beberapa contoh soal di bawah ini yang juga disertakan pembahasan dan penjelasan lengkap.

Soal nomor 1
Sebuah bola bermassa 200 g yang diikat di ujung tali diayun dalam suatu lingkaran horizontal beradius 50 cm. Bola tersebut melakukan 150 putaran tiap menit. hitung:

1. Waktu untuk satu putaran
2. Percepatan sentripetal
3. Tegangan tali

pembahasan soal nomor 1:

Berdasarkan soal dapat diketahui
m = 200 g = 0,2 kg
R = 50 cm = 0,5 m
ω = 150 put/menit
ω =150 . 2π / 60 rad/s
ω = 5π rad/s

a. waktu untuk satu putaran
yang dimaksud dengan waktu satu putaran adalah periodenya, sehingga jika bola tersebut melakukan 150 putaran per menit atau dalam 60 s, maka
150 put = 60 s
1 put = 60/150 s
1 put = 0,4 s
Dengan kata lain periodenya adalah 0,4 s

b. percepatan sentripetal
percepatan sentripetal dapat ditentukan dengan persamaan
a_s = ω²R
a_s = (5π)² . 0,5
a_s = 25π² . 0,5
a_s = 50π² m/s²

c. tegangan tali
seperti yang telah dijelaskan di atas, untuk tali yang diputar secara horizontal gaya tegangan talinya sama dengan gaya sentripetal sehingga
T = Fs
T = m a_s
T = 0,2 . 50π²
T = 10π² N

Soal nomor 2
perhatikan gambar berikut

Sebuah benda bermassa 1 kg digantungkan pada seutas tali. Berapakah kecepatan benda di titik C jika pada titik ini T = 0 dan panjang tali 5 m?

pembahasan soal nomor 2:

Berdasarkan soal dapat diketahui
m = 1 kg
R = 5 m
θ = 30⁰
T_C = 0
Untuk menyelesaikan soal ini kita dapat menggunakan analisis benda seperti pembahasan di atas pada posisi D, sehingga persamaan matematisnya adalah

Soal nomor 3
Sebuah keping bermassa 0,500 kg diikatkan pada ujung tali yang panjangnya 1,50 m. Keping bergerak dalam lingkaran horizontal seperti yang ditunjukkan pada Gambar 6.1. Jika tali dapat menahan tegangan maksimum 50,0 N, berapakah kecepatan maksimum keping dapat bergerak sebelum tali putus? Asumsikan tali tetap horizontal selama gerakan.
Teks asli
A puck of mass 0.500 kg is attached to the end of a cord 1.50 m long. The puck moves in a horizontal circle as shown in Figure 6.1. If the cord can withstand a maximum tension of 50.0 N, what is the maximum speed at which the puck can move before the cord breaks? Assume the string remains horizontal during the motion.

Figure 6.1

pembahasan soal nomor 3:

Berdasarkan soal dapat diketahui
m = 0,5 kg
R = 1,5 m
T = 50,0 N
v_max... ?
karena benda bergerak melingkar secara horizontal maka besar tegangan talinya sama dengan besar gaya sentripetal. Jadi dapat dikatakan bahwa besar tegangan tali tersebut merupakan batas maksimal agar tali tidak putus. Kita dapat menggunakan persamaan
FS = T
mv²/R = T
v² = TR / m
v² = 50 . 1,5 / 0,5
v² = 150
v = 12,2 m/s
jadi jika kecepatannya melebihi 12,2 m/s maka gaya sentripetalnya akan melebihi 50,0 N sehingga menyebabkan tali tersebut putus.

Soal nomor 4
Sebuah bola bermassa m = 0,275 kg berayun dalam lintasan melingkar vertikal pada tali L = 0,850 m seperti pada Gambar P6.45. (a) Berapakah gaya-gaya yang bekerja pada bola di setiap titik pada lintasan? (b) Gambarlah diagram gaya untuk bola saat berada di dasar lingkaran dan saat berada di atas. (c) Jika kecepatannya 5,20 m/s di puncak lingkaran, berapakah tegangan tali di sana? (d) Jika tali putus ketika tegangannya melebihi 22,5 N, berapakah kecepatan maksimum yang dapat dimiliki bola di dasar sebelum itu terjadi? Teks Asli
A ball of mass m = 0.275 kg swings in a vertical circular path on a string L = 0.850 m long as in Figure P6.45. (a) What are the forces acting on the ball at any point on the path? (b) Draw force diagrams for the ball when it is at the bottom of the circle and when it is at the top. (c) If its speed is 5.20 m/s at the top of the circle, what is the tension in the string there? (d) If the string breaks when its tension exceeds 22.5 N, what is the maximum speed the ball can have at the bottom before that happens?

Figure P6.45

pembahasan soal nomor 4:

Berdasarkan soal dapat diketahui
m = 0,275 kg
R = 0,85 m
(a)Pada setiap titik dalam benda yang bergerak melingkar vertikal benda akan mendapatkan dua gaya yakni gaya berat (w = m g) yang arahnya ke bawah dan gaya tegang tali (T) yang arahnya menuju pusat lingkaran
(b)Gambar diagram gaya ketika benda berada di titik bawah (sama dengan posisi B pada penjelasan di atas) adalah sebagai berikut

Jadi antara gaya berat dan gaya tegang tali berlawanan arah, sedangkan diagram gaya ketika benda berada di titik atas (sama dengan posisi E pada penjelasan di atas) adalah sebagai berikut

Jadi antara gaya berat dan gaya tegang tali memiliki arah yang sama
(c) Jika ketika berada di posisi atas kecepatan benda sebesar 5,20 m/s dan dengan melihat diagram gaya pada jawaban sebelumnya, maka kita dapat menuliskan persamaan untuk gaya sentripetalnya adalah sebagai berikut

(d) jika tegangan tali maksimumnya 22,5 N pada posisi bawah, maka kecepatan maksimumnya dapat ditentukan dengan persamaan

Soal nomor 5
Sebuah benda bermassa m₁ = 4,00 kg diikat ke sebuah benda bermassa m₂ = 3,00 kg dengan Tali 1 dengan panjang l = 0,500 m. Kombinasi tersebut diayunkan dalam lintasan melingkar vertikal pada tali kedua, Tali 2, dengan panjang l = 0,500 m. Selama gerakan, kedua senar selalu segaris seperti yang ditunjukkan pada Gambar P6.44. Pada puncak geraknya, m₂ bergerak dengan kecepatan v = 4,00 m/s. (a) Berapakah tegangan tali l saat ini? (b) Berapakah tegangan tali 2 saat ini? (c) Tali mana yang akan putus lebih dulu jika kombinasi diputar lebih cepat dan lebih cepat?
Teks Asli
An object of mass m₁ = 4.00 kg is tied to an object of mass m₂ = 3.00 kg with String 1 of length l = 0.500 m. The combination is swung in a vertical circular path on a second string, String 2, of length l = 0.500 m. During the motion, the two strings are collinear at all times as shown in Figure P6.44. At the top of its motion, m₂ is traveling at v = 4.00 m/s. (a) What is the tension in String 1 at this instant? (b) What is the tension in String 2 at this instant? (c) Which string will break first if the combination is rotated faster and faster?

Figure P6.44

pembahasan soal nomor 5:

Berdasarkan soal dapat diketahui
m₁ = 4,00 kg
m₂ = 3,00 kg
R = 0,5 m
v = 4,00 m/s
gambar diagram gaya untuk kedua benda dapat digambarkan sebagai berikut

Berdasarkan gambar di atas, kita dapat menuliskan persamaan gaya sentripetalnya sebagai berikut
Untuk benda 1 :

Dimana v₁ = 2v, R₁ = 2l
Untuk benda 2 :

Dimana v₂ = v, R₂ = l
a. Untuk menentukan besar tegangan pada tali 1, kita dapat menggunakan persamaan (1)

b. Untuk menentukan besar tegangan pada tali 1, kita dapat menggunakan persamaan (2)

c. Karena T2 > T1, maka tali 2 akan putus lebih dahulu ketika keduanya diputarkan semakin cepat

Demikian artikel kali ini tentang gaya sentripetal pada benda terhubung tali penjelasan lengkap dengan soal latihan dan pembahasan lengkap. Semoga dapat bermanfaat bagi para pembaca dan jika ada request dari para pembaca terkait materi atau soal tentang suatu bab fisika silahkan tinggalkan komentar

Mengenal frinji pada interferensi celah ganda (Gelombang Cahaya)

Pada interferensi celah ganda gelombang cahaya akan terbentuk pola gelap dan terang seperti yang digambarkan sebagai berikut.

Pola terang dan gelap yang terbentuk sebagai hasil dari interferensi konstruktif dan destruktif. Dimana y merupakan jarak terang atau gelap dari terang pusat (TP) sedangkan ∆y adalah jarak antar terang yang berdekatan (misalkan terang 1 ke terang 2, terang 2 ke terang 3, dst) atau jarak antar gelap yang berdekatan (misalkan gelap 1 ke gelap 2, gelap 2 ke gelap 3, dst) dan ½ ∆y adalah jarak antar terang dan gelap yang berdekatan (misalkan dari terang 1 ke gelap 1, dari gelap 1 ke terang 2, dari terang 2 ke gelap 3, dst). Seperti yang telah dijelaskan pada materi interferensi celah ganda pada gelombang cahaya, persamaan matematis berkaitan dengan pola terang adalah

d sin θ = mλ ... (m = 0, ±1, ±2, ±3, ...)

dy = mλR

y = mλR/d

persamaan matematis berkaitan dengan pola gelap adalah 

d sin θ = (m + ½)λ ... (m = 0, ±1, ±2, ±3, ...)

dy = (m + ½)λR

y = (m + ½)λR/d

Frinji sendiri merupakan jarak antar terang yang berdekatan atau jarak antar gelap yang berdekatan (∆y), sehingga lebar frinji ini adalah selisih antara jarak pola terang yang berdekatan (terang 1 dan 2, terang 3 dan 4, dst) ke pola terang pusat. Misalkan untuk mengetahui lebar frinji kita menggunakan selisih antara jarak terang kedua dan pertama terhadap terang pusat. Secara matematis dapat ditulis

∆y = y₂ – y₁ (boleh y₃ – y₂, y₄ – y₃)

∆y = m₂λR/d – m₁λR/d

∆y = 2λR/d – 1λR/d

 

Dimana :

∆y = frinji atau jarak antar terang atau gelap yang berdekatan (m)

λ = panjang gelombang (m)

R = jarak celah ke layar (m)

d = jarak antara kedua celah (m)

dari persamaan di atas, tentunya kita dapat menentukan bahwa jarak antar terang dan gelap yang berdekatan adalah setengah dari jarak antar terang atau gelap yang berdekatan.

 

konsep ini akan sangat berguna jika kita diminta untuk menentukan jarak antar terang atau dari terang ke n sampai gelap ke m. untuk lebih memahami konsep ini silahkan dibuka latihan soal tentang interferensi cahaya celah ganda.

Penurunan rumus koefisien restitusi (e) | konsep fisika

Dalam materi tentang impuls momentum, kita mengenal sebuah istilah yang disebut dengan “koefisien restitusi” yang mana koefisien restitusi merupakan negatif perbandingan antara kecepatan relatif sesaat sesudah tumbukan dengan kecepatan relatif sesaat sebelum tumbukan pada tumbukan satu dimensi. Selain itu dapat pula di katakan bahwa koefisien restitusi menunjukkan “tingkat terpantul” benda setelah tumbukan, semakin besar koefisien restitusinya maka tingkat terpantulnya juga akan semakin besar jadi kedua benda setelah bertumbukan akan semakin terpantul atau kehilangan energi kinetiknya semakin kecil, sebaliknya semakin kecil koefisien restitusinya maka tingkat terpantul benda setelah tumbukan semakin kecil atau kehilangan energi kinetiknya akan semakin besar. nilai koefisien restitusi terbesar adalah 1 dan terkecil adalah 0, berdasarkan nilai koefisien restitusi ini kita dapat membedakan tumbukan menjadi tiga jenis yakni tumbukan lenting sempurna, tumbukan lenting sebagian, dan tumbukan tidak lenting sama sekali.
Tumbukan lenting sempurna memiliki nilai koefisien restitusi paling besar yaitu bernilai 1 (e = 1) hal ini menunjukkan benda setelah bertumbukan akan saling terpantul dengan maksimal dan tidak ada kehilangan energi kinetik sehingga pada tumbukan lenting sempurna berlaku hukum kekekalan energi kinetik, tumbukan lenting sebagian memiliki nilai koefisien restitusi yang bervariasi antara 0 sampai 1 (0 < e < 1) yang mana pengaruh besar kecilnya koefisien restitusi ini sudah di jelaskan di atas, sedangkan untuk tumbukan tidak lenting sama sekali memiliki nilai koefisien restitusi sama dengan 0 (e = 0) hal ini menunjukkan kedua benda setelah bertumbukan tidak akan terpantul, akan tetapi bergerak bersama – sama. untuk lebih memahami materi tentang tumbukan bisa di baca di sini.

Konsep Fisika | Hukum Newton Pada Benda dihubungkan Katrol

Pada kesempatan kali ini kita akan menganalisis sistem dengan benda yang terhubung dengan katrol dengan menggunakan hukum Newton. kita fokuskan untuk katrol yang licin sehingga tidak berputar agar fokus pada penerapan hukum Newtonnya. Ada banyak variasi sistem yang menggunakan katrol dan pertanyaan yang diajukan bisa berupa menentukan percepatan sistem maupun tegangan tali. Khusus untuk tegangan tali perlu diperhatikan selama talinya masih sama (satu tali) besar tegangan talinya sama, pada kesempatan kali ini kita hanya akan membahas beberapa sistem dasar saja yang nantinya bisa dikembangkan sendiri karena alur berpikir dan cara analisanya sama. perhatikan beberapa gambar berikut.

Konsep Fisika | Hukum Newton pada Bidang Miring

Soal terkait benda pada bidang miring ada beberapa variasinya mulai dari yang paling sederhana sampai pada yang lebih rumit, akan tetapi meskipun begitu cara analisis dan alur berpikirnya tetap sama yakni gambar terlebih dahulu gaya – gaya yang bekerja pada sistem, tentukan arah gerak benda (jika bergerak) kemudian menggunakan hukum I Newton atau hukum II Newton. Hal yang membedakan pada soal benda pada bidang miring adalah letak sumbu koordinat (x, y), jika pada bidang datar sumbu koordinat ini dalam arah vertikal dan horizontal maka untuk bidang miring posisi sumbu koordinatnya mengikuti bidangnya (miring juga). Perhatikan gambar berikut.

Konsep Fisika | Gaya pada benda di dalam Lift

Salah satu penerapan hukum Newton yang sering di bahas adalah terkait dengan analisis gaya benda ketika terletak di dalam lift. Beberapa jenis gaya ketika berada di dalam lift antara lain gaya desakan benda terhadap lantai (sama dengan gaya normal) dan gaya tegang tali (untuk benda yang digantung). Untuk menganalisis soal terkait dengan gaya pada benda di dalam lift kita harus menggambarkan gaya – gaya yang bekerja pada sistem kemudian dapat menerapkan hukum I Newton untuk kondisi benda diam dan hukum II Newton untuk kondisi benda bergerak dengan percepatan tertentu.

Benda diletakkan di dasar lift

Ketika benda diletakkan dalam sebuah lift yang bergerak, ternyata benda mengalami perubahan gaya normal (gaya lantai karena berat benda) dapat semakin besar atau semakin kecil. Hal ini bergantung pada gerak lift tersebut, untuk lebih jelasnya perhatikan gambar berikut

Konsep Fisika | Gaya tegang tali dan gaya kontak

Salah satu penerapan hukum Newton yang sering di bahas adalah terkait dengan gaya tegang tali dan gaya kontak pada benda. gaya tegang tali merupakan gaya pada tali saat tali tegang karena menarik benda atau di tarik dengan gaya tertentu sedangkan gaya kontak merupakan gaya normal ketika dua benda saling bersentuhan. Untuk menganalisis soal terkait dengan gaya tegang dan gaya kontak kita harus menggambarkan gaya – gaya yang bekerja pada sistem kemudian dapat menerapkan hukum I Newton untuk kondisi benda diam dan hukum II Newton untuk kondisi benda bergerak dengan percepatan tertentu

Benda dihubungkan Tali

Gaya tegang tali adalah gaya tegang yang bekerja pada ujung-ujung tali karena tali tersebut tegang. Gaya ini akan muncul ketika pada ujung-ujung tali tersebut diberikan sebuah gaya (bisa gaya tarik, gaya berat atau yang lainnya). Perhatikan contoh beberapa benda yang dihubungkan dengan tali berikut ini.

Penggambaran gaya tegang tali (T) dengan arah bolak – balik menunjukkan adanya pasangan gaya aksi – reaksi (hukum III Newton) antara tali dengan benda, penggunaannya bergantung pada tinjauan kita.

Analisis gambar 1

Gambar (1) menunjukkan benda D dalam posisi diam yang disebabkan adanya keseimbangan antara gaya tegang tali (berarah ke atas) dengan gaya berat (w_D) yang berarah ke bawah. Besar kedua gaya ini adalah sama tetapi berlawanan arah, sehingga berdasarkan hukum I Newton kita dapat menulis

ΣF = 0

T – w_D = 0

T = w_D

T = m_D . g

Analisis gambar 2

Gambar (2) menunjukkan sebuah sistem dimana tiga buah benda masing – masing benda A, benda B, dan benda C yang dihubungkan dengan tali dan ditarik dengan gaya sebesar F pada lantai licin sehingga sistem bergerak dengan percepatan a searah dengan arah gaya F.

Hal pertama yang perlu dipahami adalah sistem bergerak dengan percepatan a, yang artinya semua benda dalam sistem (A, B, dan C) bergerak dengan percepatan sama. oleh karena itu besar percepatan menjadi faktor yang sangat penting untuk menganalisis soal jenis ini. Untuk menentukan besar percepatan sistem kita dapat menggunakan hukum II Newton yakni

ΣF = m_tot . a

ΣF = (m_A + m_B + m_C) . a

Dengan mengetahui percepatan sistem, kita dapat menentukan besar tegangan tali pada masing – masing tali penghubung antar benda (T₁ dan T₂). Tapi sebelum itu perlu diperhatikan bahwa untuk menentukan besar tegangan tali ini, kita tetap menggunakan prinsip hukum II Newton dengan memperhatikan benda yang ditarik oleh tali yang ingin dicari besarnya. Perhatikan gambar berikut

Perhatikan gambar (1) di atas, gaya tegangan tali T₁ hanya digunakan untuk menarik benda A sehingga dengan hukum II Newton kita dapat menuliskan

ΣF = m_A . a

T₁ = mA . a (substitusikan nilai "a" pada persamaan di atas)

Gambar (2) menunjukkan bahwa tegangan tali T₂ digunakan untuk menarik benda A dan benda B. Maka dengan cara yang sama untuk mencari T₁, kita dapat menentukan nilai T₂ sebagai berikut

ΣF = (m_A + m_B) . a

T₂ = (m_A + m_B). a (substitusikan nilai "a" pada persamaan di atas)

Pengembangan dari soal jenis ini adalah adanya gaya gesek antara benda dengan lantai (pada contoh di atas, dianggap lantai licin sehingga tidak ada gaya gesek). Misalkan untuk sistem sama seperti di atas, akan tetapi terdapat gaya gesek kinetik (koefisien gesek kinetisk = μ) antara benda dengan lantai seperti yang ditunjukkan oleh gambar berikut

Perhatikan pada gambar di atas, arah gaya gesek berlawanan dengan arah gerak benda (benda bergerak ke kanan sedangkan arah gaya gesek ke kiri). Pada dasarnya untuk menganalisis soal tipe ini tidak jauh berbeda dengan yang sebelumnya (tanpa gaya gesek) dimana percepatan sistem menjadi faktor penting yang dapat ditentukan menggunakan hukum II Newton dan perhatikan benda yang ditarik oleh oleh tali untuk menentukan besar gaya tegang tali.

Gaya gesek akan mempengaruhi resultan gaya pada hukum II Newton sehingga mempengaruhi bentuk persamaan matematis yang dihasilkan. Besar gaya gesek sendiri dapat ditentukan dengan persamaan

f = μ N

f = μ mg

dengan mengetahui besar gaya gesek tersebut maka bentuk hukum II Newton untuk menentukan percepatan sistem akan menjadi

ΣF = m_tot . a

F – f_A – f_B - f_C = (m_A + m_B + m_C) . a

F – μ m_A g – μ m_B g - μ m_C g = (m_A + m_B + m_C) . a

F – μ g (m_A + m_B + m_C) = (m_A + m_B + m_C) . a

Untuk menentukan besar gaya tegang tali T₁ maka persamaannya menjadi

ΣF = m_A . a

T₁ – f_A = m_A . a 

T₁ – μ m_A g = m_A . a 

T₁ = m . a + μ m_A g

Sedangkan untuk mencari gaya tegang tali T2 persamaannya menjadi ΣF = (m_A + m_B) . a

T₂ – f_A – f_B = (m_A + m_B) . a 

T₂ – μ m_A g - μ m_B g = (m_A + m_B). a

T₂ - μg (m_A + m_B) = (m_A + m_B). A

T₂ = (m_A + m_B). a + μg (m_A + m_B)

Gaya kontak antar benda

Gaya kontak antar benda yang dimaksudkan disini adalah gaya normal dari satu benda ke benda lainnya pada permukaan yang saling bersentuhan. Perhatikan gambar berikut

Perhatikan gambar (1) di atas, gaya Normal akan muncul pada bagian antara benda A dan benda B yang saling bersentuhan. Gaya inilah yang kemudian disebut dengan gaya kontak benda A dan benda B. secara keseluruhan gaya – gaya yang bekerja pada sistem tersebut dapat digambarkan sebagai berikut

Berdasarkan gambar di atas terlihat pada benda B terdapat dua buah gaya vertikal yakni gaya berat dari benda B (w_B) yang berarah ke bawah dan gaya normal pada benda B karena benda A (N_BA) yang berarah ke atas sedangkan pada benda A terdapat tiga buah gaya vertikal yakni gaya berat benda A (w_A) yang berarah ke bawah, gaya normal benda A karena benda B (N_AB) yang berarah ke bawah dan gaya normal benda A karena lantai (N_Al) yang berarah ke atas. perlu dipahami disini bahwa gaya kontak pada sistem ada dua yakni gaya kontak antara benda A dan benda B yang merupakan gaya normal antara benda A dan benda B (N_AB dan N_BA) kedua gaya ini merupakan pasangan gaya aksi – reaksi sesuai dengan hukum III Newton dan gaya kontak antara benda A dengan lantai yang merupakan gaya normal pada benda A karena lantai (N_Al)). 

Penjelasan di atas menunjukkan bahwa gaya kontak merupakan gaya normal itu sendiri, sehingga untuk menentukan besar gaya kontak pada dasarnya sama dengan ketika menentukan besar gaya normal. Besar gaya normal ini bergantung pada posisi benda dan gaya – gaya pada benda tersebut, misalkan kita akan menentukan besar gaya kontak antara benda A dan benda B maka kita harus mencari besar gaya normal pada kedua benda tersebut. karena gaya normal ini bekerja pada dua benda maka kita dapat memilih salah satu benda saja untuk ditinjau yang sekiranya paling mudah. Berdasarkan hal tersebut untuk menentukan gaya kontak antara benda A dan benda B kita akan meninjau benda B, karena benda B dalam posisi diam maka berlaku hukum I Newton yakni

ΣF = 0

N_BA – w_B = 0

N_BA = w_B

Karena kedua gaya normal pada benda A dan benda B merupakan pasangan gaya aksi – reaksi maka besar kedua gaya normal ini sama (N_BA = N_AB). Sedangkan untuk menentukan gaya kontak antara benda A dengan lantai, kita dapat meninjau benda A dimana ada tiga gaya vertikal yang bekerja padanya dan benda A dalam posisi diam, sehingga berlaku hukum I Newton sebagai berikut

ΣF = 0

N_Al – w_A – N_AB = 0

N_Al = w_A + N_AB

N_Al = w_A + N_BA

N_Al = m_Ag + m_Bg

Jika kita perhatikan lebih jauh ternyata untuk benda bertumpuk seperti itu besar gaya kontak (gaya normal) sama dengan total gaya berat benda di atasnya.

Perhatikan kembali gambar (2) di atas, posisi benda berbeda dengan sebelumnya (horizontal) benda C dan benda D yang menempel pada posisi mendatar dan di dorong dengan gaya F mendatar ke arah kanan sehingga sistem bergerak ke kanan dengan percepatan sebesar a. gaya – gaya yang bekerja pada sistem dapat dilihati pada gambar berikut

Gaya kontak yang terjadi pada kedua benda merupakan gaya Normal pada bagian yang menempel seperti pada gambar di atas. Gaya normal pada benda C karena benda D (N_CD) berarah ke kiri 

sedangkan gaya normal pada benda D karena benda C (N_DC) berarah ke kanan hal ini sesuai dengan konsep bahwa gaya Normal merupakan gaya yang tegak lurus bidang. Menganalisis sistem ini sama halnya pada sistem sebelumnya (benda dihubungkan tali) yakni percepatan menjadi faktor yang penting sehingga kita harus menentukan terlebih dahulu besar percepatan sistem dengan menggunakan hukum II Newton sebagai berikut.

ΣF = m_tot . a

F = (m_C + m_D). a

Besar percepatan ini sama untuk semua benda dalam sistem (benda C dan benda D), sedangkan besar gaya kontak kedua benda dapat ditentukan dengan meninjau benda D, dimana pada benda D hanya berlaku satu gaya yakni gaya Normal benda D karena benda C (N_DC) dengan menggunakan hukum II Newton pada benda D maka kita dapat menuliskan persamaan sebagai berikut

ΣF = m_D . a

N_DC = m_D . a (substitusikan nilai percepatan dari persamaan di atas)

Jika pada sistem terdapat gaya gesek antara benda dengan lantai maka untuk menganalisisnya dapat dilakukan dengan cara yang sama seperti pada benda yang dihubungkan tali.

demikian pembahasan ringkas terkait dengan gaya tegang tali dan gaya kontak pada benda, semoga bisa memberikan pengetahuan baru bagi para pembaca dan jika ada pertanyaan, saran, atau kiritk bisa dituliskan di kolom komentar.

Konsep Fisika tentang Penerapan Hukum Newton :

Benda di dalam lift | Bidang Miring | Benda Terhubung Katrol 

Penerapan Hukum Bernoulli lengkap dengan penurunan rumus | Fisika kelas 11

Hukum Bernoulli merupakan salah satu sub materi pokok dalam materi fluida dinamis (fisika kelas 11). Pada saat mempelajari materi fluida dinamis sangat penting untuk memahami hukum Bernoulli. Penerapan hukum Bernoulli dalam kehidupan sehari-hari biasanya tidak disertai dengan penuruan rumusnya secara lengkap merupakan permasalahan tersendiri yang sering dipelajari dalam materi fluida dinamis beberapa diantaranya adalah: kebocoran tangki, venturimeter, tabung pitot, dan gaya angkat pesawat . Secara matematis hukum Bernoulli dapat ditulis

praktikum virtual gerak parabola (fisika kelas 10)

Praktikum virtual gerak parabola dengan memanfaatkan lab virtual ini merupakan salah satu variasi pembelajaran Di masa pandemi seperti sekarang yang pembelajaran lebih banyak dilakukan secara daring atau istilahnya PJJ (pembelajaran jarak jauh). Berdasarkan pengamatan penulis, PJJ lebih banyak dilakukan dengan memberikan materi dan mengerjakan soal. Praktikum ini untuk melengkapi materi gerak parabola, latihan soal fisika gerak parabola beserta pembahasannya dan pengembangan dari materi gerak parabola yakni gerak parabola pada bidang miring, Berikut bentuk LKS yang telah dibuat. Semoga bermanfaat

Penurunan rumus momen inersia berbagai benda (lengkap dengan penjelasannya)

Daftar Isi

• Konsep rapat massa
• Sistem koordinat silinder dan sistem koordinat bola
• Sistem koordinat silinder
• Sistem koordinat bola
• Teorema sumbu sejajar
• Teorema sumbu tegak lurus
• Penurunan rumus momen inersia berbagai benda
• Batang silinder pejal
• Pelat tipis
• Silinder
• Bola
• Ekstra TIme
• Segitiga
• Kerucut

Gambar 1. Momen inersia berbagai benda

Saat mempelajari materi dinamika rotasi, tentu kalian pernah melihat gambar di atas ,Tapi pernahkah kalian berpikir asal dari persamaan-persamaan di atas? Berdasarkan hasil literasi dari berbagai sumber yang ada , Pada kesempatan kali ini saya akan mencoba melakukan penurunan rumus momen inersia untuk berbagai benda di atas sehingga ditemukan rumus-rumus dan angka di atas.

Penurunan rumus momen inersia untuk berbagai benda di atas, pada dasarnya menggunakan persamaan umum momen inersia yang sudah pernah saya bahas di metari dinamika rotasi untuk kelas 11 yakni

Persamaan di atas, merupakan persamaan dasar untuk semua jenis benda dengan massa yang terdistribusi kontinu, selain itu juga diperlukan konsep-konsep pendukung agar persamaan tersebut dapat menghasilkan rumus momen inersia untuk berbagai benda. Salah satu konsep matematis dasar yang perlu dipahami dalam menganalisis persoalan fisika adalah konsep perbandingan selain itu, Beberapa konsep lain khusus pembahasan ini yang menurut saya perlu dipahami antara lain

Konsep rapat massa

Konsep rapat massa yang saya maksudkan disini adalah kerapatan massa terhadap suatu besaran lain yakni rapat massa terhadap panjang (biasa disebut dengan satuan massa persatuan panjang). Ada tiga rapat massa yang perlu dipahami disini seperti yang ditunjukkan tabel berikut.

Konsep rapat massa ini digunakan untuk mensubstitusi nilai “dm” pada persamaan umum di atas, perhatikan juga jenis bendanya (1 dimensi, 2 dimensi, atau 3 dimenssi).

Sistem koordinat silinder dan sistem koordinat bola

Koordinat silinder dan koordinat bola sangat penting untuk dipahami, karna sebagian besar benda yang akan diturunkan rumus momen inersianya adalah benda-benda dengan bentuk silinder dan bola seperti: silinder pejal, silinder berongga, bola pejal, bola berongga dll. benda-benda tersebut akan lebih mudah dianalisis menggunakan sistem koordinat silinder dan sistem koordinat bola. Berikut gambar dan transformasi kedua sistem tersebut

Sistem koordinat silinder

Gambar 2. Koordinat silinder

Sistem koordinat bola

Gambar 3. Koordinat bola

Teorema sumbu sejajar

Teorema sumbu sejajar dapat digunakan untuk menentukan momen inersia suatu benda ketika sumbu porosnya tidak terletak pada pusat massa tetapi sejajar dengan sumbu poros melalui pusat massanya, teorema untuk sudah saya bahas di materi dinamika rotasi. Secara matematis dapat ditulis

Teorema sumbu tegak lurus

Teorema sumbu tegak lurus artinya sumbu poros yang tegak lurus sumbu melalui pusat massa yang tegak lurus penampang. Teorema ini memungkinkan menentukan momen inersia ketika sumbu porosnya tegak lurus penampang (sumbu z)dengan memanfaatkan momen inersia untuk poros tegak lurus lainnya (terhadap sumbu x dan sumbu y). Perhatikan gambar berikut

Gambar 4. Teorema sumbu tegak lurus

I_z = ∫ r² dm
I_z = ∫ (x² + y²) dm
I_z = ∫ x² dm + ∫ y² dm

Penurunan rumus momen inersia berbagai benda

Berikut penurunan rumus momen inersia berbagai benda

Batang silinder pejal

Poros melalui titik pusat massanya

Perhatikan gambar berikut, untuk mempermudah menurunkan rumusnya

Batang yang bermassa m dan memiliki panjang L dengan pusat massa berada di titik O (berada di sumbu y), tampak seperti gambar di atas. Tentukan terlebih dahulu elemen massanya (kotak warna kuning) yang memiliki ukuran dx dan berjarak x dari pusat massanya.
dm = λ dx
r = x
dengan batas integrasi
x : - ½ L sampai ½ L
sehingga

Poros melalui salah satu ujung

Perhatikan kembali gambar di atas, jika sumbu poros di geser ke tepi (sumbu y’) maka kita dapat menggunakan teorema sumbu sejajar untuk menemukan momen inersianya, dimana sumbu poros bergeser sejauh ½ L
I = I_pm + md²
I = 1/12 mL² + m( ½L)²
I = 1/12 mL² + ¼ mL²
I = 1/12 mL² + 3/12 mL²
I = 4/12 mL²
I = 1/3 mL² (terbukti)

Pelat tipis

Poros sepanjang tepi (salah satu sisinya)

Perhatikan gambar berikut

Plat tipis yang bermassa m dan memiliki panjang dan lebar berturut-turut adalah b dan a. Jika pelat tersebut diputar dengan poros sejajar salah satu sisi (b) melewati titik pusat massanya (p), maka untuk menentukan momen inersianya pertama-tama kita tentukan terlebih dahulu elemen massa dm yang memiliki panjang b dan lebar dy terletak sejauh y dari poros yang tampak seperti gambar di atas. Sehingga dapat kita tulis dm = λ dy
r = y
dengan batas integrasi
y : - ½ a sampai ½ a
sehingga

Dengan cara yang sama kita dapat menentukan momen inersia ketika porosnya sejajar dengan sisi a dan melewati titik pusat massanya yakni sebesar

Poros di pusat massanya dan tegak lurus bidang

Momen inersia pelat dengan sumbu poros di pusat massanya dan tegak lurus lurus bidang dapat ditentukan dengan menggunakan teorema sumbu tegak lurus

Berdasarkan gambar di atas, maka dapat kita ketahui bahwa momen inersia pada sumbu y sama dengan momen inersia pada pers (1) dan momen inersia pada sumbu x sama dengan momen inersia pada pers (2) sehingga dapat kita tuliskan
I_z = I_x + I_y
I_z = 1/12 mb² + 1/12 ma²
I_z = 1/12 m (a² + b²) (terbukti)

Poros sepanjang tepi (salah satu sisinya)

Momen inersia pelat sepanjang tepi salah satu sisinya dapat ditentukan dengan menggunakan teorema sumbu sejajar, dimana poros sejajar dan bergeser sejauh ½ a dari poros dipusat massanya (pers. 2), maka dapat kita tuliskan
I = I_pm + md²
I = 1/12 ma² + m( ½a)²
I = 1/12 ma² + ¼ ma²
I = 1/12 ma² + 3/12 ma²
I = 4/12 ma²
I = 1/3 ma² (terbukti)

Silinder

Silinder berongga

Sebuah silinder yang bermassa m dan panjang L memiliki lubang di tengah-tengahnya dengan jari-jari seperti tampak pada gambar a. jika silinder tersebut berotasi dengan sumbu poros melalui pusat massanya, maka momen inersianya dapat ditentukan sebagai berikut dm = ρ dV
dm = ρ r dr dθ dz (sistem koordinat silinder)
dengan batas integrasi
r : R₁ sampai R₂
θ : 0 sampai 2π
z : 0 sampai L

Sehingga

Silinder pejal

Momen inersia silinder pejal dapat ditentukan ketika nilai R₁ pada persamaan (3) sama dengan nol dan R₂ sama dengan R (jari-jari silinder), sehingga dapat ditulis

Silinder tipis berongga

Momen inersia silinder tipis berongga dapat ditentukan ketika nilai R₁ = R₂ = R, silinder hanya memiliki kulit tipis. Maka persamaan (3) dapat ditulis.

Bola

Bola pejal dengan poros melalui pusat massa

Momen inersia bola pejal dengan poros melalui pusat massa, dapat ditentukan dengan menggunakan sistem koordinat bola sehingga elemen massanya dapat ditulis sebagai berikut
dm = ρ dV
dm = ρ r² sin θ dr dθ dϕ (koordinat bola)
r = r sin θ
dengan batas integrasi
r : 0 sampai R
θ : 0 sampai π
ϕ : 0 sampai 2π
Sehingga

Bola pejal dengan poros di tepi

Momen inersia bola pejal dengan poros di tepi dapat ditentukan dengan teorema sumbu sejajar dengan poros bergeser sejauh R dari poros pusat massanya, sehingga
I = Ipm + md²
I = 2/5 mR² + m(R)²
I = 2/5 mR² + mR²
I = 7/5 mR² (terbukti)

Bola tipis berongga

Momen inersia bola tipis berongga yang dimaksudkan disini adalah sebuah bola yang terlapisi oleh sebuah kulit tipis (seperti bola pingpong), maka dalam menentukan nilai elemen massa (dm) tidak menggunakan volume akan tetapi luas permukaan bola.
dm = σ r² sin θ dθ dϕ dA
r = r sin θ
dengan batas integrasi
θ : 0 sampai π
ϕ : 0 sampai 2π
sehingga

Ekstra TIme

Segitiga

Sebuah segitiga sama sisi yang memiliki panjang sisi sebesar a diputar dengan poros berada pada satu sisi, tampak seperti gambar berikut

Elemen massa diambil lebar dy dan berjarak y dari sumbu poros. Karena nilai p berubah untuk setiap perubahan y maka, nilai p dapat ditentukan dengan persamaan

dm = σ dA (dA = p dy)
dm = σ p dy
r = y
dengan batas integrasi
y : 0 sampai h
sehingga

Kerucut

Tentukan momen inersia sebuah kerucut yang memiliki tinggi h sama dengan jari-jari alasnya r (h=r) yang diputar dengan sumbu poros z tampak seperti gambar berikut

Untuk menentukan momen inersia kerucut di atas, pertama-tama perlu diketahui bahwa kerucut tersebut terbentuk dengan menarik luasan alas (lingkaran) dari z = 0 sampai z = h. Setiap perubahan h jari-jarinya juga berubah dari r = 0 sampai r = h, sehingga dapat dikatakan batas untuk jari-jari tersebut adalah dari r = 0 sampai r = z. Selain itu, kita harus menggunakan sistem koordinat silinder untuk menentukan elemen massanya yang dapat dituliskan dm = ρ r dr dθ dz
r = r
dengan batas integrasi
r : 0 sampai z
θ : 0 sampai 2π
z : 0 sampai h
sehingga

Demikian penurunan rumus momen inersia untuk berbagai benda, semoga dapat menambah pengetahuan para pembaca dan tidak membingungkan. Jika ada kritik dan saran bisa tinggalkan komentarnya di bawah.Agar pemahamannya lebih lengkap perlu diketahui Materi ini hanya sebagian dari materi fisika dinamika rotasi 

baca juga : 
materi fisika kelas 11 : fluida statis
latihan soal fisika kelas 11 materi dinamika rotasi lengkap dengan pembahasannya
konsep fisika : pembiasan cahaya pada permukaan lengkung
konsep fisika : gerak parabola pada bidang miring