Pada kesempatan kali ini kita akan menganalisis sistem dengan benda yang terhubung dengan katrol dengan menggunakan hukum Newton. kita fokuskan untuk katrol yang licin sehingga tidak berputar agar fokus pada penerapan hukum Newtonnya. Ada banyak variasi sistem yang menggunakan katrol dan pertanyaan yang diajukan bisa berupa menentukan percepatan sistem maupun tegangan tali. Khusus untuk tegangan tali perlu diperhatikan selama talinya masih sama (satu tali) besar tegangan talinya sama, pada kesempatan kali ini kita hanya akan membahas beberapa sistem dasar saja yang nantinya bisa dikembangkan sendiri karena alur berpikir dan cara analisanya sama. perhatikan beberapa gambar berikut.
Ketiga gambar di atas merupakan contoh dari penerapan benda yang terhubung dengan katrol, cara analisis untuk ketiga gambar di atas masih sama yakni kita gambar gambar terlebih dahulu gaya – gaya yang bekerja pada sistem, kita tentukan kondisi benda (bergerak atau diam), kemudian menggunakan hukum Newton. Pada dasarnya untuk sistem benda yang terhubung katrol merupakan pengembangan dari sistem – sistem sebelumnya yang telah dijelaskan di atas, sedikit perbedaannya yakni kita bisa meninjau gerak untuk masing – masing benda terlebih dahulu sebelum kemudian dianalisis secara keseluruhan dan variabel yang menghubungkan antar benda yakni tegangan tali dan percepatan sistem.
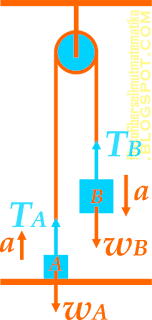
Gambar 1
Gaya – gaya yang bekerja pada sistem tersebut ditunjukkan seperti di bawah iniKarena massa benda B lebih besar dari massa benda A sehingga gaya berat benda B lebih besar daripada gaya berat benda A (wB > wA) maka benda B akan bergerak ke bawah sedangkan benda A akan bergerak ke atas. Untuk mempermudah analisis kita dapat terlebih masing – masing benda terlebih dahulu dengan menerapkan hukum II Newton seperti berikut.
Tinjau benda A
ΣFA = mA . a
TA – wA = mA . a
T – mA . g = mA . a... (1)
Tinjau benda B
ΣFB = mB . a
wB – TB = mB . a
mB . g – T = mB . a ... (2)
(TA = TB = T)
dua persamaan di atas merupakan persamaan untuk gerak masing – masing benda, dengan kedua persamaan di atas kita dapat menentukan besar percepatan sistem (sama dengan percepatan kedua benda) atau besar gaya tegang tali.
Menentukan percepatan sistem “a”
Persamaan (1) dapat kita tulis
T = mA . g + mA . a
Persamaan (2) dapat kita tulis
T = mB . g – mB . a
Kedua persamaan di atas dapat kita gabung menjadi
mA . g + mA . a = mB . g – mB . a
mB . g – mA . g = mA . a + mB . a
(mB – mA) g = (mB + mA) a
Persamaan di atas menunjukkan percepatan sistem yang juga sama dengan percepatan masing – masing benda.
Menentukan besar gaya tegangan tali “T”
Persamaan (1) dapat kita tulis
(T – mA . g)/ mA = a
Persamaan (2) dapat kita tulis
(mB . g – T)/ mB = a
Kedua persamaan di atas dapat kita gabung menjadi
T mB + TmA = mA mB g + mA mB g
T(mA + mB) = 2mA mB g
Gambar 2
ΣFC = mC . a
TC – wC = mC . a
T – mC . g = mC . a... (1)
Tinjau benda D
ΣFD = mD . a
wD – TD = mD . a
mD . g – T = mD . a ... (2)
(TC = TD = T)
Kondisi benda diam
Pada kondisi benda diam berlaku hukum I Newton untuk masing – masing benda dan gaya gesek yang bekerja adalah gaya gesek statis , sehingga tinjauan pada masing – masing benda adalah
Tinjau benda C
ΣF = 0
T – fC = 0
T = fC
T = μs mC g ... (1)
Tinjau benda D
ΣF = 0
wD – T = 0
T = mD g ... (2)
Berdasarkan persamaan (1) dan (2) kita dapat menentukan koefisien gesekan statis antara benda C dengan lantai sebagai berikut
μs mC g = mD g
μs mC = mD
Kondisi benda bergerak dengan percepatan “a”
Ketika sistem bergerak dengan percepatan a maka sama seperti pada gambar 2.1 benda C akan bergerak ke kanan sedangkan benda D akan bergerak ke kiri (karna tidak ada gaya lain yang bekerja pada benda). sehingga penerapan hukum II Newton untuk kedua benda adalah
Tinjau benda C
ΣF = mC . a
T – fk = mC . a
T – μk mC g = mC . a ... (1)
Tinjau benda D
ΣF = mD . a
wD - T = mD . a
mD g – T = mD . a... (2)
Berdasarkan kedua persamaan di atas maka kita dapat menentukan persamaan untuk menentukan percepatan sistem dan gaya tegang tali.
Menentukan percepatan sistem “a”
Persamaan (1) dapat ditulis
T = μk mC g + mC . a
Persamaan (2) dapat di tulis
T = mD g - mD . a
Kedua persamaan di atas dapat kita gabung menjadi
μk mC g + mC . a = mD g - mD . a
mC . a + mD . a = mD g - μk mC g
(mC + mD) a = (mD – μk mC) g
Menentukan gaya tegang tali “T”
Persamaan (1) dapat ditulis
T/ mC – μk g = a
Persamaan (2) dapat ditulis
g – T/ mD = a
kedua persamaan di atas dapat digabung menjadi
TmD + TmC = mC mD g + μkmC mD g
T(mD + mC) = (1+ μk) mC mD g
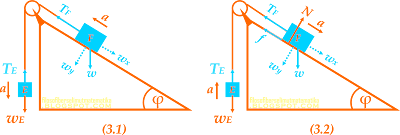
Gambar 3
ΣF = mE . a
wE – T = mE .a
mE g – T = mE .a ... (1)
Tinjau benda F
Karena benda bergerak terhadap bidang miring (sumbu x) maka kita tinjau pada sumbu x saja
T – wx = mF a
T – mFg sin φ = mF a .... (2)
Berdasarkan kedua persamaan di atas, maka kita dapat menentukan besar percepatan sistem yang juga sama untuk masing – masing benda dan menentukan besar gaya tegang tali pada sistem Menentukan besar percepatan “a”
Persamaan (1) dapat kita tulis
T = mE g – mE a
Persamaan (2) dapat kita tulis
T = mF g sin φ + mF a
Kedua persamaan di atas dapat kita gabung menjadi
mE g – mE a = mF g sin φ + mF a
mE g – mFg sin φ = mE a + mF a
(mE – mFsin φ)g = (mE + mF) a
Menentukan besar gaya tegang tali “T”
Persamaan (1) dapat ditulis
(mE g – T )/ mE = a
Persamaan (2) dapat ditulis
(T – mFg sin φ)/ mF = a
Kedua persamaan di atas dapat kita gabung menjadi
N – wy = 0
N = wy
N = mFg cos φ
Kondisi benda diam
Tapi sebelumnya perlu diperhatikan bahwa diasumsikan bahwa gaya berat wx lebih besar daripada gaya tegang tali (T) sehingga benda akan bergerak turun jika tidak ada gaya gesek, oleh karena itu arah gaya gesek searah dengan arah gaya tegang tali.
Tinjau benda E
ΣF = 0
T – wE = 0
T = wE
T = mEg ... (1)
Tinjau benda F
hukum I Newton pada sumbu x dapat ditulis.
ΣFx = 0
wx – T – fs = 0
T = wx - μs N
T = mFg sin φ - μs mFg cos φ ... (2)
Berdasarkan persamaan (1) dan (2) maka kita dapat menuliskan
mEg = mFg sin φ - μs mFg cos φ
μs mFg cos φ = mFg sin φ - mEg
μs mF cos φ = mF sin φ - mE
Kondisi benda bergerak dengan percepatan “a”
ΣF = mE . a
T – wE = mE . a
T – mE g = mE . a .... (1)
Tinjau benda F
ΣFx = mF . a
wx – f – T = mF . a
wx – μk N –T = mF . a
mFg sin φ – μk mFg cos φ – T = mF . a ... (2)
Dari persamaan (1) dan (2) kita dapat menentukan besar percepatan sistem dan besar gaya tegangan tali
Besar percepatan “a”
Persamaan (1) dapat ditulis
T = mE . a + mE g
Persamaan (2) dapat ditulis
T = mFg sin φ – μk mF cos φ – mF . a
Kedua persamaan tersebut dapat digabung menjadi
mE . a + mE g = mFg sin φ – μk mF cos φ – mF . a
mE . a + mF . a = mFg sin φ – μk mFg cos φ – mE g
(mE + mF) a = (mF sin φ – μk mF cos φ – mE) g
Besar gaya tegang tali “T”
Persamaan (1) dapat ditulis
(T – mE g)/ mE = a
Persamaan (2) dapat ditulis
(mFg sin φ – μk mFg cos φ – T)/ mF = a
Kedua persamaan di atas dapat digabung menjadi
T mF + T mE = mE mFg + mE mFg sin φ – μk mE mFg cos φ
(mF + mE)T = (1 + sin φ – μk cos φ) mE mFg









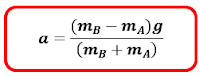





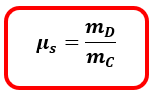




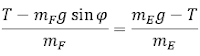







Tidak ada komentar:
Posting Komentar