Konsep Fisika | Hukum Newton pada Bidang Miring

Soal terkait benda pada bidang miring ada beberapa variasinya mulai dari yang paling sederhana sampai pada yang lebih rumit, akan tetapi meskipun begitu cara analisis dan alur berpikirnya tetap sama yakni gambar terlebih dahulu gaya – gaya yang bekerja pada sistem, tentukan arah gerak benda (jika bergerak) kemudian menggunakan hukum I Newton atau hukum II Newton. Hal yang membedakan pada soal benda pada bidang miring adalah letak sumbu koordinat (x, y), jika pada bidang datar sumbu koordinat ini dalam arah vertikal dan horizontal maka untuk bidang miring posisi sumbu koordinatnya mengikuti bidangnya (miring juga). Perhatikan gambar berikut.

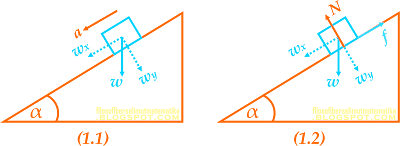
Perbedaan antara gambar (1) dan gambar (2) adalah pada gambar (1) tidak terdapat gaya luar sehingga sistem hanya dipengaruhi oleh gaya – gaya internal saja (gaya berat, gaya gesek, dan gaya normal) sedangkan untuk gambar (2) ada gaya luar sebesar F yang bekerja pada sistem hal ini nantinya yang akan membedakan bentuk persamaan matematisnya tetapi cara analisis dan alur berpikirnya tetap sama.
Soal yang sama dengan gambar (1) ada dua tipe yakni untuk lantai yang licin tanpa gesekan dan untuk lantai kasar dengan gesekan. Gaya – gaya yang bekerja pada sistem dapat digambarkan sebagai berikut

Gambar 1.1 menunjukkan lintasan licin sehingga benda akan meluncur ke bawah karena adanya gaya berat, besarnya percepatan yang dialami benda dapat ditentukan dengan menerapkan hukum II Newton pada sumbu x (karena benda hanya bergerak pada sumbu x) seperti berikut ini
ΣF_x = m a
w_x = m . a
m g sin α = m . a

Berdasarkan persamaan tersebut maka dapat diketahui bahwa percepatan benda hanya bergantung pada sudut bidang miring α.
. Pada gambar 1.2 adalah ketika lantai bidang miring kasar sehingga memiliki gaya gesek antara bidang dengan lantai. analisis soal tipe ini jika tidak ada keterangan benda bergerak atau diam maka kita harus memeriksanya terlebih dahulu apakah benda dalam posisi diam atau bergerak.
Benda akan dalam posisi diam jika gaya gesek statis maksimum lebih besar dari pada gaya berat benda terhadap sumbu x (f_smax > w_x). Sedangkan benda akan bergerak ke bawah jika gaya berat terhadap sumbu x lebih besar daripada gaya gesek statis maksimum (f_smax > w_x) sehingga gaya gesek yang bekerja adalah gaya gesek kinetis. Jadi untuk menentukan kondisi benda kita perlu menentukan besar gaya berat sumbu x dan gaya gesek statis maksimumnya.
Kondisi benda diam
Berlaku hukum I Newton
ΣF = 0
f_s – w_x = 0
f_s = w_x
μ_s N = w_x
μ_s w_y = w_x
μ_s mg cos α = mg sin α
μ_s cos α = sin α
μ_s = sin α / cos α

Persamaan di atas menunjukkan bahwa besar koefisien gesek statis pada bidang miring hanya dipengaruhi oleh besar sudut bidang miring itu sendiri.

Kondisi benda bergerak dengan percepatan “a” ke bawah
Berlaku hukum II Newton
ΣF = m . a
w_x – f_k = m . a
mg cos α – μ_k mg sin α = m . a
a = g cos α – μ_k g sin α

Persamaan di atas menunjukkan besar percepatan yang dialami benda ketika bergerak di atas bidang miring yang kasar.
Perhatikan kembali gambar 2 di atas, untuk soal jenis ini juga ada dua kondisi yakni ketika lantai licin tanpa gesekan dan ketika lantai kasar sehingga memiliki gaya gesek. Gaya – gaya yang bekerja pada sistem dapat dilihat pada gambar berikut

Pada kedua gambar di atas terlihat gaya dorong F juga diuraikan terhadap sumbu x dan sumbu y, akan tetapi jika gaya ini sudah berhimpit dengan sumbu ,i>x atau sumbu y tidak usah diuraikan lagi. Gambar (2.1) menunjukkan sistem ketika lantai licin tanpa adanya gaya gesek dan gambar (2.2) menunjukkan sistem ketika lantai kasar dengan adanya gaya gesek. Satu hal lagi yang perlu diperhatikan yakni ketika pada sistem bidang miring ada gaya luar yang bekerja (gaya dorong atau gaya gesek) maka kita harus memastikan kondisi bendanya terlebih dahulu bergerak atau diam jika pada soal tidak disebutkan kondisi bendanya.
Pada gambar (2.1) kita dapat menganalisisnya menjadi dua yakni ketika benda diam maka berlaku hukum I Newton dan ketika benda bergerak dengan percepatan a baik bergerak naik ataupun bergerak turun maka berlaku hukum II Newton.
Benda pada kondisi diam
Berlaku hukum I Newton
ΣF = 0
F_x – w_x = 0
F_x = w_x
F cos α = mg sin α

Persamaan di atas menunjukkan besar gaya dorong yang dibutuhkan untuk membuat benda diam ketika diletakkan di atas bidang miring yang licin.

Benda pada kondisi bergerak dengan percepatan “a”
Ketika benda bergerak dengan percepatan a juga memiliki dua kemungkinan, yakni benda bergerak naik dan benda bergerak turun. Hal ini bergantung pada besarnya gaya F, jika gaya F lebih besar dari pada gaya berat pada sumbu x (w_x) maka benda akan bergerak naik akan tetapi sebaliknya jika gaya F lebih kecil daripada gaya berat pada sumbu x (w_x) maka benda akan bergerak turun. Keduanya sama – sama berlaku hukum II Newton yang perlu diperhatikan adalah resultan gayanya dimana gaya yang lebih besar memiliki arah yang sama dengan arah percepatan benda.
Benda bergerak naik (F > w_x)
ΣF = m . a
F – w_x = m . a
F – mg sin α = m . a

Persamaan di atas menunjukkan percepatan benda ketika bergerak naik

Benda bergerak turun (F < w_x)
ΣF = m . a
w_x – F= m . a
mg sin α – F = m . a

Persamaan di atas menunjukkan percepatan benda ketika bergerak turun

Perhatikan kembali gambar 2.2 di atas, sama halnya dengan gambar 2.1 karena pada sistem bekerja gaya luar yakni gaya dorong F dan gaya gesek, maka kita harus menentukan terlebih dahulu kondisi benda diam atau bergerak (jika di soal belum diketahui), kondisi benda ini dapat terlihat pada resultan gaya pada sumbu x jika resultan gayanya sama dengan nol maka benda akan diam (gaya gesek yang bekerja adalah gaya gesek statis), sedangkan jika resultan gaya pada sumbu x tidak sama dengan nol maka benda akan bergerak dengan percepatan sebesar a (gaya gesek yang bekerja adalah gaya gesek kinetis). Perlu diperhatikan juga resultan gaya pada sumbu y, karena disana tidak hanya bekerja gaya berat akan tetap ada gaya luar F_y juga pada gaya normal yang bekerja pada benda tidak sama dengan gaya berat pada sumbu y. Besarnya gaya normal dapat ditentukan dengan menerapkan hukum I Newton seperti berikut ini
ΣF_y = 0
N – F_y – w_y = 0
N = F_y + w_y
N = F sin α + mg cos α ... (1)
Benda pada kondisi diam
Ketika benda berada pada kondisi diam maka gaya gesek yang bekerja adalah gaya gesek statis dan berlaku hukum I Newton seperti berikut ini
ΣF = 0
F_x + f_s – w_x = 0
F_x + f_s = w_x
F_x + μ_s N = w_x ⇒ substitusikan nilai “N” dari persamaan (1)
F cos α + μ_s (F sin α + mg cos α) = mg sin α
(bagi semua suku dengan “cos α”)
μ_s (F tan α + mg) = mg tan α – F ... (2)
Dari persamaan (2) ini kita dapat menentukan besar koefisien gesek statis dan besar gaya F seperti berikut

Menentukan koefisien gesek statis
μ_s (F tan α + mg) = mg tan α – F

Persamaan di atas menunjukkan besar koefisien gesek statis ketika benda berada pada kondisi diam dengan asumsi bahwa besar gaya F_x lebih kecil dari besar gaya berat terhadap sumbu x (w_x) sehingga benda akan turun jika tidak ada gaya gesek. Akan tetapi jika besar gaya berat w_x lebih kecil dari besar gaya F_x maka arah gaya gesek akan searah dengan gaya berat w_x sehingga benda akan naik jika tidak ada gaya gesek.

Menentukan besar gaya dorong “F”
μ_s (F tan α + mg) = mg tan α – F
μ_s F tan α + μsmg = mg tan α – F
μ_s F tan α + F = mg tan α – μs mg
F(μ_s tan α + 1) = mg (tan α – μ_s)

Persamaan di atas menunjukkan besar gaya dorong yang diperlukan agar benda berada dalam kondisi diam dengan asumsi bahwa besar gaya F_x lebih kecil dari besar gaya berat terhadap sumbu _x (w_x) sehingga benda akan turun jika tidak ada gaya gesek. Akan tetapi jika besar gaya berat wx lebih kecil dari besar gaya F_x maka arah gaya gesek akan searah dengan gaya berat w_x sehingga benda akan naik jika tidak ada gaya gesek.

Benda pada kondisi bergerak dengan percepatan “a”
sama dengan pada gambar 2.1 sebelumnya ketika benda bergerak dengan percepatan a ada dua kemungkinan yakni benda bergerak naik atau benda bergerak turun. Terdapat perbedaan pada arah gaya gesek antara benda bergerak naik dan benda bergerak turun seperti yang ditunjukkan gambar berikut

Berdasarkan kedua gambar di atas terlihat perbedaan yang jelas pada arah gaya gesek kinetis ketika benda bergerak naik dan bergerak turun, hal ini dikarenakan arah gaya gesek selalu berlawanan dengan arah gerak benda. perbedaan arah gaya gesek ini akan mempengaruhi persamaan hukum II Newton untuk kedua kondisi di atas
Benda bergerak naik dengan percepatan “a” (gambar 2.2a)
ΣF = m . a
ΣF = m . a
F_x – f_k – w_x = m a
F cos α – μ_k N – mg sin α = m . a
F cos α – μ_k N – mg sin α = m . a ⇒ substitusikan nilan “N” dari pers. (1)
F cos α – μ_k (F sin α + mg cos α) – mg sin α = m . a
F cos α – μ_k F sin α + μ_k mg cos α – mg sin α = m . a
F (cos α – μ_k sin α) + mg (μ_k cos α – sin α) = m . a

Persamaan di atas menunjukkan percepatan benda ketika benda bergerak naik

Benda bergerak turun dengan percepatan “a” (gambar 2.2b)
ΣF = m . a
w_x – f_k – F_x = m a
mg sin α – μ_k N – F cos α = m . a
mg sin α – μ_k N – F cos α = m . a ⇒ substitusikan nilan “N” dari pers. (1)
mg sin α – μ_k (F sin α + mg cos α) – F cos α = m . a
mg sin α – μ_k F sin α + μ_k mg cos α – F cos α = m . a
mg (μ_k cos α + sin α) – F (cos α + μ_k sin α) = m . a

Persamaan di atas menunjukkan percepatan benda ketika benda bergerak turun
demikian pembahasan singkat tentang penerapan hukum Newton pada bidang miring, semoga dapat memberikan manfaat bagi para pembaca dan jika ada pertanyaan, saran, atau kritik dapat dituliskan di kolom komentar di bawah ini.

Konsep Fisika tentang Penerapan Hukum Newton :

Gaya Tegang Tali dan Gaya Kontak | Benda di dalam lift | Benda Terhubung Katrol