Hukum Bernoulli merupakan salah satu sub materi pokok dalam materi fluida dinamis (fisika kelas 11). Pada saat mempelajari materi fluida dinamis sangat penting untuk memahami hukum Bernoulli. Penerapan hukum Bernoulli dalam kehidupan sehari-hari biasanya tidak disertai dengan penuruan rumusnya secara lengkap merupakan permasalahan tersendiri yang sering dipelajari dalam materi fluida dinamis beberapa diantaranya adalah: kebocoran tangki, venturimeter, tabung pitot, dan gaya angkat pesawat . Secara matematis hukum Bernoulli dapat ditulis
Keterangan :
P = tekanan (N/m2)
ρ = massa jenis fluida (kg/m3)
v = kecepatan fluida (m/s)
g = percepatan gravitasi (m/s2)
h = ketinggian (m)
Penerapan hukum Bernoulli dalam menyelesaikan permasalahan-permasalahan tersebut juga diintegrasikan dengan beberapa konsep fisika lainnya yakni: gerak parabola, tekanan hidrostatis, dan persamaan kontinuitas.Pada kesempatan kali ini saya akan mencoba untuk menguraikan penerapan hukum Bernoulli dalam kehidupan sehari-hari terutama pada kebocoran tangki, gaya angkat pesawat, venturimeter, dan tabung pitot lengkap dengan penurunan rumusnya. Selamat menikmati..
Kebocoran tangki
Penerapan hukum Bernoulli yang pertama pada kebocoran tabung seperti yang terlihat pada gambar di bawah iniPada gambar di atas ada sebuah tangki yang berisi zat cair setinggi H yang mengalami kebocoran pada jarak h1 dari permukaan sehingga air keluar dari lubang dengan kecepatan v dan mencapai jarak x dari dinding.
Menganalisis permasalahan ini selain menggunakan hukum Bernoulli (untuk titik A dan titik B) juga menggunakan konsep gerak parabola (gerak air yang keluar dari lubang). Dengan menggunakan dua konsep tersebut kita dapat menentukan berbagai hal, tapi sebelum kita menganalisis kebocoran pada tangki perlu diketahui beberapa hal yakni
H = ketinggian total fluida dalam air
h1 = kedalaman lubang (jarak dari lubang ke permukaan)
h2 = ketinggian lubang (jarak dari lubang ke dasar)
Perhatikan titik A dan titik B, hukum Bernoullinya dapat ditulis
PA + ½ ρvA2 + ρghA = PB + ½ ρvB2 + ρghB
dengan:
PA = PB = P0
vA << vB , sehingga vA ≈ 0 (kecepatan air yang turun pada titik A (vA) jauh lebih kecil daripada kecepatan air yang keluar dari lubang (vB))
sehingga, hukum Bernoullinya dapat ditulis
P0 + ρghA = P0 + ½ ρvB2 + ρghB
ρghA = ½ ρvB2 + ρghB
2g(hA – hB) = vB2
√2g(hA – hB) = vB
Gerak Parabola
Gerak parabola merupakan gerak dari air yang keluar dari lubang di samping tangki karena membentuk lintasan parabola, sehingga kita melakukan analisisnya dengan analisis gerak parabola. Untuk gambar di atas, air yang keluar dari lubang berada pada titik tertinggi dari gerak parabola sehingga kecepatannya merupakan kecepatan dalam arah sumbu x. Dalam kasus di atas, kita dapat menentukan waktu air untuk mencapai tanah dengan cara yang sama dengan menghitung waktu yang dibutuhkan benda yang bergerak parabola dari titik puncak ke tanah yakni
h = v0y + ½ gt2 (h = ketinggian lubang)
h2 = 0 + ½ gt2
Variasi dari soal jenis ini dapat dilihat seperti pada gambar berikut ini
Pada dasarnya untuk menganalisis gambar di atas, konsep yang digunakan sama dengan kasus pertama yakni dengan menggunakan persamaan Bernoulli dan gerak parabola. hanya yang perlu diperhatikan pada kasusnya ada penyesuaian seperti berikut penjelasannya.
Gambar (A)
Perbedaan analisisnya dari gambar 1 yakni lubang berada di dasar (h2 = 0) dan gerak air merupakan gerak parabola sempurna dengan sudut elevasi sebesar α, sehingga untuk menentukan kecepatan air yang keluar dari lubang perhatikan kembali persamaan (1) di atas.
√2g(H – h2) = vB (h2 = 0)
√2gh = v... (4)
Lama waktu air di udara sama dengan rumus tmax untuk gerak parabola yakni
Gambar (A)
Perbedaan analisisnya dari gambar 1 yakni lubang berada di dasar (h2 = 0) dan gerak air merupakan gerak parabola sempurna dengan sudut elevasi sebesar α, sehingga untuk menentukan kecepatan air yang keluar dari lubang perhatikan kembali persamaan (1) di atas.
√2g(H – h2) = vB (h2 = 0)
√2gh = v... (4)
Lama waktu air di udara sama dengan rumus tmax untuk gerak parabola yakni
Gambar (B)
gambar (B) menunjukkan suatu wadah dengan kebocoran di dasarnya yang terletak di atas sebuah bangunan sehingga air yang keluar membentuk lintasan parabola dan sampai ke tanah sejauh X dari dinding bangunan.
Analisis pada gambar seperti ini sebenarnya sama dengan cara analisis untuk permasalahan di awal (gambar 1), untuk menentukan air kecepatan air yang keluar dari kebocoran di dasar lubang dapat digunakan persamaan (1) yakni
√2g(H – h2) = vB
Dimana:
H = h1 = kedalaman lubang (jarak dari permukaan)
h2 = 0 (karena lubang terletak di dasar)
ingat h2 pada persamaan ini adalah ketinggian lubang dari dasar tabung
sehingga persamaan tersebut dapat ditulis
gambar (B) menunjukkan suatu wadah dengan kebocoran di dasarnya yang terletak di atas sebuah bangunan sehingga air yang keluar membentuk lintasan parabola dan sampai ke tanah sejauh X dari dinding bangunan.
Analisis pada gambar seperti ini sebenarnya sama dengan cara analisis untuk permasalahan di awal (gambar 1), untuk menentukan air kecepatan air yang keluar dari kebocoran di dasar lubang dapat digunakan persamaan (1) yakni
√2g(H – h2) = vB
Dimana:
H = h1 = kedalaman lubang (jarak dari permukaan)
h2 = 0 (karena lubang terletak di dasar)
ingat h2 pada persamaan ini adalah ketinggian lubang dari dasar tabung
sehingga persamaan tersebut dapat ditulis
√2gh1 = vB ... (7)
waktu yang dibutuhkan benda yang bergerak parabola dari titik puncak ke tanah yakni
h = v0y + ½ gt2 (h = ketinggian lubang dari dasar tanah)
h2 = 0 + ½ gt2
h = v0y + ½ gt2 (h = ketinggian lubang dari dasar tanah)
h2 = 0 + ½ gt2
Gaya angkat pesawat
Sebuah pesawat dapat terbang di angkasa karena mendapatkan gaya ke atas yang disebabkan karena adanya perbedaan tekanan di bagian bawah dan bagian atas pesawat. perhatikan gambar berikut
Gambar (A) menunjukkan sebuah pesawat yang sedang terbang, pesawat memiliki gaya berat (w) yang arahnya ke bawah agar ia dapat terbang maka harus ada gaya lain yang mampu menahan berat pesawat itu. Gaya ke atas atau juga disebut dengan gaya angkat pesawat (FA) digambarkan arah panah ke atas yang didapatkan dari perbedaan tekanan di bagian atas sayap pesawat dan tekanan pada bagian bawah pesawat. gambar (B) menunjukkan penampang sayap pesawat, gaya angkat pesawat dihasilkan dari tekanan bagian bawah pesawat lebih besar daripada tekanan di bagian atas pesawat (P2 > P1).
Perbedaan tekanan ini didapatkan dari perbedaan kecepatan udara di bagian atas dan bagian bawah sayap pesawat. jika kita perhatikan lebih cermat bagian atas pesawat lebih cembung daripada bagian bawah pesawat hal ini mengakibatkan kecepatan pada bagian atas lebih besar daripada kecepatan pada bagian bawah (v1 > v2). Karena kecepatan berbanding terbalik dengan tekanan, maka akibatnya tekanan di bagian atas pesawat lebih kecil daripada bagian bawah pesawat. konsep ini juga yang menyebabkan jika ada kereta api yang sedang melaju kita tidak boleh terlalu dekat karena kecepatan aliran udara di sekitar kereta api lebih besar daripada kecepatan lingkungannya sehingga tekanan di sekitar kereta api lebih kecil daripada di lingkunganya, jika kita berdiri terlalu dekat dari kereta maka kita akan tertarik ke arah kereta api, hal ini tentu sangat membahayakan. Oleh karena itu selalu ada batas tempat orang bisa berdiri di jalur-jalur kereta api yang terdapat di stasiun.
Besar gaya ke angkat pesawat ini dapat ditentukan dengan menerapkan hukum Bernoulli untuk bagian atas (A) dan bagian bawah (B) sayap pesawat seperti berikut ini.
PA + ½ ρvA2 + ρghA = PB + ½ ρvB2 + ρghB
Dimana hA = hB (perbedaan ketinggian bagian atas dan bawah sayap pesawat jauh lebih kecil daripada ketinggian pesawat ketika terbang)
ρ = massa jenis udarasehingga persamaan di atas dapat ditulis
PA + ½ ρvA2 = PB + ½ ρvB2
PB – PA = ½ ρvA2 - ½ ρvB2
PB – PA = ½ ρ(vA2 – vB2)
ΔP = ½ ρ(vA2 – vB2)... (i)
Selisih tekanan (ΔP) pada persamaan di atas secara matematis dapat kita tulis
ΔP = FA / A ... (ii)
Dimana
A = luas permukaan sayap pesawat
Dengan mensubstitusikan persamaan (ii) ke persamaan (i) maka kita akan mendapatkan
FA/A = ½ ρ(vA2 – vB2)
Variasi dari fenomena ini adalah ketika pesawat tersebut akan lepas landas atau mendarat, perhatikan gambar berikut
Gambar (A) menunjukkan keadaan pesawat ketika lepas landas, dimana pesawat akan bergerak ke atas dengan percepatan a, sedangkan gambar (B) menunjukkan keadaan pesawat ketika akan mendarat, dimana pesawat akan bergerak turun dengan percepatan a. Analisis dari fenomena ini pada dasar cukup mudah, kita hanya menambahkan konsep hukum II Newton (ΣF = m.a) untuk masing-masing keadaan.
ΣF = m . a (karena pesawat bergerak ke atas, maka FA > w)
FA – w = m . a
Gambar (B)
ΣF = m . a (karena pesawat bergerak ke bawah, maka w > FA)
w – FA = m . a
ΣF = m . a (karena pesawat bergerak ke bawah, maka w > FA)
w – FA = m . a
Venturimeter
Venturimeter adalah sebuah alat yang berbentuk tabung pipa dengan dua tabung sejajar digunakan untuk mengukur kecepatan fluida dalam pipa tersebut. Ada dua jenis venturimeter yakni venturimeter tanpa manometer dan venturimeter dengan manometer. Analisis kedua jenis venturimeter tersebut menggunakan hukum Bernoulli, persamaan kontinuitas dan konsep tekanan hidrostatis. Mari kita analisis satu persatu dari venturimeter tersebut.
Venturimeter tanpa manometer
Gambar di atas menunjukkan sebuah venturimeter tanpa manometer, fluida mengalir dari titik 1 menuju titik 2 yang luasnya semakin kecil sehingga menyebabkan kecepatan aliran fluida di titik 2 lebih besar daripada kecepatan aliran fluida di titik 1. Perbedaan kecepatan menyebabkan adanya perbedaan tekanan pada titik 1 dan titik 2 sehingga ketinggian air pada tabung vertikal di titik 1 dan 2 berbeda.
kita dapat menganalisisnya dengan menggunakan konsep hukum Bernoulli, tekanan hidrostatis, dan persamaan kontinuitas seperti berikut
hukum bernoulli
P1 + ½ ρv12 + ρgh1 = P2 + ½ ρv22 + ρgh2
Dimana
h1 = y1
h2 = y2
y1 = y2 (ketinggian titik 1 dan titik 2 diukur dari dasar adalah sama besar)
sehingga persamaan bernoullinya menjadi
P1 + ½ ρv12 = P2 + ½ ρv22
P1 - P2 = ½ ρ(v22 - v12)
Tekanan hidrostatis
Perbedaan tekanan pada persamaan di atas, disebabkan adanya perbedaan ketinggian pada fluida di atasnya (perhatikan pipa kecil vertikal) yakni sama dengan perbedaan tekanan hidrostatisnya, sehingga dapat ditulis
P1 – P2 = ρgh
Maka kita dapat menuliskan persamaan hukum bernoullinya menjadi
ρgh = ½ ρ(v22 - v12)
2gh = (v22 - v12) ... (1)
Persamaan kontinuitas
Untuk menentukan kecepatan aliran fluida (v1 atau v2) kita dapat menggunakan persamaan kontinuitas sebagai berikut
A1 v1 = A2 v2 ... (2)
Pada tahap ini kemudian tergantung pada soal, kecepatan mana yang akan dicari. Jika kita akan menentukan kecepatan pada titik 1, maka persamaan (2) di atas dapat diubah menjadi
v2 = (A1/A2) v1
kemudian di substitusikan ke persamaan (1), sehingga kita dapat menuliskan
Jika kita akan menentukan kecepatan pada titik 2, maka persamaan (2) di atas dapat diubah menjadi
v1 = (A2/A1) v2
kemudian di substitusikan ke persamaan (1), sehingga kita dapat menuliskan
Venturimeter dengan manometer
Gambar di atas menunjukkan sebuah venturimeter dengan manometer (manotmeter di bagian bawah), perbedaan dengan venturimeter sebelumnya terletak pada fluida yang digunakan. Jika pada venturimeter tanpa manometer menggunakan satu jenis fluida, venturimeter dengan manometer menggunakan dua jenis fluida (pada manometer terdapat fluida sendiri). sama hal nya dengan venturimeter sebelumnya, karena adanya perubahan luas pipa (penyempitan) maka kecepatan di titik 2 akan lebih cepat daripada kecepatan di titik 1, sehingga menyebabkan tekanan di titik 2 lebih kecil daripada tekanan di titik 1. Perbedaan tekanan ini menyebabkan perbedaan ketinggian fluida pada manometernya.
Kita dapat melakukan analisis dengan menggunakan hukum Bernoulli, persamaan kontinuitas, dan konsep tekanan hidrostatis.
hukum bernoulli
P1 + ½ ρAv12 + ρAgh1 = P2 + ½ ρAv22 + ρAgh2
Dimana
h1 = h2 (ketinggian titik 1 dan titik 2 diukur dari dasar adalah sama besar)
sehingga persamaan bernoullinya menjadi
P1 + ½ ρAv12 = P2 + ½ ρAv22
P1 - P2 = ½ ρA(v22 - v12)
Tekanan hidrostatis
Perhatikan a dan titik b, karena kedua titik berada dalam satu garis lurus, maka keduanya memiliki tekanan hidrostatis yang sama dengan tekanan pada masing-masing titik adalah
PA = P1 + ρAgy1
PB = P2 + ρAgy2 + ρCgh
Maka dapat kita tulis
PA = PB
P1 + ρAgy1 = P2 + ρAgy2 + ρCgh
P1 – P2 = ρCgh + ρAgy2 - ρAgy1
P1 – P2 = ρCgh + ρAg(y2-y1)
Perhatikan bahwa
y1 – y2 = h, sehingga
y2 – y1 = -h
P1 – P2 = ρCgh - ρAgh
P1 – P2 = (ρC - ρA)gh
Maka kita dapat menuliskan persamaan hukum bernoullinya menjadi
(ρC - ρA)gh = ½ ρA(v22 - v12)
2(ρC - ρA)gh = ρA (v22 - v12) ... (1)
Persamaan kontinuitas
Untuk menentukan kecepatan aliran fluida (v1 atau v2) kita dapat menggunakan persamaan kontinuitas sebagai berikut
A1 v1 = A2 v2 ... (2)
kemudian di substitusikan ke persamaan (1), sehingga kita dapat menuliskan
Jika kita akan menentukan kecepatan pada titik 2, maka persamaan (2) di atas dapat diubah menjadi
v1 = (A2/A1) v2
kemudian di substitusikan ke persamaan (1), sehingga kita dapat menuliskan
Tabung pitot
Mirip dengan venturimeter, tabung pitot juga digunakan untuk mengukur kecepatan suatu fluida, hanya pada tabung pitot fluida yang diukur hanya zat gas. Secara sederhana tabung pitot dapat digambarkan sebagai berikut
Berdasarkan gambar di atas, terlihat aliran gas yang memasuki pipa besar (1) dan sebagian juga akan memasuki pipa kecil (2) sehingga menyebabkan cairan pada bagian bawahnya akan turun hingga kedalaman tertentu. Ketika cairan tidak lagi turun maka udara yang berada pada pipa kecil (2) tidak bergerak. Kita dapat melakukan analisis dengan menerapkan hukum Bernoulli dan tekanan hidrostatis
bernoulli dan tekanan hidrostatis
Hukum bernoulli
P1 + ½ ρ1v12 + ρ1gh1 = P2 + ½ ρ1v22 + ρ1gh2
Dimana:
h1 = h2
v2 = 0
sehingga persamaan di atas dapat ditulis
P1 + ½ ρ1v12 = P2
P2 – P1 = ½ ρ1v12
P2 – P1 = ½ ρ1v2 ... (1)
Tekanan hidrostatis
Perhatikan titik a dan titik b terletak pada satu garis lurus, sehingga kedua titik tersebut memiliki tekanan yang sama yakni
Pa = ρ2gh + ρ1gy + P1
Pb = ρ1gh + ρ1gy + P2
Pa = Pb
ρ2gh + ρ1gy + P1 = ρ1gh + ρ1gy + P2
ρ2gh + P1 = ρ1gh + P2
ρ2gh - ρ1gh = P2 - P1
(ρ2 - ρ1)gh = P2 - P1 ... (2)
Substitusikan pers (2) ke pers (1)
(ρ2 - ρ1)gh = ½ ρ1v2
2(ρ2 - ρ1)gh = ρ1v2
Karena ρ2 >> ρ1, maka persamaan di atas dapat ditulis
2ρ2gh = ρ1v2
Dimana
ρ2 = massa jenis cairan
ρ1 = massa jenis gas
demikian sedikit pembahasan terkait dengan penerapan hukum Bernoulli lengkap dengan penurunan rumusnya dalam kehidupan sehari-hari untuk lebih memahami hukum Bernoulli ini silahkan dilihat latihan soal fluida dinamis untuk kelas 11 yang juga disertai dengan pembahasan secara terperinci. semoga bermanfaat.













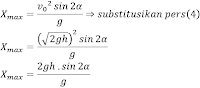























Tidak ada komentar:
Posting Komentar