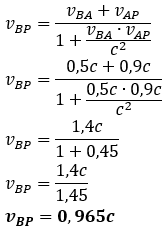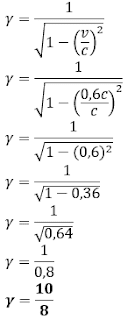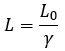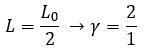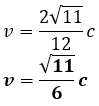Jurus Jitu : Menyelesaikan Soal Relativitas Khusus Einstein

Materi relativitas khusus Einstein dipelajari oleh siswa kelas 12 di tingkat SMA/MA pada semester 2, materi ini sering kali dianggap siswa sebagai salah satu materi yang sulit untuk dipahami apalagi menyelesaikan soal-soalnya. Kesulitan yang dialami oleh siswa dalam menyelesaikan soal relativitas khusus einstein adalah bagaimana cara mengilustrasikan soal tentang penjumlahan kecepatan relativistik dan memasukkan besaran-besaran yang diketahui ke dalam rumus yang ada, kesulitan kedua yang dialami siswa dalam menyelesaikan soal relativitas khusus Einsten menentukan besarnya kecepatan v dari tetapan γ yang diketahui atau sebaliknya. Untuk yang kedua sih, mungkin banyak yang lebih kepada malas menghitung karena menggunakan persamaan yang cukup rumit.
Jurus jitu : menyelesaikan soal relativitas khusus einstein saya buat dengan maksud untuk sharing-sharing saja karena menurut saya cara ini bisa digunakan untuk membantu dalam memahami dan menyelesaikan soal tentang relativitas Einstein. Saya tidak mengklaim Jurus jitu (atau bisa disebut cara cepat, rumus cepat bebas lah) ini bukan berarti cara yang paling baik, mungkin diantara para pembaca ada yang memiliki cara yang lebih baik bisa di sharing di kolom komentar, serta jurus jitu ini bukan berarti cocok untuk digunakan oleh semua orang, karena pemahaman tiap orang pasti berbeda-beda, silahkan digunakan jika dirasa cocok jangan digunakan jika tak cocok. Sebelum membahas jurus jitu yang akan saja jabarkan, pertama-tama perlu diperhatikan beberapa konsep, untuk mengkroscek hasil perhitungan dengan teori yang ada.

Konsep 1 :
Tidak ada kecepatan yang melebihi kecepatan cahaya (c) yakni sebesar 3 x 10⁸ m/s. sehingga kecepatan tidak mungkin bernilai lebih dari c, seperti 1,1 c, 2 c¸ 3,2 c dst.
Konsep 2 :
Nilai γ selalu lebih besar dari pada 1 (γ > 1)
Jika dalam perhitungan hasilnya tidak sesuai dengan konsep di atas, silahkan dicek kembali rumus atau perhitungannya.

Jurus Jitu Pertama : menyelesaikan soal penjumlahan kecepatan relativistik

Persamaan umum untuk penjumlahan kecepatan relativistik adalah

Keterangan :
v_AB : kecepatan benda “A” terhadap benda “B”
v_AP : kecepatan benda “A” terhadap benda “P”
v_PB : kecepatan benda “P” terhadap benda “B”

Pada persamaan di atas saya menggunakan kata “benda” untuk menunjukkan objek yang diamati, akan tetapi pada soal biasanya objek dapat berupa pesawat, planet, elektron, peluru, dll. Perhatikan penulisan persamaan di atas selalu ada tiga buah kecepatan yakni satu kecepatan di ruas kiri (yang ditanyakan) dan dua kecepatan di sebelah kanan (yang diketahui), pada bagian indeksnya jika yang ditanyakan memiliki indeks “AB” maka penulisan indeks kecepatan pada ruas kanan harus “AP + PB”, jadi dapat kita katakan untuk “membentuk” indeks “AB” maka indeks penyusunnya adalah “AP + PB” atau bisa juga “A1 + 1B” dsb bergantung pada yang diketahui di soal, namun yang penting adalah bagian tengahnya harus sama. Dalam menyelesaikan soal tentang penjumlahan kecepatan relativistik ini, tidak terlalu sulit, beberapa hal yang perlu diperhatikan adalah

• Kecepatan adalah besaran vektor
Konsep dasar tentang kecepatan adalah bahwa kecepatan merupakan besaran vektor yang mana perlu memperhatikan arahnya. untuk dua benda yang bergerak searah maka kecepatannya sama-sama bernilai positif, sedangkan untuk dua benda yang bergerak berlawanan arah maka salah satu kecepatannya bernilai negatif dan yang lain bernilai positif
• Kecepatan adalah besaran vektor
Peng”indeks”an besaran kecepatan harus sesuai dengan soal, hal ini penting untuk dilakukan agar tidak salah dalam memasukkan ke dalam persamaan, serta dalam memberikan indeks saya pribadi tidak harus selalu menggunakan indeks “1, 2, A, atau B” pemberian indeks disesuaikan dengan soalnya.
Contoh :
Pesawat terbang A bergerak dengan kecepatan v relatif terhadap planet Bumi. Penulisan kecepatannya adalah v_AB
Sebuah peluru ditembakkan dari pesawat 1 dengan kecepatan sebesar v relatif terhadap pesawat 1. Penulisan kecepatannya adalah v_P1
• Sifat indeks
Sifat indeks yang dimaksudkan disini adalah jika penulisan indeksnya dibalik maka kecepatannya akan bernilai negatif, perhatikan contoh berikut ini.
v_AB = -v_BA
v_BP = -v_PB

untuk lebih memahami jurus jitu yang pertama ini, mari kita simak beberapa contoh soal berikut.

Contoh soal 1
Sebuah pesawat bergerak dengan kecepatan 0,6 c terhadap bumi. Dari pesawat ditembakkan peluru dengan kecepatan 0,4 c searah dengan gerak pesawat. Kecepatan peluru terhadap bumi adalah ….

pembahasan soal nomor 1:

Berdasarkan soal di atas, kita dapat mengetahui ada tiga buah objek yang diamati yakni pesawat (indeks “P”), peluru (indeks “R”), dan bumi (indeks “B”), gerakan ketiga objek tersebut dapat diilustrasikan sebagai berikut.

v_PB = 0,6c (kecepatan pesawat relatif terhadap bumi)
v_RP = 0,4c (kecepatan peluru relatif terhadap pesawat)
v_RB = ... ? (kecepatan peluru relatif terhadap bumi)
tuliskan persamaan umumnya sebagai berikut

(hasil kecepatannya tidak melebihi “c”)

Contoh Soal 2
Dua buah jet F16 Hornet dan F15 Tiger saling berpapasan, pengamat dibumi mengukur kecepatan jet F16 = 0,75 c dan jet F15 = 0,85 c. Tentukan kecepatan relatif jet F15 terhadap jet F16?

pembahasan soal nomor 2:

Berdasarkan soal di atas, kita dapat mengetahui ada tiga buah objek, yakni jet F16 Hornet (indeks “H”), jet F15 Tiger (indeks “T”) dan bumi (indeks “B”), gerakan ketiga objek tersebut dapat diilustrasikan sebagai berikut.

Perhatikan pertanyaannya, yakni kecepatan relatif jet F15 (Tiger) terhadap jet F16 (Hornet) sehingga penulisan indeks kecepatannya adalah v_TH.
v_HB = 0,75c (kecepatan pesawat F16 relatif terhadap bumi)
v_BH = -0,75c (ketika indeksnya di balik, maka akan bernilai negatif)
v_TB = -0,85c (kecepatan pesawat F15 relatif terhadap bumi)
tanda negatif, karena pesawat F15 Tiger bergerak ke kiri
v_TH = ... ? (kecepatan pesawat F15 relatif terhadap pesawat F16)
kita dapat menuliskan persamaan umumnya sebagai berikut

Tanda negatif menunjukkan pesawat F15 Tiger bergerak ke arah kiri relatif terhadap bumi (hasilnya kurang dari “c”)

Contoh soal 3
Pesawat angkasa Alfa berkecepatan 0,9 c terhadap bumi, jika pesawat Beta melewati pesawat Alfa dengan kecepatan relatif 0,5 c. Berapakah kecepatan pesawat Beta terhadap bumi?

pembahasan soal nomor 3:

Berdasarkan soal kita dapat mengetahui ada tiga objek yakni pesawat angkasa Alfa (indeks “A”, pesawat angkasa Beta (indeks “B”), dan bumi (indeks “P”). gerak ketiga pesawat tersebut dapat diilustrasikan sebagai berikut.

v_AP = 0,9c (kecepatan pesawat alfa terlatif terhadap bumi)
v_BA = 0,5c (kecepatan pesawat Beta relatif terhadap pesawat Alfa)
v_BP = ... ? (kecepatan pesawat Beta relatif terhadap bumi)
kita dapat menuliskan persamaan umumnya sebagai berikut

(hasil kecepatannya tidak melebihi “c”)

Jurus Jitu Kedua : hubungan antara kecepatan “v” dengan nilai “γ”

Dalam menganalisis gerak benda dengan kecepatan yang mendekati kecepatan cahaya, kita akan mengenal suatu nilai “γ” yang merupakan “faktor koreksi” dimana besarnya kecepatan ini dapat ditentukan dari kecepatan benda "v". nilai “γ” ini akan selalu ada ketika membahas soal tentang relativitas khusus Einstein baik itu terkait dengan massa, panjang, waktu, energi maupun momentum relativistik. Secara matematis hubungan antara kecepatan benda "v" dengan nilai “γ” dapat dilihat sebagai berikut.

Ketika melihat persamaan di atas, biasanya para siswa sudah berpikiran bahwa akan rumit penyelesaiannya sehingga menyebabkan rasa tidak ingin melanjutkan mengerjakan soal tersebut. sebagai contoh untuk benda yang bergerak dengan kecepatan 0,6c, nilai “γ” dapat ditentukan seperti berikut.

cara yang panjang seperti di atas sering kali membuat siswa sudah malas untuk mengerjakan soal. Nah pada kesempatan kali ini yang ingin saya share adalah salah satu cara atau teknik yang dapat digunakan untuk menentukan nilai “γ” dari kecepatan benda atau sebaliknya yakni dengan menggunakan konsep phytagoras.
Hubungan antara nilai “γ” dan kecepatan "v" dapat terlihat pada konsep phytagoras. Perhatikan gambar berikut untuk lebih jelasnya,

Konsep phytagoras sering digambarkan dalam segitiga siku-siku seperti gambar di atas yang terdiri dari tiga sisi yakni 2 sisi siku-siku dan satu sisi miring, segitiga siku-siku memiliki persamaan tersendiri yakni c² = a² + b² dengan c adalah sisi miring serta a dan b adalah sisi siku-sikunya. misalkan sebuah benda bergerak dengan kecepatan v = 0,6c, maka kita dapat menuliskannya dalam bentuk pecahan biasa v = 6/10 c, dimana pembilang (6) sebagai salah satu sisi siku-siku dan penyebut (10) sebagai sisi miringnya (perhatikan gambar garis kuning). pasangan sisi siku-siku lainnya kita misalkan “x” seperti terlihat pada gambar. nilai “γ” dalam bentuk pecahan disusun atas sisi miring sebagai pembilang (10) dan sisi siku-siku yang belum diketahui sebagai penyebut (x) , sehingga dengan menggunakan aturan phytagoras pasangan angka untuk triple phytagoras yang cocok adalah 6, 8, 10. Dengan demikian nilai “γ” dapat dengan mudah kita ketahui besarnya 10/8.
Teknik ini dapat kita gunakan untuk menyelesaikan berbagai permasalahan terkait dengan relativitas khusus Einstein, berikut disajikan tabel hubungan antara kecepatan v dengan nilai “γ” dengan menggunakan triple phytagoras.

Untuk lebih memahami jurus jitu yang kedua ini, perhatikan beberapa contoh soal dibawah ini.

Contoh soal 1
Pada saat bergerak, panjang sebuah pesawat menjadi setengah dari pesawat itu dalam keadaan diam. Jika c adalah kecepatan cahaya, maka kecepatan pesawat itu relatif terhadap pengamat yang diam adalah ….

pembahasan soal nomor 1:

Berdasarkan soal dapat diketahui,
L = ½ L₀
v ... ?
persamaan panjang relativistik benda adalah

Jika kita setarakan dengan soal, maka

Ingat dengan menggunakan konsep tripel phytagoras sisi miringnya adalah 2 dan satu sisi siku-sikunya adalah 1, maka sisi siku-siku lainnya dapat ditentukan dengan cara
c² = a² + b²
2² = 1² + x²
4 = 1 + x²
x² = 3
x = √3 panjang sisi siku-siku lainnya (sesuai dengan tabel di atas), sehingga kecepatan yang dimiliki oleh pesawat adalah v = ½ √3 c.

Contoh soal 2
Massa benda yang bergerak dengan kecepatan 0,8 c akan berubah menjadi n kali massa diamnya, maka n adalah ….

pembahasan soal nomor 2:

Berdasarkan soal dapat diketahui
v = 0,8 c
m = n m₀
n ... ?
persamaan untuk massa relativistik adalah
m = γ m₀
jadi pada dasarnya, n adalah nilai γ.
v = 0,8 c
v = 8/10 c
dimana:
10 adalah sisi miring
8 adalah salah satu sisi siku-siku,
Besarnya sisi siku-siku lainnya ditentukan dengan cara
c² = a² + b²
10² = 8² + x²
100 = 64 + x²
x² = 36
x = 6
jadi besar n atau nilai “γ” nya adalah
γ = 10/6

Contoh soal 3
Berapakah massa relativistik sebuah partikel (massa diam = 6 kg) yang bergerak dengan kelajuan 0,28 c?

pembahasan soal nomor 3:

Berdasarkan soal dapat diketahui
m₀ = 6 kg
v = 0,28 c
m ... ?
persamaan untuk massa relativistik adalah
m = γ m₀
sehingga kita menentukan nilai γ terlebih dahulu dengan cara sebagai beriku
v = 0,28 c = 7/25 c
pasangan tripel phytagoras untuk bilangan 7 dan 25 adalah 24 (lihat di tabel), sehingga nilai γ = 25/24
jadi massa relativistiknya
m = γ m0
m = 25/24 . 6
m = 25/4
m = 6,25 kg

Contoh soal 4
Agar energi kinetik benda bernilai 20% energi diamnya dan c adalah kelajuan cahaya dalam ruang hampa, maka benda harus bergerak dengan kelajuan ....

pembahasan soal nomor 4:

Berdasarkan soal dapat diketahui
EK = 20% E₀
v... ?
persamaan untuk energi relativisitik adalah
EK = (γ – 1) E₀
20% E₀ = (γ – 1) E₀
0,2 = γ – 1
γ = 1,2
γ = 12/10
dimana
12 merupakan sisi miring
10 merupakan salah satu sisi siku-siku
Untuk itu kita dapat menentukan sisi siku-siku yang lain dengan cara
c² = a² + b²
12² = 10² + x²
144 = 100 + x²
x² = 44
x = 2√11
sehingga benda harus bergerak dengan kecepatan

Demikian jurus jitu : menyelesaikan soal relativitas khusus Einstein yang bisa saya bagikan pada kesempatan kali ini, semoga bisa memberikan manfaat bagi para pembaca. jika ada saran-saran, kritik bisa dituliskan di kolom komentas

GALLERY

Iseng-iseng buat desain yang terinspirasi dari konsep-konsep materi pelajaran, seperti konsep fisika, kimia, biologi, dll. Disini karena saya tidak mempunyai tukang sablon maka desain-desain tersebut

Adwood Machine (Image)

Physics Equation

Simple Pendulum

Free Fall Motion

Density is Love

Newton Second’ law (T1)

DNA

Phi Number

Prinsip Aufbau

Saya mengupload gambar-gambar tersebut di situs POD (Print On Demand), karena saya tidak memiliki tukang sablon. jadi untuk urusan produksi akan di tangani oleh situs tersebut. berikut link toko saya di situs tersebut :

Ciptaloka : Lshirt

TeePublic : hakim91

Induksi Elektromagnetik | Soal dan Pembahasan (Fisika Kelas 12 - part 1)

Induksi elektromagnetik merupakan salah satu materi yang ada di kelas 12 semester 1, materi ini sebenarnya tidak terlalu sulit untuk dipahami karena berkaitan dengan kehidupan sehari – hari sehingga dapat diilustrasikan. Untuk materi induksi elektromagnetik nanti akan saya tulis, ditunggu ya. Pada kesempatan kali ini saya akan membahas beberapa soal tentang induksi elektromagnetik yang disertai dengan pembahasan dan tips untuk mengerjakan soal. Soal latihan ini saya tulis menjadi 2 bagian dan ini adalah soal dan pembahasan induksi elektromagnetik bagian 1, selamat menikmati.

Soal nomor 1

Sebuah bidang limas dengan, yang ukuran rusuk seperti tampak pada gambar berikut. Diletakkan dalam suatu medan magnet homogen.

Besar induksi magnetik 0,25 T dan berarah ke sumbu Y+. Fluks magnetik melalui sisi PQRS adalah ....
A. 0,10 Wb
B. 0,12 Wb
C. 0,15 Wb
D. 0,50 Wb
E. 0,60 Wb
Kunci jawaban: "B"

pembahasan soal nomor 1:

Berdasarkan soal dapat diketahui
B = 0,25 T
A = 1,6 x 0,5 = 0,8 m²
Untuk mempermudah mengerjakan perhatikan gambar berikut

Berdasarkan gambar di atas, kita dapat mengetahui bahwa sudut yang dibentuk oleh medan magnet dengan garis normal sebesar α, dengan nilai cos α = 0,3/0,5 = 0,6. Sehingga secara matematis kita dapat menuliskan besar fluks magnetiknya sebesar
Φ = B . A . cos α
Φ = 0,25 . 0,8 . 0,6
Φ = 0,12 Wb

Soal nomor 2

perhatikan gambar berikut!

Suatu batang logam netral bergerak dengan kecepatan v ke kiri melewati daerah bermedan magnetik seragam B dengan arah keluar bidang kertas. Gambar yang paling tepat melukiskan distribusi muatan pada permukaan batang logam adalah

Kunci jawaban: "D"

pembahasan soal nomor 2:

Berlaku kaidah tangan kanan dengan aturan
Ibu jari sebagai arah kecepatan “v”
Jari telunjuk sebagai arah medan magnet “B”
Jari tengah sebagai arah arus listrik “i” Sehingga pada batang logam akan mengalir arus dari bawah ke atas, maka bagian bawah batang potensialnya lebih tinggi (+) dan bagian atas logam potensialnya lebih rendah (-)

Soal nomor 3

Sebuah pesawat terbang kecil dengan panjang sayap 10 m, terbang secara mendatar ke arah utara pada kelajuan 60 m/s dalam suatu daerah dengan medan magnetik bumi 50 μT berarah 60⁰ ke bawah terhadap arah mendatar (tanah). Besar GGL induksi antara ujung-ujung sayap adalah ....
A. 50 mV
B. 44 mV
C. 37 mV
D. 31 mV
E. 26 mV
Kunci jawaban: "E"

pembahasan soal nomor 3:

Berdasarkan soal dapat diketahui
l = 10 m
v = 60 m/s
B = 50 μT = 50 x 10^-6 T
θ = 60⁰
ε ... ?
untuk menyelesaikan soal di atas kita dapat menggunakan persamaan
ε = B l v sin θ
ε = 50 x 10^-6 . 10 . 60 . sin 60⁰
ε = 3 x 10^-2 . 0,87
ε = 2,61 x 10^-2 V
ε = 0,26 mV

Soal nomor 4

Perhatikan hal-hal berikut    
1) Menjaga suatu arus stabil pada kumparan lain yang posisinya tetap dengan kumparan A
2) Memutuskan arus dalam kumparan lainnya yang posisinya tetap di dekat kumparan A
3) Dengan cepat menggerakkan sebuah magnet ke dalam kumparan A
4) Dengan cepat menggerakkan sebuah magnet ke dalam dan keluar kumparan A
Saat terjadi secara terpisah, yang dapat menghasilkan GGL induksi pada kumparan A dengan posisi tetap ditunjukkan oleh nomor ....
A. 1)
B. 3)
C. 1) dan 3)
D. 2), 3), dan 4)
E. 1), 2), 3) dan 4)
Kunci jawaban: "D"

pembahasan soal nomor 4:

Secara proses timbulnya GGL induksi dapat digambarkan sebagai berikut
Perubahan medan magnet → perubahan fluks magnet → GGL Induksi
Perubahan medan magnet dapat terjadi dengan dua cara

1. Menggerakkan kumparan di sekitar magnet atau sebaliknya (ada kecepatan)
2. Mengubah besarnya arus listrik (bisa menggunakan arus AC atau memutus hubungkan dengan sumber arus)

Berdasarkan penjelasan di atas, maka yang dapat menghasilkan GGL induksi pada kumparan A adalah pernyataan nomor 2), 3) dan 4)

Soal nomor 5

Pada gambar berikut, kumparan 1 sedang digerakkan menuju kumparan 2.

Perhatikan pernyataan-pernyataan berikut.
1) Kelajuan kumparan 1 ditingkatkan
2) Banyak lilitan kumparan 1 ditingkatkan
3) Baterai yang dihubungkan ke kumparan 1 diganti dengan baterai yang GGL-nya lebih tinggi
4) Hambatan ditambah

Perubahan yang akan meningkatkan arus induksi dalam kumparan 2 ditunjukkan oleh pernyataan nomor....
A. 4)
B. 1) dan 4)
C. 2) dan 3)
D. 1), 2), dan 3)
E. 1), 2), 3), dan 4)
Kunci jawaban: "D"

pembahasan soal nomor 5:

Proses timbulnya arus listrik induksi dapat digambarkan sebagai berikut
Perubahan medan magnet → perubahan fluks magnet → GGL Induksi → arus induksi
Peningkatan arus induksi dapat terjadi jika GGL induksinya juga meningkat, sesuai dengan persamaan
ε = NBAω
sehingga GGL induksi sebanding dengan
N = jumlah lilitan
B = medan magnet
A = Luas penampang
ω = kecepatan sudut

maka untuk meningkatkan arus induksi (meningkatkan GGL induksi) sesuai dengan pernyataan 1), 2), dan 3)

Soal nomor 6

Suatu medan magnetik seragam B yang tegak lurus bidang kertas melewati loop, seperti ditunjukkan gambar di samping. Medan magnetik berada dalam suatu jari-jari a dengan a < b dan berubah pada laju tetap. jika GGL induksi dalam loop kawat jari-jari b adalah ε, GGL induksi dalam loop kawat jari-jari 2b adalah ....

A. Nol
B. ε/2
C. ε
D. 2ε
E. 4ε
Kunci jawaban: "E"

pembahasan soal nomor 6:

Berdasarkan soal dapat diketahui
r₁ = b
r₂ = 2b
ε₁ = ε
ε₂ ... ?
berdasarkan persamaan
ε = NBAω
kita dapat mengetahui bahwa GGL induksi sebanding dengan luas penampang, sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut

Soal nomor 7

Dua kumparan P dan Q dililitkan pada suatu inti besi lunak seperti ditunjukkan pada gambar. sakelar K mula-mula terbuka dan kemudian tertutup

Pernyataan yang benar mengenai rangkaian dengan kumparan Q setelah sakelar K ditutup adalah ....
A. Arus akan mengalir sesaat dari X ke Y melalui G
B. Arus akan mengalir sesaat dari Y ke X melalui G
C. Arus tetap akan mengalir sesaat dari X ke Y melalui G
D. Arus tetap akan mengalir sesaat dari Y ke X melalui G
E. Tidak akan ada arus mengalir di G
Kunci jawaban: "B"

pembahasan soal nomor 7:

Ketika sakelar K ditutup, maka arah arus dan induksi yang terjadi dapat digambarkan sebagai berikut

Untuk menentukan arah fluks (utama dan induksi) dan arah arus induksi dapat menggunakan kaidah tangan kanan, dimana

1. 4 jari melingkar sebagai arah arus
2. Ibu jari menunjukkan arah fluks magnetnya

Sehingga arus akan mengalir pada galvanometer, tapi ingat fluks utama hanya akan muncul jika ada perubahan arus listrik (ketika sakelar ditutup) jika kemudian sakelar dibiarkan tertutup maka tidak ada arus fluks utama yang muncul sehingga tidak ada fluks induksi dan arus listrik induksi. oleh sebab itu arus induksi hanya muncul sesaat saja.

Soal nomor 8

Sebuah solenoide dengan 200 lilitan dan luas penampang 0,7 cm² memiliki medan magnetik 0,80 T sepanjang porosnya. Jika medan magnetik dikurung dalam solenoide dan berubah pada laju 0,30 T/s. besar beda potensial dalam solenoida akan menjadi adalah ....
A. 0,18 V
B. 0,24 V
C. 0,48 V
D. 4,8 V
E. 7,2 V
Kunci jawaban: "D"

pembahasan soal nomor 8:

Berdasarkan soal dapat diketahui
N = 200 lilitan
A = 0,7 cm² = 7 x 10-5 m²
dB/dt = 0,30 T/s
ε ... ?

Soal nomor 9

Sebuah loop bidang terdiri atas empat lilitan kawat, masing-masing luasnya 300 cm2. Diarahkan tegak lurus suatu daerah medan magnetik yang besarnya bertambah secara tetap dari 10 mT menjadi 25 mT dalam waktu 5 ms. Arus induksi yang dibangkitkan dalam kumparan sebesar 72 mA, jika hambatan kumparan adalah ....
A. 5 Ω
B. 7,5 Ω
C. 10 Ω
D. 12,5 Ω
E. 15 Ω
Kunci jawaban: "A"

pembahasan soal nomor 9:

Berdasarkan soal dapat diketahui
A = 300 cm² = 3 x 10^-2 m²
N = 4
ΔB = 25 – 10
ΔB = 15 mT = 15 x 10^-3 T
Δt = 5 ms = 5 x 10^-3 s
I = 72 mA = 72 x 10^-3 A
R ... ?
Menentukan GGL Induksi
ε = NA ΔB/Δt
ε = 4 . 3 x 10^-2 (15 x 10^-3 / 5 x 10^-3)
ε = 36 x 10^-2 V
Menentukan nilai hambatan
R = ε/I
R = 36 x 10^-2 / 72 x 10^-3
R = 5 Ω

Soal nomor 10

Sebuah kawat melingkar dengan hambatan 9 Ω diletakkan dalam fluks magnetik yang berubah terhadap waktu, dinyatakan dengan Φ = (3t – 5)² . arus yang mengalir dalam kawat pada t = 4 s adalah ....
A. 4,7 A
B. 8 A
C. 18 A
D. 30 A
E. 42 A
Kunci jawaban: "A"

pembahasan soal nomor 10:

Berdasarkan soal dapat diketahui
N = 1
R = 9 Ω
Φ = (3t – 5)²
t = 4 s
I ... ?
Menentukan GGL Induksi

Menentukan arus induksi
R = ε/I
R = 42/9
R = 4,7 Ω

Soal nomor 11

Sebuah kumparan mempunyai induktansi 700 mH. besara GGL induksi yang dibangkitkan dalam kumparan itu jika ada perubahan arus listrik dari 300 mA menjadi 60 mA dalam waktu 0,02 sekon secara beraturan adalah ....
A. 2,8 V
B. 4,2 V
C. 4,8 V
D. 6,4 V
E. 8,4 V
Kunci jawaban: "E"

pembahasan soal nomor 11:

Berdasarkan soal dapat diketahui
L = 700 mH = 7 x 10^-1 H
Δi = 300 – 60
Δi = 240 mA = 24 x 10^-2 A
Δt = 0,02 s = 2 x 10^-2 s
ε ... ?
ε = L Δi/Δt
ε = 7 x 10^-1 (24 x 10^-2 / 2 x 10^-2)
ε = 7 x 10^-1 . 12
ε = 8,4 V

Soal nomor 12

Pada sebuah kumparan mengalir arus dengan persamaan I = sin πt. Jika koefisien induksi diri kumparan 8 H. GGL induksi dari yang terjadi dalam kumparan tersebut sesudah selang waktu 1/3 detik adalah ....
A. ¼π volt
B. 1/5π volt
C. ½π volt
D. 2π volt
E. 4π volt
Kunci jawaban: "E"

pembahasan soal nomor 12:

Berdasarkan soal dapat diketahui
I = sin πt
L = 8 H
t = 1/3 s
ε ... ?

Soal nomor 13

Sebuah generator menghasilkan GGL maksimum 12 V ketika kumparan berputar pada 750 rpm (rpm = rotasi per menit). GGL maksimum generator ketika kumparan berputar 2.250 rpm adalah ....
A. 4 V
B. 12 V
C. 18 V
D. 27 V
E. 36 V
Kunci jawaban: "E"

pembahasan soal nomor 13:

Berdasarkan soal dapat diketahui
ε₁ = 12 V
ω₁ = 750 rpm
ω₂ = 2.250 rpm
ε₂ ... ?
hubungan antara GGL induksi dengan kecepatan sudut dapat terlihat pada persamaan ini
ε = NBAω
berdasarkan persamaan di atas, kita dapat mengetahui bahwa GGL induksi sebanding dengan kecepatan sudut, sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut

Soal nomor 14

Sebuah trafo step-up mengubah tegangan 20 V menjadi 160 V. jika efisiensi trafo itu 75% dan kumparan sekundernya dihubungkan ke lampu 160 V, 60 W, kuat arus dalam kumparan primernya adalah ....
A. 8 A
B. 6 A
C. 4 A
D. 3 A
E. 2 A
Kunci jawaban: "C"

pembahasan soal nomor 14:

Berdasarkan soal kita dapat mengetahui
V_P = 20 V
V_S = 160 V
η = 75%
V_L = 160 V
P_L = 60 W
I_P ... ?
Jika kita melihat spesifikasi lampu, maka tegangan sekunder yang dikeluarkan oleh trafo sesuai untuk menyalakan lampu dengan optimal dengan kuat arus yang mengalir pada lampu adalah
P = V . I
60 = 160 . I
3/8 A = I
Arus yang mengalir pada lampu tersebut sama dengan arus sekunder yang dihasilkan oleh trafo. Sehingga kita dapat menentukan besar arus primernya dengan persamaan

Soal nomor 15

Sepuluh lampu 12 V/20 W terhubung paralel dengan kumparan sekunder suatu trafo step-down dengan kumparan primernya terhubung dengan sumber daya PLN 200 V. jika besar arus primer yang dapat diambil dari sumber daya PLN adalah 5/4 A, besar efisiensi trafo itu adalah ....
A. 30 %
B. 50 %
C. 75 %
D. 80 %
E. 90 %
Kunci jawaban: "D"

pembahasan soal nomor 15:

Berdasarkan soal kita dapat mengetahui
n = 10 buah
V_L = 12 V
P_L = 20 W
V_P = 200 V
I_P = 5/4 A
η ... ?
kita anggap bahwa semua lampu bekerja dengan optimal
Tegangan yang diterima oleh lampu sama dengan tegangan sekunder trafo yakni
V_S = 12 V
Setiap lampu akan mendapat tegangan 12 V dengan kuat arus yang mengalir di lampu adalah
P_L = V_L . I_L
20 = 12 . I_L
5/3 A = I_L
Untuk 10 buah lampu sejenis yang dirangkai paralel, besar kuat arus total dalam rangkaian adalah
I_tot = 5/3 . 10
I_tot = 50/3 A
Besar arus total ini sama dengan besar arus yang dihasilkan oleh trafo atau arus sekundernya. Efisiensi trafo dapat ditentukan dengan persamaan

Hukum Hooke | Materi fisika kelas 11

Sebuah pegas ketika diberikan gaya (ditarik atau ditekan) akan kembali ke keadaan awal sesaat setelah gaya tersebut dihilangkan, hal yang sama juga berlaku untuk benda – benda yang bersifat elastis dan keadaan ini berlaku selama masih pada daerah elastis. Berdasarkan fenomena ini pada tahun 1976, seorang fisikawan bernama Robert Hooke mengemukakan hukum Hooke yang menyatakan bahwa “besarnya gaya yang diperlukan untuk meregangkan atau merapatkan sebuah pegas (gaya pegas) sama besar dengan besarnya gaya yang digunakan untuk meregangkan atau merapatkan pegas tersebut sejaub x”. Secara matematis hukum Hooke dapat ditulis

Keterangan :
F_p = gaya pegas (N)
k = Konstanta pegas (N/m)
x = perubahan panjang pegas (m)

konstanta pegas merupakan suatu nilai yang bergantung dari jenis pegas yang digunakan, konstanta pegas ini berbanding terbalik dengan perubahan panjang pegas secara matematis dapat dijelaskan bahwa semakin besar konstanta pegas berbanding terbalik dengan perubahan panjang pegas. Hal ini juga mengandung makna bahwa semakin besar konstanta pegas maka benda semakin susah untuk berubah panjangnya atau dibutuhkan gaya yang lebih besar ketika ingin mengubah panjang pegas atau dapat pula dikatakan bahwa pegas tersebut semakin bersifat tidak elastis.
Tanda negatif menunjukkan bahwa gaya pegas arahnya selalu berlawanan dengan arah perpindahannya dari titik kesetimbangan, gaya pegas juga berfungsi untuk memulihkan panjang pegas kembali ke bentuk semula, oleh karena itu gaya pegas sering juga disebut dengan gaya pemulih.
Penting
Beberapa buku menuliskan rumus di atas tanpa tanda negatif (F = kΔx), hal ini dikarenakan gaya yang dimaksud pada persamaan tersebut bukan gaya pegas akan tetapi gaya luar yang dikerjakan pada pegas tersebut. Antara gaya pegas dan gaya luar yang dikerjakan ini memang besarnya sama akan tetapi arahnya berlawanan jadi jangan sampai bingung ketika melihat kedua rumus tersebut.

Gambar 6. Ilustrasi gaya pegas atau gaya pemulih
(sumber: Principle of Physics)

Perhatikan sebuah benda yang terhubung dengan sebuah pegas dengan salah satu ujungnya menempel di tembok, ketika balok bergerak ke kanan (x < 0) dan menarik pegas (gambar 6a) sehingga pegas menjadi lebih panjang maka arah gaya pegas akan ke kiri. Ketika balok berada pada titik kesetimbangan (gambar 6b) gaya pegas bernilai nol (x = 0), dan ketika balok bergerak ke kiri (x < 0) menekan pegas (gambar 6c) sehingga pegas menjadi lebih pendek maka gaya pegas memiliki arah ke kanan. Sehingga dari hasil mengamati gambar tersebut kita mengetahui bahwa gaya pegas berfungsi untuk mengembalikan pegas ke posisi awalnya atau posisi kesetimbangan. Hubungan antara gaya pegas dan perubahan panjang dapat pula dilihat dari grafik di bawah ini.

Gambar 7. (a) grafik hubungan antara gaya pegas dengan perubahan panjang pegas, (b) grafik hubungan antara gaya F dengan perubahan panjang pegas, (s) grafik hubungan antara gaya F dengan perubahan panjang pegas untuk beberapa pegas

Perhatikan gambar di atas, gambar 7a menunjukkan hubungan antara gaya pegas dengan perubahan panjang pegas, ketika perubahan panjang pegas bernilai negatif (x < 0 ) maka gaya pegas bernilai positif (F_p > 0) sedangkan ketika perubahan panjang pegas bernilai positif (x > 0) maka gaya pegas bernilai negatif (F_p < 0), nilai perubahan panjang pegas berlawanan dengan nilai gaya pegas hal ini sesuai dengan persamaan di atas dengan tanda minus (-). Gambar 7b sedikit berbeda dengan gambar 7a yakni terletak gaya yang digambarkan, pada grafik 7a gaya yang digambarkan dalam grafik merupakan gaya pegas (gaya pemulih) sedangkan pada grafik 7b gaya yang digambarkan dalam grafik merupakan gaya yang dikerjakan pada pegas yang sesuai dengan persamaan F = kx (tanpa tanda minus) sehingga terlihat bahwa gaya sebanding dengan perubahan panjang pegas, semakin besar gaya yang bekerja maka semakin besar pula perubahan panjang pegasnya. Jika kita analisis lebih lanjut grafik pada gambar 7b merupakan grafik berbentuk garis lurus (linier) yang mana secara matematis memiliki persamaan umum y = mx dimana m merupakan gradien dari grafik tersebut, apabila kita hubungkan antara persamaan garis lurus ini dengan persamaan hukum hooke maka
y = mx → F = kx
kedua persamaan di atas menunjukkan adanya kesesuaian dimana gaya F dianalogikan sebagai sumbu y, perubahan panjang pegas x dianalogikan sebagai sumbu x dan konstanta pegas k dianalogikan sebagai gradien grafik m. Grafik 7c menunjukkan grafik hubungan antara gaya yang bekerja dengan perubahan panjang untuk empat buah pegas, terlihat bahwa perbedaan dari semua grafik tersebut terletak pada kemiringannya (atau gradien), sehingga dengan menggunakan analisis gradien seperti di atas kita dapat mengatakan bahwa semakin curam grafiknya (gradiennya semakin besar) maka nilai konstanta pegasnya juga semakin besar yang artinya pegas tersebut semakin tidak elastis, begitu pula sebaliknya semakin landai grafiknya (gradien semakin kecil) maka nilai konstanta pegasnya semakin kecil yang artinya pegas tersebut semakin bersifat elastis. Jadi jika diurutkan berdasarkan nilai konstanta pegasnya dari terbesar ke terkecil maka k₁ > k₂ > k₃ > k₄.

Hubungan antara hukum Hooke dengan Modulus Young

Pada dasarnya baik hukum Hooke dan modulus Young sama-sama berkaitan dengan sifat elastisitas benda, tetapan pegas k berlaku untuk benda – benda elastis yang masih di daerah elastisnya (perhatikan kembali grafik hubungan antara tegangan dan regangan). persamaan hukum Hooke dan persamaan modulus Young memiliki hubungan yang saling berkaitan, jika kita telaah kembali persamaan pada modulus Young dapat kita tulis

Berdasarkan kedua persamaan di atas, maka kita dapat menuliskan persamaan untuk konstanta pegas adalah sebagai berikut

Keterangan :
k = konstanta pegas (N/m)
L = panjang benda (m)
E = Modulus Young (N/m²)
A = luas penampang (m²)
(luas penampang umumnya A = πr² , dimana r adalah jari-jari)

Hukum Hooke pada susunan pegas

Susunan pegas seri

Susunan pegas seri tampak seperti di atas dimana dua buah pegas yang masing-masing memiliki konstanta pegas k₁ dan k₂ disusun secara memanjang dengan satu sisinya saling bartauan (gambar kiri) memiliki konstanta yang identik dengan sebuah pegas dengan konstanta pegas sebesar ks (nilai ini disebut dengan konstanta pengganti), karakteristik dari pegas yang dirangkai secara seri adalah

1. Gaya total yang bekerja pada sistem sama dengan Gaya yang bekerja pada masing – masing pegas
F_tot = F₁ = F₂ = ... = F_n
2. Pertambahan panjang total sistem pegas adalah hasil penjumlahan pertambahan panjang masing – masing pegas
x_tot = x₁ + x₂ + ... + x_n
3. Konstanta pengganti susunan seri pegas (k_s) dapat ditentukan dengan cara

khusus dua pegas identik yang dirangkai seri untuk menentukan konstanta penggantinya, persamaan di atas dapat ditulis

khusus untuk "n" buah pegas identik dirangkai seri, dalam menentukan konstanta penggantinya persamaan di atas dapat ditulis

Dimana “n” adalah jumlah pegas yang dirangkai seri

Susunan pegas paralel

Susunan pegas paralel tampak seperti di atas dimana dua buah pegas yang masing-masing memiliki konstanta pegas k₁ dan k₂ disusun secara sejajar dengan kedua sisinya saling bartauan (gambar kiri) memiliki konstanta yang identik dengan sebuah pegas dengan konstanta pegas sebesar kp (nilai ini disebut dengan konstanta pengganti), karakteristik dari pegas yang dirangkai secara paralel adalah

1. gaya total yang bekerja pada sistem merupakan hasil penjumlahan dari gaya yang bekerja pada masing – masing pegas
F_tot = F₁ + F₂ + ... + F_n
2. pertambahan panjang pegas total sistem sama dengan pertambahan panjang masing – masing pegas
x_tot = x₁ = x₂ = ... = x_n
3. Konstanta pengganti susunan paralel pegas (k_p) dapat ditentukan dengan cara

Khusus untuk "n" buah pegas identik disusun paralel maka untuk menentukan konstanta pegas penggantinya persamaan di atas dapat ditulis

Dengan “n” sama dengan jumlah pegas yang disusun paralel

Penting

Perhatikan kembali karakteristik antara susunan pegas secara seri dan paralel ternyata memiliki karakteristik yang saling berlawanan, jika pada susunan pegas seri gaya totalnya sama dengan gaya pada masing – masing pegas, maka pada susunan pegas paralel pertambahan panjang pegas totalnya yang sama dengan pertambahan panjang pada masing – masing pegas. Untuk lebih memahami materi ini silahkan dilihat latihan soal tentang elastisitas

Elastisitas | Materi Fisika Kelas 11

ketika kita menarik karet atau melihat pegas yang ditekan, keduanya akan kembali ke bentuk semula ketika tarikan pada karet dilepaskan atau tekanan pada pegas dilepaskan. Kemampuan suatu benda untuk kembali ke bentuk awalnya segera setelah gaya luar yang diberikan dihilangkan disebut dengan elastisitas atau sifat elastis bendanya disebut dengan benda elastis. Semakin elastis suatu benda maka kecepatan benda tersebut kembali ke bentuk semula akan semakin cepat, akan tetapi pada kondisi tertentu benda – benda tersebut tidak mampu kembali ke bentuknya meskipun gaya luar yang dikerjakan sudah dihilangkan.

Berbeda dengan pada karet atau pegas, jika kita memberikan gaya kepada plastisin, maka plastisin tidak dapat segera kembali ke bentuk semula. Benda – benda yang seperti ini disebut dengan benda tidak elastis atau benda plastis. Baik benda elastis maupun benda plastis sama – sama memiliki fungsi dan kegunaan tersendiri, Pada kesempatan kali ini kita akan membahas tentang elastisitas suatu benda, faktor – faktor yang mempengaruhinya, kapan benda tersebut tidak dapat kembali ke bentuk semula (tidak elastis lagi). Untuk itu silahkan melanjutkan pembahasan singkat di bawah ini.

Analisis DImensi | Materi Fisika kelas 10

Analisis Dimensi

Seperti yang telah dijelaskan pada bagian besaran dan satuan sebelumnya, bahwa besaran turunan memiliki lebih dari satu satuan yang terbentuk dari dua atau lebih besaran pokok. Satuan – satuan ini menunjukkan faktor penyusun dari suatu besaran turunan tersebut, permasalahannya adalah terkadang satuan yang digunakan di suatu negara tidak sama dengan negara lain sehingga diperlukan sebuah acuan standar untuk mengetahui faktor-faktor dari penyusun suatu besaran turunan. Berdasarkan hal tersebut dibuatlah sebuah cara untuk melihat faktor – faktor untuk menyatakan suatu besaran turunan yang disebut Dimensi. Jadi dengan analisis dimensi kita bisa langsung mengetahui kombinasi besaran-besaran pokok yang menyusun besaran turunan. Dalam penulisan dimensi suatu besaran X misalnya, kita harus meletakkannya di dalam tanda kurung persegi seperti berikut [X]. Dimensi untuk ketujuh besaran pokok dapat dilihat pada tabel berikut

Tabel 5. Dimensi besaran-besaran pokok