Salah satu materi
fisika kelas 12 di semester 1 adalah rangkaian seri RLC pada arus bolak-balik. Banyak
siswa yang merasa kesulitan ketika belajar materi fisika satu ini, oleh karena
ini disini saya mencoba membantu memberikan penjelasan tentang rangkaian seri
RLC pada arus bolak balik. Materi ini saya tulis sesuai dengan apa yang saya
pahami dan dengan gaya penulisan seperti ini. Selamat menikmati
Tegangan dan arus bolak-balik (AC)
Arus bolak balik atau alternating
current (AC) merupakan arus listrik yang paling banyak digunakan dalam
kehidupan sehari-hari. Listrik yang digunakan di rumah-rumah menggunakan arus
AC hal ini dikarenakan arus AC lebih mudah dihasilkan daripada arus searah atau
direct current (DC) selain itu besar tegangannya dapat diubah-ubah
dengan menggunakan transformator serta lebih cocok untuk transmisi jarak jauh
karena dapat meminimalisir kehilangan energi saat dalam perjalanan.
Arus bolak-balik dihasilkan dari generator AC
yang menggunakan cincin logam seperti digambarkan berikut ini
Gambar 1.
Generator AC
(sumber :
fundamentals of physics)
Prinsip kerja dari
generator ini pada dasarnya menggunakan hukum Faraday dan penggunaan cincin
logam (slip rings) pada generator AC memiliki fungsi sebagai pembalik
arus pada kumparan, jadi setiap setengah putaran kumparan arus induksi pada
kumparan berbalik arah sehingga menghasilkan arus bolak-balik. Agar lebih
memahami prinsip kerja dari generator AC silahkan dilihat animasi generator AC
Arus dan tegangan yang dihasilkan oleh generator
akan berubah terus terhadap waktu dan membentuk gelombang sinusiodal seperti
gambar di bawah ini.
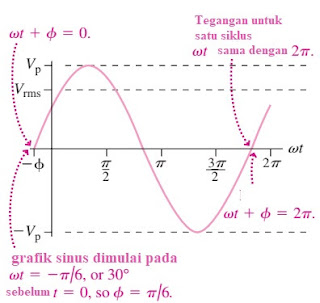
Gambar 2.
Grafik tegangan pada arus bolak balik terhadap waktu
(sumber : essential university physics)
Jika pengamatan dilakukan pada saat t=0 maka tidak ada sudut fase awal, sehingga persamaan di atas dapat ditulis
Fase diagram tegangan
dan arus bolak-balik dapat berbeda bergantung pada komponen rangkaian yang
dipasang. Hal ini akan kita bahas lebih lanjut pada rangkaian arus AC.
Tegangan efektif (Vrms) dan arus efektif (irms) pada arus bolak balik (AC)
Berdasarkan grafik
tegangan dan arus bolak-balik di atas, kita tidak dapat menentukan nilai
rata-ratanya karena akan selalu bernilai nol. Oleh karena itu dikenal istilah tegangan
efektif dan arus efektif yakni cara yang digunakan untuk menentukan besar dari
suatu besaran yang dapat bernilai positif dan negatif. Dalam menentukan nilai
efektif dari tegangan dan arus dilakukan dengan cara mengkuadratkan (square)
nilainya sehingga semua bernilai positif, menentukan nilai rata-ratanya (mean)
dan terakhir mengkakarkan nilainya (root). Cara ini biasa disebut
dengan root mean square (rms). Tegangan efektif dan arus efektif
merupakan tegangan dan arus yang terukur dalam alat ukur listrik.
Penurunan rumus arus efektif (irms)
adalah sebagai berikut:
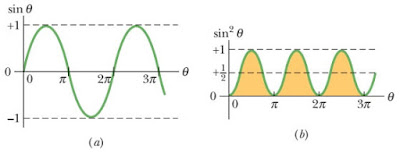
Gambar 3.
Grafik kuat arus effektif (a) grafik sinusoidal i terhadap θ = ωt; nilai
rata-rata arus i sama dengan nol dalam satu siklus luas bagian positif
sama dengan luas bagian negatif, (b) grafik kuadrat arus i2 terhadap
θ; nilai rata-rata untuk satu siklus adalah ½
(sumber : fundamentals
of physics)
Nilai cos 2θ sama dengan nol, karena setengahnya bernilai positif dan setengahnya lagi bernilai negatif. sehingga
Dengan cara yang sama didapatkan tegangan efektif untuk arus bolak balik adalah
Daya rangkaian arus bolak balik (AC)
Setiap rangkaian
listrik tidak semua energi listrik berubah menjadi energi yang lain, akan
tetapi terjadi kebocoran sehingga sebagian energi listrik hilang menjadi energi
panas. Energi yang hilang ini dalam waktu tertentu (daya yang hilang) disebut
dengan daya disipasi. Daya disipasi dapat ditentukan dengan persamaan
P = Vrms Irms → (hukum Ohm : Vrms = Irms . R)Perhatikan bahwa arus yang digunakan adalah arus efektif bukan arus maksimum
alat ukur arus listrik bolak balik (AC) : Osiloskop
Osiloskop merupakan alat ukur elektronika yang berfungsi
memproyeksikan bentuk sinyal (sinyal sinusoidal, kotak, atau gergaji) listrik
agar dapat dilihat dan dipelajari, Osiloskop biasanya digunakan untuk mengamati
bentuk gelombang yang tepat dari sinyal listrik. Selain amplitudo sinyal,
osiloskop dapat menunjukkan distorsi, waktu antara dua peristiwa (seperti lebar
pulsa, periode, atau waktu naik) dan waktu relatif dari dua sinyal terkait.
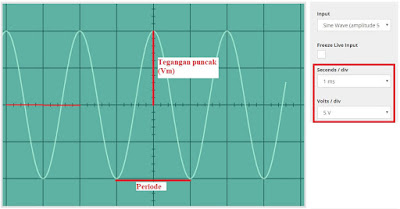
Berikut gambar hasil proyeksi osiloskop
Gambar 4.
Proyeksi sinyal sinusoidal menggunakan osiloskop
Dalam menentukan hasil
pengukuran menggunakan osiloskop perlu diperhatikan skala V/div untuk arah vertikal
dan skala t/div untuk skala horizontal (ada juga yang menggunakan V/cm dan t/ms).
Pada gambar di atas digunakan
V/div sebesar 5 V yang
artinya untuk satu kotak vertikal nilainya 5 V
t/div sebesar 1 ms yang
artinya untuk satu kotak horizontal nilainya 1 ms
pembacaan tegangan
tegangan puncak (Vm) dapat
dilihat jumlah kotak dari titik tengah ke puncak gelombang dikali dengan V/div
Vm = 2 x 5 = 10 V
pembacaan frekuensi
frekuensi dapat
ditentukan dengan mencari periode dari hasil osiloskop. Periode dinyatakan
dalam jumlah kotak arah horizontal untuk satu gelombang dikali dengan t/div
T = 2 x 1 = 2 ms = 2 .
10-3 s
Sehingga frekuensi
sinyalnya adalah
f = 1/T = 2/10-3
= 500 Hz
simulasi osiloskop di
atas dapat dilihat pada web disini
Diagram fasor pada arus listrik bolak balik (AC)
Fasor merupakan suatu vektor yang berotasi berlawanan arah jarum jam dengan kecepatan sudut yang konstan dan grafik yang menggambarkan fasor ini disebut dengan diagram fasor. Dalam kaitannya dengan arus bolak balik panjang diagram fasor menggambarkan besar tegangan, kuat arus maupun hambatan. Perhatikan contoh diagram fasor pada rangkaian resistor berikut ini
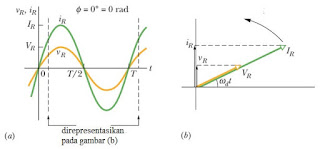
Gambar 5.
(a) grafik kuat arus dan tegangan pada resistor terhadap waktu, (b) diagram
fasor berdasarkan grafik (a).
(sumber :
fundamentals of physics)
Beberapa hal yang perlu
diperhatikan pada diagram fasor adalah
Kecepatan sudut: pada diagram fasor kecepatan sudut digambarkan berotasi
berlawanan arah dengan jarum jam.
Panjang: panjang diagram fasor menggambarkan amplitudo gelombang
sinusoida dalam hal ini adalah tegangan maksimum (Vm) dan
arus maksimum (im).
Proyeksi: proyeksi diagram fasor terhadap sumbu y merepresentasikan
nilai tegangan dan kuat arus bolak balik pada saat t .
Sudut rotasi: sudut rotasi pada diagram fasor sama dengan fase tegangan
dan kuat arus listrik bolak balik pada saat t.
Untuk diingat
Pada dasarnya fasor
bukan merupakan besaran fisika yang memiliki arah seperti gaya, kecepatan, atau
medan listrik. Diagram fasor digunakan untuk membantu menganalisis suatu
besaran fisika yang berubah secara sinusoidal terhadap waktu.
Rangkaian arus bolak balik (AC)
Berbeda dengan
rangkaian arus DC yang terdiri sumber arus searah (baterai) dan resistor, pada
rangkaian arus AC ada beberapa komponen yang dianalisis yakni resistor (R),
Induktor (L), dan kapasitor (C). Mari kita analisis satu persatu rangkaian AC
tersebut, akan tetapi perlu diperhatikan beberapa hal yakni
Tegangan dan arus
listrik bolak balik dinyatakan dalam persamaan
V = Vm sin
ωt
I = Im sin
ωt
Tegangan dan arus listrik dapat berbeda fase (Φ) bergantung pada komponen dalam rangkaian tersebut. Sumber
arus AC berbeda dengan sumber arus DC yang digambarkan sebagai berikut.
Gambar 6.
Simbol arus AC
(sumber: physics
university)
Rangkaian resistor pada arus bolak balik (AC)
Rangkaian resistor (R) murni dapat juga disebut dengan rangkaian resisif yang terdiri dari sumber arus bolak balik dan sebuah resistor seperti digambarkan sebagai berikut:
Gambar 7.
Rangkaian resistor murni
(sumber:
physics university)
Kuat arus yang mengalir
pada resistor adalah
I = Im sin
ωt
Berdasarkan hukum Ohm
(V = IR), maka tegangan pada resistor adalah
V = Vm sin
ωt
Berdasarkan persamaan di atas maka dapat kita
ketahui bahwa tidak ada perbedaan fase antara tegangan dan kuat arus listrik,
hal ini juga dapat dilihat pada grafik dan diagram fasornya sebagai berikut:
Gambar 8. (a) grafik kuat arus dan tegangan pada resistor terhadap waktu, (b) diagram fasor berdasarkan grafik (a)
(sumber : fundamentals of physics)
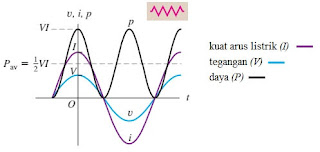
Gambar 9.
Grafik hubungan tegangan, kuat arus, dan daya terhadap waktu pada rangkaian
resistor murni.
(sumber:
physics university)
Rangkaian induktor pada arus bolak balik (AC)
Rangkaian induktor (L) murni disebut juga
sebagai rangkaian induktif yang terdiri dari sumber arus bolak-balik dan
sebuah induktor seperti gambar berikut.
Gambar 10.
Rangkaian induktor murni
(sumber:
physics university)
Pada rangkaian induktor
murni arus bolak balik yang mengalir pada induktor akan menyebabkan timbulnya
GGL induksi diantara ujung-ujung induktor tersebut. Jika pada sebuah induktor
dengan induktansi L arus yang mengalir dinyatakan dalam persamaan
IL = Im
sin ωt
Maka besar GGL induksi pada induktor (VL)
tersebut dapat dinyatakan dengan persamaan
Berdasarkan persamaan arus bolak balik dan tegangan
bolak balik di atas, maka kita dapat mengetahui bahwa pada rangkaian induktor
murni fase tegangan mendahului fase arus sebesar Φ = 900. Grafik hubungan tegangan dan arus bolak-balik
serta diagram fasor untuk rangkaian induktor murni adalah sebagai berikut.
Gambar 11.
(a) grafik hubungan tegangan dan arus bolak balik pada rangkaian induktif, (b)
diagram fasor
(sumber:
fundamentals of physics)
Untuk
diingat:
Persamaan tegangan dan
arus bolak balik pada induktor dapat pula ditulis sebagai berikut
I = Im sin (ωt
– 900)
V = Vm sin
ωt
Dikatakan bahwa fase
arus tertinggal dengan fase tegangan sebesar Φ = 900. Makna fisisnya tetap sama, sehingga pada penggambaran diagram fasor,
diagram fasor tegangan memiliki sudut yang lebih besar daripada diagram fasor
arus (ingat bahwa diagram fasor digambarkan berlawanan arah dengan jarum jam)
Reaktansi induktif
Nilai XL disebut sebagai reaktansi induktif yaitu sesuatu yang menghambat pada rangkaian induktor mirip dengan nilai hambatan pada rangkaian resistor. Reaktansi induktif juga memiliki satuan Ohm (Ω). Jika sumber arus mengalir dengan frekuensi (f) maka ω = 2πf sehingga besarnya reaktansi induktif dapat ditulis
Sifat induktor pada arus DC (frekuensi mendekati nol)
Perhatikan kembali
persamaan pada reaktansi induktor di atas, diketahui bahwa reaktansi induktif
berbanding lurus dengan frekuensi, sehingga ketika frekuensinya besar maka
reaktansinya juga akan semakin besar, begitu pula sebaliknya untuk frekuensi
yang mendekati nol (arus DC) maka reaktansi induktor juga mendekati nol.
Berdasarkan hal tersebut maka pada arus DC induktor tidak menghambat arus
DC.
Daya rangkaian induktor
Pada rangkaian induktor
tegangan mendahului kuat arus sebesar 900 hal ini berdampak pada
daya disipasi pada rangkaian induktor ini, pada suatu saat tertentu tegangan
dan arus akan bernilai positif sehingga daya juga bernilai positif (P = V .
I) yang artinya sumber arus bolak balik (AC) memberikan energi ke induktor
sedangkan pada saat yang lain tegangan dan arus akan bernilai negatif sehingga
daya juga bernilai negatif (P = V . I) yang artinya induktor mengirimkan
energi ke sumber arus bolak balik. Berdasarkan hal tersebut maka secara
bergantian daya pada induktor akan bernilai positif dan negatif, sehingga daya
rata-rata (Pav) pada induktor sama dengan nol.
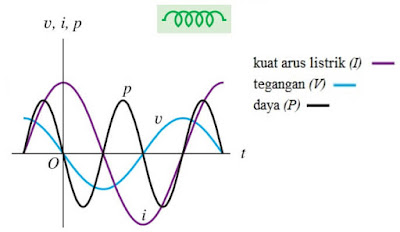
Grafik hubungan antara tegangan, kuat arus, dan
daya listrik terhadap waktu pada rangkaian induktor murni dapat dilihat pada
gambar di bawah ini.Gambar 12. Grafik hubungan tegangan, kuat arus, dan daya terhadap waktu pada rangkaian induktor murni.
(sumber:
physics university)
Rangkaian kapasitor pada arus bolak balik (AC)
Rangkaian kapasitor (C) murni disebut juga sebagai rangkaian kapasitif yang terdiri dari sumber arus bolak-balik dan sebuah kapasitor seperti gambar berikut.
Gambar 13.
Rangkaian kapasitor murni
(sumber:
physics university)
Kapasitor merupakan
salah satu komponen elektronika yang tersusun atas dua plat dengan ada medium
diantara keduanya yang terisolasi. Perlu diketahui bahwa, ketika kapasitor
dihubungkan dengan arus bolak balik aliran arus “tidak sama” dengan aliran arus
pada induktor atau resistor karena adanya medium diantara kedua plat yang
menyebabkan muatan tidak langsung mengalir. Akan tetapi pada kapasitor terjadi
fenomena “pengisian muatan listriik (arus listrik)” pada salah satu plat dan
“pengosongan muatan listrik (arus listrik)” pada plat yang lainnya. Arus
pengisian dan pengosongan ini sama besar. Cara pandang inilah yang dianggap
seolah-olah arus mengalir melalui kapasitor tersebut.
Jika kapasitor dialiri
oleh sumber arus bolak balik dengan tegangannya sesuai persamaan
VC = Vm
sin ωt
Pada kapasitor berlaku hubungan q = CV dan i =
dq/dt, maka berlaku hubunganBerdasarkan persamaan arus bolak balik dan tegangan bolak balik, maka dapat kita ketahui untuk rangkaian kapasitor murni fase arus bolak balik mendahului fase tegangan dengan perbedaan fase sebesar Φ = 900. Grafik hubungan tegangan dan arus bolak-balik serta diagram fasor untuk rangkaian kapasitor murni adalah sebagai berikut.
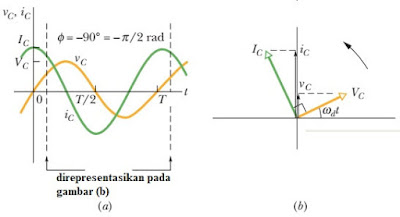
Gambar 14.
(a) grafik hubungan tegangan dan arus bolak balik pada rangkaian kapasitif, (b)
diagram fasor
(sumber:
fundamentals of physics)
Untuk diingat:
Persamaan tegangan dan
arus bolak balik pada kapasitor dapat pula ditulis sebagai berikut
V = Vm sin (ωt
– 900)
I = Im sin
ωt
Dikatakan bahwa fase
tegangan tertinggal dengan fase arus sebesar Φ = 900. Makna fisisnya tetap sama, sehingga pada penggambaran diagram fasor,
diagram fasor arus memiliki sudut yang lebih besar daripada diagram fasor
tegangan (ingat bahwa diagram fasor digambarkan berlawanan arah dengan jarum
jam)
Reaktansi
kapasitif
Telah dijelaskan
sebelumnya bahwa pada rangkaian kapasitor berlaku persamaan
iC = ωCVm
sin (ωt + 900)
Sesuai dengan hukum Ohm (V=IR), nilai
maksimal persamaan di atas dapat diubah menjadi
Nilai XC disebut sebagai reaktansi kapasitif
yaitu sesuatu yang menghambat pada rangkaian kapasitor mirip dengan nilai
hambatan pada rangkaian resistor. Reaktansi kapasitif juga memiliki satuan Ohm (Ω). Jika sumber arus mengalir dengan frekuensi (f)
maka ω = 2πf sehingga besarnya reaktansi kapasitif dapat ditulis
Sifat kapasitor pada arus DC (frekuensi mendekati nol)
Berdasarkan nilai
reaktansi kapasitif dapat kita ketahui bahwa ketika frekuensi berbanding
terbalik dengan reaktansi kapasitif, sehingga semakin besar frekuensi maka
reaktansi kapasitifnya semakin kecil. Akan tetapi ketika frekuensinya mendekati
nol (arus DC) maka reaktansinya akan sangat besar dan semakin menghambat kuat
arusnya, oleh karena itu arus searah tidak dapat mengalir melalui
kapasitor.
Daya rangkaian kapasitor
Mirip dengan rangkaian induktor, sebuah
kapasitor secara bergantian akan menyerap dan melepaskan energi dalam waktu
yang sama. Jadi, daya rata-rata pada rangkaian kapasitor adalah nol dan sebuah
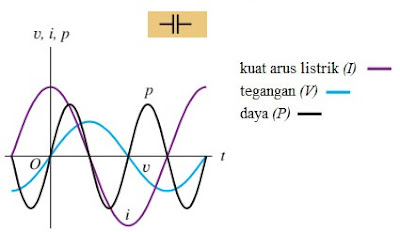
kapasitor pada rangkaian AC sama sekali tidak menggunakan energi. Grafik
hubungan antara tegangan, kuat arus, dan daya kapasitor pada rangkaian AC dapat
dilihat berikut ini
Gambar 15.
Grafik hubungan tegangan, kuat arus, dan daya terhadap waktu pada rangkaian
kapasitor murni.
(sumber:
physics university)
baca juga :
materi kelas 10 : kinematika gerak lurus bagian 1 dan bagian 2
materi kelas 11: fluida statis
materi kelas 10 : kinematika gerak lurus bagian 1 dan bagian 2
materi kelas 11: fluida statis
Rangkaian seri RLC pada arus bolak balik (AC)
Rangkaian seri RLC merupakan gabungan antara resistor (R), induktor (L), dan kapasitor (C) yang dirangkai secara seri seperti gambar berikut
16.
rangkaian seri resistor (R), induktor (L), dan kapasitor (C)
(sumber:
physics university)
Rangkaian seri RLC
seperti gambar di atas, dihubungkan dengan sumber arus bolak balik dengan besar
arus sebesar i=I sin ωt. Analisis rangkaian seri RLC dilakukan dengan
memperhatikan beberapa hal yakni
Pada rangkaian seri
kuat arus yang mengalir sama
Suatu sumber arus
listrik yang mengalir pada rangkaian adalah i=Im sin ωt, maka
semua komponen dalam rangkaian RLC akan memiliki kuat arus yang sama besar
Tegangan pada masing-masing
komponen memiliki karakteristik masing-masing.
Resistor : tegangan sefase dengan arus listrik bolak-balik
Vab = VR = Vm sin ωt
Induktor : fase tegangan mendahului dari fase arus listrik sebesar 900
Vbc = VL = Vm sin (ωt + 900)
Kapasitor : fase tegangan tertinggal dari fase arus listrik sebesar 900
Vcd = VC = Vm sin (ωt - 900)
Jika kita tetapkan sudut ωt sebagai acuan
sumbu x maka diagram fasor untuk kuat arus i, tegangan VR,
VL, dan VC dapat digambarkan sebagai berikut:
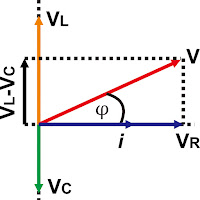
Gambar 17.
Diagram fasor pada rangkaian RLC
Berdasarkan diagram
fasor di atas, terlihat dengan jelas bahwa arus listrik (sumbu +x)
sefase dengan tegangan resistor (VR ke arah sumbu +x) ,
mendahului fase tegangan kapasitor (VC ke arah sumbu -y), dan
tertinggal dari fase tegangan induktor (VL ke arah sumbu +y).
Tegangan diantara ujung-ujung rangkaian RLC (Vad
= V) dapat ditentukan dengan penjumlahan secara vektor VR,
VL, dan VC sehingga didapatkan bahwa
Sudut yang terbentuk antara tegangan total (V)
dengan kuat arus disebut dengan beda sudut fase atau arah fasor V (φ) rangkaian seri RLC. Secara matematis dapat
dituliskan
Berdasarkan hukum Ohm (V=IR) maka persamaan di atas dapat pula ditulis
Persamaan di atas memberikan tiga konsekuensi logis pada nilai fase rangkaian RLC yakni
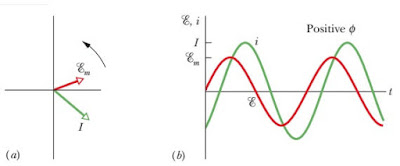
XL > XC : rangkaian RLC ini disebut dengan rangkaian
bersifat induktif (lebih induktif daripada kapasitif). Berdasarkan hal
tersebut maka tan φ akan bernilai positif yang berarti diagram fasor arus listrik (i)
berada di belakang (tertinggal dari) tegangan (V atau ε), pada grafik hubungan arus listrik dan tegangan
terhadap waktu ditandai dengan tegangan mencapai nilai maksimum lebih dahulu
daripada arus listrik mencapai nilai maksimumnya seperti terlihat seperti
gambar berikut ini.
Gambar 18.
(a) diagram fasor dan (b) grafik hubungan antara tegangan dan kuat arus listrik
terhadap waktu ketika tan φ bernilai positif
(sumber:
fundamentals of physics)
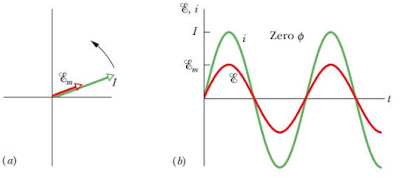
XL < XC : rangkaian RLC ini disebut dengan rangkaian
bersifat kapasitif (lebih kapasitif daripada induktif). Berdasarkan hal
tersebut maka tan φ akan bernilai negatif yang berarti diagram fasor arus listrik (i)
berada di depan (mendahului) tegangan (V atau ε), pada grafik hubungan arus listrik dan tegangan
terhadap waktu ditandai dengan tegangan mencapai nilai maksimum lebih lambat
daripada arus listrik mencapai nilai maksimumnya seperti terlihat seperti
gambar berikut ini.
Gambar 19.
(a) diagram fasor dan (b) grafik hubungan antara tegangan dan kuat arus listrik
terhadap waktu ketika tan φ bernilai negatif.
(sumber:
fundamentals of physics)
XL = XC : pada saat ini terjadi maka rangkaian RLC ini disebut
dengan istilah resonansi (akan dibahas lebih lanjut). Berdasarkan hal
tersebut maka tan φ akan bernilai nol yang berarti diagram fasor arus listrik (i)
berotasi bersama tegangan (V atau ε), pada grafik hubungan arus listrik dan tegangan terhadap waktu
ditandai dengan tegangan mencapai nilai maksimum bersamaan dengan arus listrik
mencapai nilai maksimumnya seperti terlihat seperti gambar berikut ini.
Gambar 20.
(a) diagram fasor dan (b) grafik hubungan antara tegangan dan kuat arus listrik
terhadap waktu ketika tan φ bernilai nol.
(sumber:
fundamentals of physics)
Impedansi (Z) rangkaian seri RLC pada arus bolak balik
Selain itu impedansi dapat juga ditentukan dari penerapan hukum Ohm secara langsung yakni
Daya rangkaian RLC pada arus bolak balik
Telah dijelaskan
sebelumnya bahwa baik induktor maupun kapasitor, sama-sama tidak ada daya
disipasinya (P = 0) karena ada perbedaan fase antara tegangan dan arus bolak
balik sebesar 900. Berbeda dengan kedua komponen tersebut, pada
resistor dimana tegangan dan arus listrik sefase sehingga daya rata-ratanya
selalu positif yang menandakan ada energi yang dikonsumsi oleh resistor ini.
Pada rangkaian
resistor, induktor, dan kapasitor besarnya daya ketika tegangan dan arus
memiliki beda fase sebesar Φ dapat ditulis dalam persamaan
P = vi = [V sin (ωt + Φ)][I sin ωt]
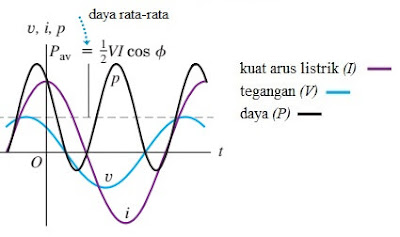
Grafik hubungan daya, tegangan, dan kuat arus dapat
dilihat pada grafik di bawah ini!
Gambar 21.
Grafik hubungan tegangan, kuat arus, dan daya terhadap waktu pada rangkaian RLC
(sumber:
physics university)
Berdasarkan grafik di
atas, luas daerah positif (di atas sumbu x) lebih besar daripada luas
daerah negatif (di bawah sumbu x). Hal ini berarti daya rata-rata dari
rangkaian RLC selalu bernilai positif. Kita dapat menurunkan persamaan daya
rata-rata dari persamaan di atas sehingga menjadi
P = [V(sin ωt cos Φ – cos ωt sin Φ)] [I sin ωt]
P = VI cos Φ sin2
ωt – VI sin Φ cos ωt sin ωt
Nilai rata-rata dari (cos
ωt) (sin ωt) sama dengan nol dan nilai (sin2 ωt) berubah-ubah secara
simetris dari 0 – 1 sehingga rata-ratanya adalah 1/2. Persamaan di atas dapat
kita tulis kembali sebagai.
Prata2 = ½ VI cos Φ
Prata2 = ½ √2 Irms √2 Vrms
cos ΦNilai cos Φ disebut dengan faktor daya untuk rangkaian resistor murni karena tegangan sefase dengan arus listrik maka Φ = 0, cos Φ = 1, dan Prata2 = Vrms Irms. pada rangkaian induktor murni maupun kapasitor murni nilai Φ = ±900, cos Φ = 0, dan Prata2 = 0. Sedangkan pada rangkaian RLC nilai faktor daya ini dapat ditentukan dengan menurunkan persamaan berikut ini
Prata2 = Vrms Irms
cos Φ
Karena pada rangkaian RLC daya disipasi hanya dihasilkan dari resistor,
maka berlaku Prata2=I2rms R, sehingga
I2rms R
= (Irms Z) Irms cos Φ
I2rms R = I2rms Z cos
ΦDalam rangkaian RLC faktor daya yang rendah tidak diinginkan, hal ini dikarenakan untuk memasok tegangan tertentu diperlukan kuat arus yang lebih besar sehingga menyebabkan kerugian pada saat transmisi. Untuk mengatasi hal tersebut, dapat dilakukan dengan cara menghubungkan kapasitor dengan beban secara paralel.
Resonansi rangkaian RLC pada arus bolak balik
Salah satu aplikasi
dari rangkaian seri RLC untuk merespon atau menerima sinyal dari sumber lain. Sebuah
pemancar radio yang mengirimkan suara melalui gelombang dengan frekuensi sudut
tertentu, sinyal radio ini akan diterima radio rumah (alat penerimanya adalah receiver
yang terbentuk dari rangkaian seri RLC). Setiap sinyal radio yang diberikan
oleh pemancar akan diterima oleh receiver dan menghasilkan arus dengan
frekuensi yang sama pada penerima. Akan tetapi hal ini masih belum cukup untuk
mendengarkan suara yang diberikan oleh pemancar karena arus terlalu kecil, untuk
itu receiver perlu diatur agar mendapatkan arus terbesar dan suara dari
pemancar dapat didengar oleh penerima. Arus terbesar ketika amplitudo arus terbesar
dan ini terjadi ketika frekuensi rangkaian RLC penerima sama dengan frekuensi
rangkaian RLC pemancar. Peristiwa ini yang disebut dengan resonansi rangkaian
seri RLC.
Resonansi ini dapat terjadi dengan mengatur
nilai impedansi dari rangkaian penerima sehingga frekuensi sudut rangkaian
penerima sama dengan frekuensi sudut rangkaian pemancar. Impedansi rangkaian
RLC dapat ditentukan sebagai berikut
Persamaan di atas menunjukkan
bahwa impedansi dipengaruhi oleh frekuensi sudut (ω) arus bolak balik, semakin
besar nilai ω, semakin besar XL, dan semakin kecil XC. Agar
lebih jelas perhatikan grafik logaritmik (agar dapat mencakup frekuensi sudut
yang besar) hubungan antara R, XL, XC, dan Z sebagai
fungsi ω berikut ini.
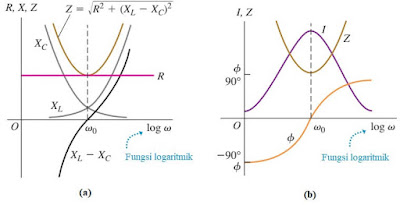
Gambar 22. (a) grafik hubungan R, XL, XC, dan Z sebagai fungsi ω, (b)
grafik I dan Z sebagai fungsi ω
(sumber: physics university)
Berdasarkan gambar 22.a terlihat ada satu titik (ketika frekuensinya sama
dengan ω0) dimana nilai XL sama dengan nilai XC sehingga
XL – XC sama dengan nol dan pada saat itu terjadi nilai
impedansi adalah minimum atau sama dengan nilai resistornya (Z = R). Impedansi
yang bernilai minimum ini menyebabkan kuat arus akan bernilai maksimum (I =
V/Z) sesuai dengan gambar 22.b. nilai frekuensi sudut ketika XL sama dengan XC
disebut frekuensi sudut resonansi. Secara matematis dapat ditulis
Karena ω = 2πf, maka persamaan di atas dapat ditulis
Demikian penjelasan singkat tentang rangkaian seri resistor, induktor,
dan kapasitor (RLC) pada arus bolak balik. Semoga bermanfaat bagi para pembaca
dan jika ada yang belum jelas bisa tinggalkan dikomentar.
untuk memantapkan penguasaan materi tentang rangkaian seri RLC pada arus bolak balik ini, silahkan mempelajari latihan soal tentang rangkaian seri RLC pada arus bolak balik ini
baca juga :
Soal UN fisika tahun 2019 lengkap dengan penjelasannya
Soal UN fisika tahun 2018 lengkap dengan penjelasannya
Soal UN fisika tahun 2017 lengkap dengan penjelasannya
Soal SBMPTN tahun 2018 kode 460 lengkap dengan penjelasannya
Soal UN fisika tahun 2018 lengkap dengan penjelasannya
Soal UN fisika tahun 2017 lengkap dengan penjelasannya
Soal SBMPTN tahun 2018 kode 460 lengkap dengan penjelasannya
Sumber :
Resnick,
R., Halliday, D., Walker, J. Fundamentals of Physics, 10th ed.,
John Wiley & Sons, Inc. 2014
Wolfson,
R. Essential university physics 2nd ed. Pearson education,
Inc.2012
Young, H. D., Freedman, R. A. Sears ana
Zemansky’s university physics : with modern physics 13th ed.,
Pearson education, Inc.2012








































Tidak ada komentar:
Posting Komentar