Ujian Nasional(UN)merupakan salah satu ujian yang diadakan oleh pemerintah untuk memetakan persebaran kualitas pendidikan di Indonesia. Pada era modern saat ini ujian nasional telah berganti dari yang semula menggunakan kertas sekarang menggunakan komputer atau yang dikenal sebagai UNBK (Ujian Nasional Berbasis Komputer). berdasarkan hal tersebut, disini saya menyediakan try out online UN Fisika kelas 12 yang disertai pembahasan di bawahnya dengan tujuan untuk membantu siswa kelas 12 dalam mempersiapkan Ujian Nasionalnya
pembahasan soal nomor 1 sampai 5:
pembahasan soal nomor 1:
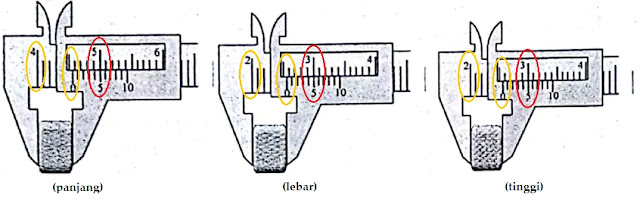
Perhatikan skala utama dan skala nonius yang ditunjukkan gambar
Warna kuning menunjukkan skala utama
Panjang : 4,5
Lebar : 2,5
Tinggi : 2,5
Warna merah menunjukkan skala nonius
Panjang : 5
Lebar : 5
Tinggi : 5
Jurus jitu :
Untuk menuliskan hasil
pengukuran jangka sorong seperti di atas, cukup tambahkan skala nonius di
belakang skala utama, sehingga hasil pengukurannya menjadi p = 4,55 cm, l =
2,55 cm, dan tinggi = 2,55 cm. semuanya terdiri dari 3 angka
penting, sehingga jawaban harus dalam 3 angka penting
Sehingga volume benda tersebut
adalah :
V = p x l x t
V = 4,55 x 2,55 x 2,55 = 29,58 = 29,6 cm3 (tiga
angka penting)
pembahasan soal nomor 2:
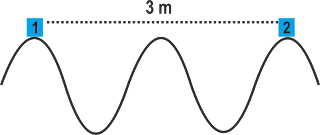
Ilustrasi soal:
Kecepatan benda ditentukan dengan persamaan
v = s / t
dimana s adalah perpindahan yang dialami benda.
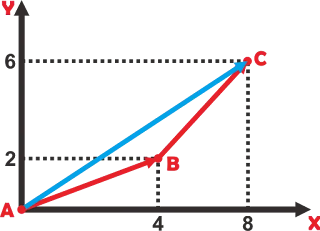
Perpindahan merupakan jarak terpendek yang diukur dari titik awal ke titik
akhir, berdasarkan gambar diatas kita dapat menggunakan persamaan phytagoras
sebagai berikut:
s2 = 82 + 62
s = 10 m (ingat angka cantik untuk phytagoras : 6,
8, 10)
sehingga kecepatan benda adalah
pembahasan soal nomor 3:
Tips : karena lantai licin dan katrol tidak berputar, maka
tegangan tali yang berhubungan dengan benda A dan B sama besar, sehingga sistem
dapat di analisis secara keseluruhan dengan benda B bergerak ke bawah (sebagai
gaya utama yang menggerakkan sistem) dan benda A bergerak ke kanan. Berdasarkan
hal tersebut maka hukum II Newton untuk soal ini adalah
pembahasan soal nomor 6 sampai 10:
pembahasan soal nomor 6:
Tips:
Perhatikan pada soal ditanyakan perbandingan energi
kinetik kedua benda saat sama-sama berada pada titik B. Berdasarkan hukum
kekekalan energi mekanik kita dapat mengetahui bahwa
EMA = EMB
EPA + EKA = EPB + EKB
(EKA = 0)
EPA -
EPB = EKB
ΔEP = EKB
mgΔh = EKB
perbandingan energi kinetik hanya bergantung
pada massa benda (massa sebanding dengan energi kinetik)
pembahasan soal nomor 7:
pembahasan soal nomor 8:
Roda D dan C bersinggungan ( vC = vD )
Roda C dihubungkan tali dengan roda A ( vC = vA )
Sehingga
vA = vD
ωA RA = ωD RD → Roda
A sepusat dengan roda B ( ωA = ωB )
Sehingga
ωB RA = ωD RD
50 . 30 = ωD 50
30 rad/s = ωD
pembahasan soal nomor 9:
pembahasan soal nomor 10:
Pernyataan 1
Benar, karena ciri dari tumbukan tak lenting adalah
setelah bertumbukan kedua benda bergerak bersama (koefisien restitusi sama
dengan nol)
Pernyataan 2
Benar, karena pada tumbukan tak lenting berlaku
hukum kekekalan momentum, tapi tidak berlaku hukum kekekalan energi kinetik
pembahasan soal nomor 11 sampai 15:
pembahasan soal nomor 11:
Hukum
bernoulli
P1
+ ½ ρv12 + ρgh1 = P2 + ½ ρv22
+ ρgh2
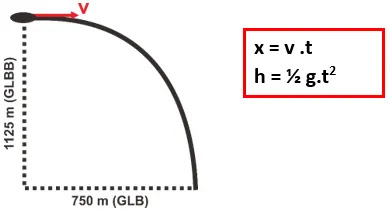
(P1
= P2 = P0, v1 << v2 sehingga
v1 = 0)
ρgh1
= ½ ρv22 + ρgh2
2g(h1
–h2) = v22
2 .
10 (1,2 – 0,4) = v22
20 .
0,8 = v22
16 =
v22
4 m/s = v2
pembahasan soal nomor 12:
Pada fenomena di atas, berlaku hukum kekekalan momentum
sudut dimana
LA = LB (perhatikan pilihan B dan
E)
Pada momentum Inersia
I = mR2
I sebanding dengan R2
RA > RB ,maka
IA > IB (pilhan E)
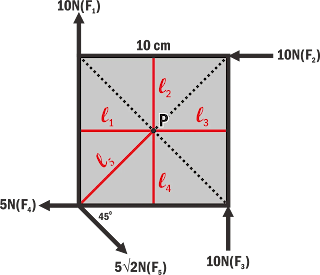
pembahasan soal nomor 13:
Untuk menentukan momen gaya, maka antara Gaya dan jarak harus saling
tegak lurus. Perhatikan gambar berikut:
Tanda negatif (-) menunjukkan bahwa benda
berputar berlawanan arah jarum jam
Dengan menggunakan persamaan τ
= F . R.
Tips :
Untuk mempermudah dalam
pengerjakan, dapat dibuat tabel momen gaya, gaya, dan jarak dengan ketentuan
untuk momen gaya yang searah jarum jam bernilai positif dan untuk
momen gaya berlawanan arah jarum jam bernilai negatif.
F (N)
|
ℓ (m)
|
(+ / - )
|
Τ (Nm)
|
10 N
|
0,05
|
+
|
+ 0,5
|
10 N
|
0,05
|
-
|
- 0,5
|
10 N
|
0,05
|
-
|
- 0,5
|
5 N
|
0,05
|
+
|
+ 0,25
|
5√2 N
|
0,05 √2
|
- 0,5
|
|
Total momen gaya
(Στ)
|
- 75
|
||
pembahasan soal nomor 14:
pembahasan soal nomor 15:
Benda bermassa memiliki gaya berat yang sebanding dengan
perubahan panjang sesuai dengan persamaan hukum Hooke
F = k Δx
pembahasan soal nomor 16 sampai 20:
pembahasan soal nomor 16:
Pilihan
3 benar, karena gelombang yang dapat dipolarisasikan hanya gelombang
transversal (cahaya termasuk gelombang transversal).
Pilihan 4 salah, karena cahaya dapat merambat
tanpa zat perantara seperti cahaya matahari yang melewati ruang angkasa untuk
sampai ke bumi.
pembahasan soal nomor 17:
Berdasarkan persamaan gelombang y = 40 sin (2πx) cos
(60πt) kita dapat mengetahui bahwa
k = 2π/λ
20 π = 2π/λ
λ = 0,1 m = 10 cm
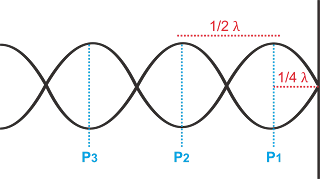
Selain itu nilai sin 20πx menunjukkan gelombang
ujung terikat seperti digambarkan berikut ini
Berdasarkan ilustrasi di atas, kita dapat mengetahui
bahwa
Letak perut pertama = 1/4 λ
Letak perut pertama = 1/4 . 10
Letak perut pertama = 2,5 cm
Perhatikan pilihan jawaban “B”
pembahasan soal nomor 18:
pembahasan soal nomor 21 sampai 25:
pembahasan soal nomor 21:
pembahasan soal nomor 22:
Mata tanpa akomodasi
Bayangan lensa objektif jatuh tepat di fokus lensa okuler
Bayangan lensa okuler jatuh di titik jauh mata (PR = ~)
Panjang teropong
d = s’ob + fok
21 = s’ob + 10
11 cm = s’ob
Mata berakomodasi maksimum
Bayangan lensa objektif jatuh di antara fokus lensa
okuler dan lensa okuler (ruang 1)
Bayangan lensa okuler jatuh di titik jauh mata (Sn = 30
cm)
S’ok = - 30 cm
maka
pembahasan soal nomor 23:
Persamaan matematis yang
digunakan
Q = m . c . ΔT
Kalor jenis berbanding terbalik
dengan perubahan suhu. Semakin besar kalor jenis benda, maka perubahan suhu
benda tersebut akan semakin kecil (benda semakin susah dipanasi). Sehingga
cAl > cTe >
cPe > cTi , maka
ΔTAl < ΔTTe < ΔTPe
< cTi
pembahasan soal nomor 24:
Untuk mengetahui kondisi akhir dari campuran, maka perlu
diketahui jumlah kalor yang dilepaskan oleh air untuk mencapai kesetimbangan
termal dan jumlah kalor yang diperlukan apabila seluruh es mencair.
·
Kalor yang
dilepaskan oleh air
Q1 = mair . cair. ΔTair
Q1 = 0,19048 . 4200 . 50
Q1 = 40000,8 J
·
Kalor yang
dibutuhkan es
Q2 = mes
. ces. ΔTes (mengubah suhu es dari -100C
menjadi 00C)
Q2 =
0,1 . 2100 . 10
Q2 =
2100 J
Q3 = mes
Les (mengubah wujud es
menjadi air)
Q3 =
0,1 . 336000
Q3 =
33600 J (untuk semua es yang mencair)
Sehingga kalor total yang diperlukan es adalah
Qes = Q2 + Q3
Qes = 2100 + 33600
Qes = 25700 J
Karena Q1 > Qes maka
semua es dapat mencair
pembahasan soal nomor 25:
Koefisien konduksi berbanding terbalik dengan perubahan
suhunya, sehingga kita hanya membandingkan antara keduanya saja. Bentuk
persamaan perbandingannya adalah
K1 . ΔT1 = K2 ΔT2
Sambungan logam PQ
KP . ΔTP = KQ ΔTQ
2KQ . (T2 – T1) = KQ
(T3 – T2)
2 (T2 – 20) = (T3 – T2)
2T2 – 40 = T3 – T2
3T2 – 40 = T3 ... (1)
Sambungan logam QR
KQ . ΔTQ = KR ΔTR
2KR . (T3 – T2) = KR
(T4 – T3)
2 (T3 – T2) = (90 – T3)
2T3 – 2T2 = 90 – T3
3T3 = 90 + 2T2
T3 = 30 + 2/3 T2 ... (2)
Substitusikan pers (1) ke pers (2)
3T2 – 40 = 30 + 2/3 T2
3T2 –
2/3 T2 = 70
7/3 T2 = 70
T2 = 30 0C
T3 = 50 0C
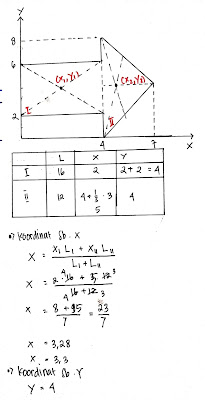
Jurus jitu:
Perbandingan koefisien konduksi logam P, Q, dan R adalah
KP = 2KQ = 4KR
KP : KQ : KR = 4 : 2 : 1
Karena koefisien konduksi berbanding terbalik dengan
perubahan suhu, maka perbandingan perubahan suhu pada logam P, Q, dan R adalah
ΔTP : ΔTQ : ΔTR = 1 : 2 : 4
Dari pilihan jawaban yang tersedia hanya pilihan jawaban
“D” yang paling sesuai
(30 – 20) : (50 – 30) : (90 – 50) = 1 : 2 : 4
10 : 20 : 40 = 1 : 2 : 4
pembahasan soal nomor 26 sampai 30:
pembahasan soal nomor 26:
Persamaan matematis yang digunakan
PV/T = konstan
Pernyataan (1) benar
Tekanan (P) sebanding dengan
suhu (T) pada volume tetap. Semakin besar tekanan, maka suhunya akan semakin
besar
Pernyataan (2) salah
Tekanan gas (P) bergantung dengan suhu (T) dan
atau volume gas (V)
pembahasan soal nomor 27:
pembahasan soal nomor 29:
1) sinar laser
termasuk kelompok gelombang elektromagnetik dalam kelompok cahaya tampak
2) sinar
inframerah, mempunyai frekuensi dan tingkat energinya lebih rendah
3) sinar X
mempunyai energi lebih kecil daripada sinar gamma
4) cahaya
tampak bermanfaat untuk penggunaan sinar laser dalam serat optik pada bidang
telekomunikasi dan kedokteran
5) sinar gamma dapat menembus pelat besi tipis
karena energinya sangat besar
pembahasan soal nomor 30:
AXZ
Menentukan nilai A
9 + A = 12 + 1
A = 4
Menentukan nilai Z
4 + Z = 6 + 0
Z = 2
Sehingga
4X2 → partikel alpha (α)
pembahasan soal nomor 31 sampai 35:
pembahasan soal nomor 31:
pembahasan soal nomor 32:
pembahasan soal nomor 34:
Hambatan 200 Ω dan 600 Ω dirangkai paralel, kemudian diseri dengan hambatan 400 Ω.
Maka hambatan total rangkaian adalah
Hambatan paralel
Rp = (R2 . R6)/ (R2 + R6)
Rp = (200 . 600)/ (200 + 600)
Rp = 120000/ 800
Rp = 150 Ω
Hambatan total
Rtot = R4 + RP + r
Rtot = 400 + 150 + 50
Rtot = 600 Ω
Pada rangkaian paralel
V2 = V6
I2 R2 = I6 R6
I2 . 200 = 2 . 600
I2 = 6 mA
Sehingga arus total rangkaian adalah
Itot = I2 + I6
Itot = 2 + 6
Itot = 8 mA
Maka ggl rangkaian tersebut adalah
ε = Itot Rtot
ε = 0,008 . 600
ε = 4,8 volt
pembahasan soal nomor 35:
Perhatikan kedua baterai
dirangkai seri dengan kutub positif baterai A terhubung dengan kutub negatif
baterai B, sehingga tegangan kedua baterai akan saling menguatkan (Vtot
= VA + VB).
Persamaan matematis yang digunakan adalah hukum
Ohm (V = IR). kuat arus berbanding terbalik dengan hambatan (baterai
tetap), sehingga berlaku persamaan perbandingannya
Jurus jitu:
Berdasarkan konsep “hambatan
berbanding terbalik dengan kuat arus listrik” maka semakin besar kuat arus
listrik, maka kuat arus yang mengalir akan semakin kecil.
Pada soal diketahui bahwa hambatan 2Ω diganti
dengan hambatan 12Ω (semakin besar) dan rangkaian merupakan rangkaian seri. Hal
ini akan mengakibatkan kuat arusnya
semakin kecil. Sehingga kuat arus setelah diganti hambatannya akan lebih kecil
daripada kuat arus sebelum diganti hambatannya (hanya pilihan C yang sesuai
dengan logika tersebut)
pembahasan soal nomor 36 sampai 40:
pembahasan soal nomor 36:
Persamaan umum untuk
ggl induksi adalah
ε = NBAω
sin ωt → persamaan sinusoidal ε = εmax
sin ωt
Periode
ω = 2π/T
ωT = 2π, sehingga berlaku
ω1 T1 = ω2
T2
ω 2 = ½ ω T2
4 = T2 (perhatikan
pilihan C dan E)
GGL maksimum
εmax = NBAω
εmax sebanding dengan jumlah lilitan
(N) dan kecepatan sudut (ω), sehingga
pembahasan soal nomor 37:
pembahasan soal nomor 38:
(2) dan (3) benar karena radio isotop Co-60 menghasilkan radiasi sinar
gamma yang digunakan untuk membunuh sel kanker dan mensterilkan alat kesehatan
pembahasan soal nomor 40:
Berdasarkan
hukum pergeseran wien
λmax
. T = C
panjang gelombang maksimum berbanding terbalik
dengan suhu
baca juga :
materi fisika tingkat SMA
latihan soal fisika tingkat SMA
soal UN Fisika SMA tahun 2018 dan pembahasannya
soal UN Fisika SMA tahun 2019 dan pembahasannya
materi fisika tingkat SMA
latihan soal fisika tingkat SMA
soal UN Fisika SMA tahun 2018 dan pembahasannya
soal UN Fisika SMA tahun 2019 dan pembahasannya









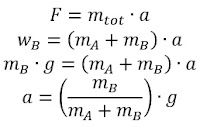




















Tidak ada komentar:
Posting Komentar