Analisis Dimensi
Misalkan kita akan menentukan dimensi dari gaya, maka dapat kita mulai dengan rumus untuk menentukan gaya yakni F = m . a, dimana percepatan a = v/t , kecepatan v = s . t. m, s, dan t merupakan besaran pokoknya, sehingga dimensi besaran gaya dapat ditentukan sebagai berikut
Tabel 6. Dimensi besaran-besaran turunan
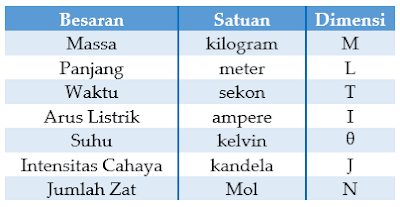
| Besaran | Simbol | Satuan | Dimensi |
| Kecepatan | v | ms-1 | [L][T]-1 |
| Percepatan | a | ms-2 | [L][T]-2 |
| Momentum Linier | p | kgms-1 | [M][L][T]-1 |
| Gaya | F | kgms-2 | [M][L][T]-2 |
| Usaha | W | kgm2s-2 | [M][L]2[T]-2 |
| Energi | E | kgm2s-2 | [M][L]2[T]-2 |
| Tekanan | P | kgm-1s-2 | [M][L]-1[T]-2 |
| Massa Jenis | ρ | kgm-3 | [M][L]-3 |
| Daya | P | kgm2s-3 | [M][L]2[T]-3 |
| Sudut | Θ | rad | 1 |
| Kecepatan Sudut | ω | rads-1 | [T]-1 |
| Percepatan Sudut | α | rads-2 | [T]-2 |
| Momentum Sudut | L | kgm2s-1 | [M][L]2[T]-1 |
| Momentum Inersia | I | kgm2 | [M][L]2 |
| Torsi | τ | kgm2s-2 | [M][L]2[T]-2 |
| Muatan Listrik | Q | C | [I][T] |
| Hambatan Listrik | R | Ω | [M][L]2[T]-3[I]-2 |
| Tegangan Listrik | V | volt | [M][L]2[T]-3[I]-1 |
| Kapasitas kapasitor | C | f | [M]-1[L]-2[T]4[I]2 |
| Fluks Magnet | Φ | Weber | [M][L]2[T]-2[I]-1 |
| Medan Magnet | B | T | [M][T]-2[I]-1 |
| Induktansi | L | H | [M][L]2[T]-2[I]-2 |
| Permeabilitas ruang vakum | μ0 | WbA-1m-1 | [M][L][T]-2[I]-2 |
| Permivitas ruang vakum | ε0 | C2N-1m-2 | [M]-1[L]-3[T]4[I]2 |
| Konstanta Gravitasi | G | m3kg-1s-2 | [L]3[M]-1[T]-2 |
| Konstanta Boltzman | K | JK-1 | [M][L]2[T]-2[θ]-1 |
| Bilangan Avogadro | NA | mol-1 | [N]-1 |
| Konstanta Planck | h | Js-1 | [M][L]2[T]-1 |
| Bilangan Gas Ideal | R | kgm2mol-1s-2T-1 | [M][L]2[T]-2[N]-1[θ]-1 |
| Kalor Jenis | c | Jkg-1K-1 | [L]2[T]-2[θ]-1 |
Dimensi satuan yang telah diuraikan di atas dapat memberikan beberapa manfaat antara lain.
- Analisis dimensi dapat digunakan untuk dua besaran fisika setara atau tidak
- Dapat digunakan untuk menentukan suatu persamaan yang pasti salah atau mungkin benar
- Dapat digunakan untuk menurunkan persamaan suatu besaran fisika jika kesebandingan besaran fisika tersebut terhadap besaran lainnya diketahui
Perhatikan dimensi dari besaran energi dan usaha pada tabel di atas, kedua besaran di atas memiliki dimensi yang sama [M][L]2[T]-2, sehingga dapat dikatakan kedua besaran tersebut setara.
Yang dimaksud dengan pasti salah adalah ketika dimensi antar besaran dalam suatu persamaan berbeda dan mungkin benar berarti jika persamaan tersebut dimensi antar besaran sudah sama dan tidak ada koesfisiennya, tapi jika dimensinya sudah sama tetapi persamaan aslinya ada koefisien, maka persamaan tersebut salah.
Dimensi pada dasarnya menunjukkan besaran penyusun dari suatu besaran turunan dan menunjukkan kesebandingannya, sehingga kita dapat menurunkan suatu rumus dari dimensinya, asalkan pada rumus tersebut tidak terdapat koefisien, misalnya pada rumus energi kinetik (EK = ½ mv2) ada koefisien ½ yang tidak dapat ditentukan dengan menggunakan analisis dimensi ini.
Penjumlahan dan pengurangan besaran dapat dilakukan jika besaran-besaran tersebut memiliki satuan yang sama, tapi jika satuannya berbeda tidak dapat dilakukan penjumlahan atau pengurangan. Untuk lebih jelasnya perhatikan contoh berikut
8 kg + 4 kg = 12 kg (bisa dijumlahkan)
8 kg – 4 kg = 4 kg (bisa dikurangkan)
8 kg + 4 N = ... (tidak bisa dijumlahkan karena satuannya berbeda)
Satuannya sama berarti dimensinya juga sama, sehingga dapat dikatakan suatu persamaan penjumlahan dan pengurangan dikatakan benar jika dimensi besarannya sama.
Contoh soal 1
Jarak s yang ditempuh oleh sebuah benda sebagai fungsi waktu t dinyatakan dalam persamaan s = At2 + Bt3 – Ct4. Tentukan dimensi untuk A, B, dan C !
Jika v = Pt + Qt2 + Rt3 dengan v dalam m/s dan t dalam s, tentukan satuan-satuan dari P, Q, dan R !








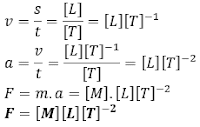
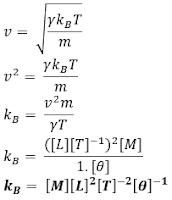




Tidak ada komentar:
Posting Komentar