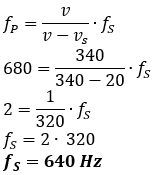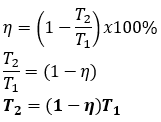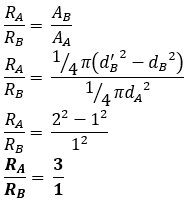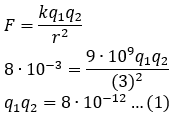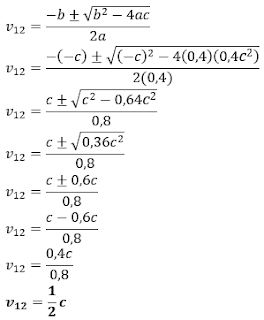LATIHAN SOAL UTBK 2022 - FISIKA | PAKET 1

Untuk mempersiapkan diri bagi siswa/i kelas 12 yang akan mengikuti UTBK tahun 2022, maka pada kesempatan kali ini saya akan memberikan beberapa latihan soal pada mata pelajaran Fisika. Soal – soal yang ada di bawah ini sudah disertai pembahasannya dan dihimpun dari berbagai sumber. Selamat menikmati

Soal nomor 1
Sebuah bola akan dilemparkan dari sebuah Balon udara yang memiliki ketinggian 20 m dari atas tanah. Bila pesawat bergerak dengan kecepatan konstan arah sumbu x positif sebesar 𝑣 saat menjatuhkan bola dengan percepatan gravitasi 10 𝑚/𝑠² ,Tentukan jarak antara bola dan balon udara setelah satu detik!
A. 10 m
B. 15 m
C. 20 m
D. 5 m
E. 0
Kunci jawaban: "B"

pembahasan soal nomor 1:

Berdasarkan soal dapat diketahui:
h = 20 m
g = 10 m/s²
t = 1 s
s ... ?
Karena pada awalnya bola dan balon bergerak bersama-sama dengan kecepatan v ke arah sumbu x positif, maka jarak antara bola dan balon merupakan jarak vertikalnya (sumbu y) yang mana bola melakukan gerak jatuh bebas. Sehingga untuk menyelesaikan soal ini kita dapat menggunakan persamaan
y = y₀ - v_oyt + ½ gt²
y = 20 - 0 + ½ 10 1²
y = 20 – 5
y = 15 m

Soal nomor 2
kawat timah dan kawat besi yang masing-masing memiliki panjang 35 cm dan 50 cm juga luas penampang 1 𝑐𝑚² 𝑑𝑎𝑛 1 𝑐𝑚² disambung dan kemudian digantung beban dengan massa 0,1 ton. Berapakah pertambahan panjang system gabungan kedua kawat tersebut?
(modulus young kawat timah = 3,5 𝑥 10¹⁰ 𝑁/𝑚² ,dan modulus young kawat besi = 2,5 𝑥 10¹⁰ 𝑁/ 𝑚²)
A. 0,1 mm
B. 0,2 mm
C. 0,3 mm
D. 0,4 mm
E. 0,5 mm
Kunci jawaban: "C"

pembahasan soal nomor 2:

Berdasarkan soal dapat diketahui
L₁= 35 cm = 35 x 10^-2 m
L₂ = 50 cm = 50 x 10^-2 m
A₁ = A₂ = 1 cm² = 10^-4 m²
m = 0,1 ton = 100 kg
E₁ = 3,5 𝑥 10¹⁰ 𝑁/𝑚²
E₂ = 2,5 𝑥 10¹⁰ 𝑁/𝑚²
Karena kedua kawat disambung hal itu berarti kedua kawat disambung secara seri. Sehingga konstanta pegas gabungan kedua kawat dapat ditentukan dengan persamaan

Ketika beban digantungkan maka pertambahan panjang kawat dapat ditentukan dengan persamaan
F = k . ∆x
m . g = k . ∆x
100 . 10 = 1/3 . 10⁷ . ∆x
10³ = 1/3 . 10⁷ . ∆x
∆x = 3 . 10^-4 m
∆x = 0,3 mm

Soal nomor 3
Sebuah kapal laut sedang berdiam di atas lautan. Seorang anak nakal dengan sengaja membuang koper milik ibunya ke dalam air. Apakah yang terjadi terhadap ketinggian laut? Asumsikan massa jenis koper lebih tinggi dari kapal beserta isinya!
A. Ketinggian laut naik karena ada benda yang dicelupkan ke dalam air
B. Ketinggian laut tetap karena koper awalnya juga berada di dalam kapal
C. Ketinggian laut turun sesaat saat koper dilempar oleh sang anak dan kembali ke posisi awal saat koper tenggelam seluruhnya
D. Ketinggian laut turun sesaat saat koper dilempar oleh sang anak dan kembali naik, namun lebih rendah dari posisi awal saat koper tenggelam seluruhnya
E. Ketinggian laut turun sesaat saat koper dilempar oleh sang anak dan kembali naik, namun lebih tinggi dari posisi awal saat koper tenggelam seluruhnya
Kunci jawaban: "D"

pembahasan soal nomor 3:

Pada mulanya kapal beserta isinya terapung di atas laut dengan sebagian kapal berada di dalam air laut. Hal ini sesuai dengan hukum Archimedes yang menyatakan bahwa besarnya gaya ke atas sama dengan besar zat cair yang dipindahkan, gaya ke atas inilah yang kemudian menahan kapal laut agar tetap terapung. Peristiwa terapungnya suatu benda dalam zat cair disebabkan karena massa jenis benda lebih kecil daripada massa jenis zat cair, semakin kecil massa jenis benda maka benda tersebut akan semakin terapung
Ketika sebuah koper dilemparkan, untuk beberapa saat berat kapal akan berkurang sehingga gaya ke atas juga akan semakin kecil akibatnya kapal sedikit terangkat dan permukaan air laut sedikit turun. namun ketika koper sudah jatuh ke laut, dengan berat yang sama (setelah koper dilempar) karena massa jenis koper lebih besar daripada massa jenis kapal maka volume koper yang dijatuhkan lebih kecil daripada volume kapal sehingga permukaan air laut akan naik sedikit tetapi lebih rendah dari posisi semula.

Soal nomor 4
Sebuah kalorimeter yang kapasitas kalornya 50 kal/⁰C berisi 200 gram air yang bersuhu 20⁰C. Kemudian ke dalam kalorimeter itu dimasukkan 100 gram es −10⁰C. Setelah dicapai kesetimbangan termis, massa es yang melebur adalah...
A. 43,75 gram
B. 56,25 gram
C. 62,50 gram
D. 68,25 gram
E. 80,00 gram
Kunci jawaban: "B"

pembahasan soal nomor 4:

Berdasarkan soal dapat diketahui
C_kal = 50 kal/⁰C
m_a = 200 g
T_a = 20⁰C
m_es = 100 g
T_es = -10⁰C
c_air = 1 kal/g⁰C
c_es = 0,5 kal/g⁰C
L_es = 80 kal/g
Massa es yang melebur?
Kita asumsikan bahwa suhu awal kalorimeter sama dengan suhu awal air yang berada di dalamnya. Ketika ke dalam kalorimeter tersebut dimasukkan sejumlah es maka terjadi perpindahan kalor dari air dan kalorimeter ke es, karena ditanyakan massa es yang melebur maka kita dapat mengetahui bahwa:

1. Tidak semua es mencair
2. Hanya sebagian es yang mencair, menunjukkan jumlah kalor yang dilepaskan oleh air dan kalorimeter tidak cukup untuk mencairkan seluruh es, meskipun suhunya mencapai 0 ⁰C
3. Batas akhir Suhu akhir air sistem adalah 0 ⁰C

Berdasarkan hal tersebut, maka jumlah kalor yang dilepaskan oleh air dan kalorimeter diserap oleh. Pada kondisi ini berlaku asas black yakni
Q_lepas = Q_serap
m_air . c_air . ∆T_air + C_kal . ∆T_kal = m_es . c_es . ∆T_es + m_es . L_es
200 . 1 . (20 – 0) + 50 . (20 – 0) = 100 . 0,5 . (0 – (-10)) + m_es . 80
4000 + 1000 = 500 + m_es . 80
4500 = m_es . 80
m_es = 56,25 gram

Soal nomor 5
Sebuah bola tenis bermassa 100 gram dilemparkan tegak lurus ke tembok dengan kecepatan 5 m/s. Bola tersebut menumbuk dinding selama 0,25 detik. Jika kecepatan bola setelah dipantulkan adalah 15 m/s, berapakah besar gaya yang diberikan tembok terhadap bola tersebut?
A. 2 N
B. 4 N
C. 5 N
D. 7,5 N
E. 8 N
Kunci jawaban: "E"

pembahasan soal nomor 5:

Berdasarkan soal dapat diketahui
m = 100 gram = 0,1 kg
v₁ = 5 m/s
∆t = 0,25 s
v₂ = -15 m/s (berlawanan arah karena memantul)
F .... ?
Soal tersebut tentang hubungan antara impuls dan momentum, sesuai dengan persamaan berikut
I = ∆p
F . ∆t = m . ∆v
F . ∆t = m (v₂ – v₁)
F . 0,25 = 0,1 ((-15) – 5)
F . 0,25 = -2
F = - 8 N
Tanda negatif menunjukkan arah gaya searah dengan kecepatan akhir benda setelah menumbuk tembok

Soal nomor 6
Kereta api bergerak dengan laju 72 km/jam menuju stasiun sambil membunyikan peluitnya. Bunyi peluit kereta api tersebut terdengar oleh kepala stasiun dengan frekuensi 680 Hz. Jika kelajuan bunyi di udara 340 m/s, maka frekuensi peluit kereta api tersebut adalah ....
A. 640 Hz
B. 680 Hz
C. 700 Hz
D. 720 Hz
E. 760 Hz
Kunci jawaban: "A"

pembahasan soal nomor 6:

Berdasarkan soal dapat diketahui
v_S = 72 km/jam = 20 m/s (mendekati)
f_P = 680 Hz
v = 340 m/s
f_S ... ?
persamaan untuk efek doppler pada soal di atas dapat ditulis

Jurus jitu :
Perhatikan bahwa kereta api bergerak mendekati stasiun, sehingga bunyi yang dikeluarkan kereta api akan terdengar lebih keras oleh orang yang berada di stasiun. Hal ini menunjukkan frekuensi bunyi yang di dengar oleh orang di stasiun (frekuensi pendengar atau f_P) lebih besar daripada frekuensi yang dikeluarkan oleh kereta api (frekuensi sumber atau f_S).
Jika kepala stasiun mendengar bunyi peluit dari kereta api dengan frekuensi 680 Hz, maka tentunya frekuensi peluit yang di keluarkan oleh kereta api kurang dari 680 Hz dan berdasarkan pilihan jawaban, kemungkinannya hanya pilihan A

Soal nomor 7
Suatu mesin Carnot mempunyai efisiensi 30% dengan temperature reservoir suhu tinggi sebesar 750 K. Agar efisiensi mesin naik menjadi 50% maka temperature reservoir suhu tinggi harus dinaikkan menjadi…
A. 1.050 K
B. 1.000 K
C. 950 K
D. 900 K
E. 850 K
Kunci jawaban: "A"

pembahasan soal nomor 7:

Berdasarkan soal dapat diketahui
η_A = 30%
T_1A = 750 K
η_B = 50%
T_1B = ...?
Hubungan antara efisiensi mesin Carnot dengan suhu reservoir dituliskan dalam persamaan berikut

Karna reservoir temperatur rendah tidak berubah untuk kedua keadaan maka, kita dapat menuliskan persamaan di atas menjadi
(1 – η_A)T_1A = (1 – η_B)T_1B
Persamaan di atas dapat dihafalkan sebagai rumus cepat menentukan reservoir suhu tinggi ketika efisiensinya berubah atau sebaliknya
(1 – 30%) 750 = (1 – 50%)T_1B
(1 – 0,3) 750 = (1 – 0,5) T_1B
0,7 . 750 = 0,5 T_1B
T_1B = 1050 K

Soal nomor 8
Dua buah konduktor (A dan B) terbuat dari bahan yang sama dengan panjang keduanya juga sama. Konduktor A merupakan kawat padat dengan diameter tampang lintang sebesar 1 m. Konduktor B merupakan kawat dengan penampang lintang berlubang dengan diameter dalam 1 m dan diameter luar 2 m. Besar perbandingan nilai hambatan R_A/R_B adalah....
A. 4
B. 3
C. 2
D. √2
E. 1
Kunci jawaban: "B"

pembahasan soal nomor 8:

Berdasarkan soal dapat diketahui:
d_A = 1 m
d_B = 1 m (diameter dalam kawat B)
d_B’ = 2 m (diameter luar kawat B)
R_A / R_B ....?
Persamaan untuk menentukan hambatan kawat adalah

Perhatikan bahwa luas penampang berbanding terbalik dengan hambatan, sehingga kita dapat menuliskan persamaan perbandingannya sebagai berikut

Soal nomor 9
Sebuah generator disuplai dengan 2.000 kg/s air yang mengalir melalui turbinnya dengan kelajuan 10 m/s. Jika generator mengubah 80% energi kinetik air menjadi energi listrik, daya listrik yang dihasilkan turbin adalah…
A. 40 kW
B. 80 kW
C. 400 kW
D. 800 kW
E. 4.000 kW
Kunci jawaban: "B"

pembahasan soal nomor 9:

Berdasarkan soal dapat diketahui
m/t = 2.000 kg/s
v = 10 m/s
η = 80%
P .... ?
Konsep pada soal di atas adalah perubahan energi kinetik menjadi energi listrik dengan efisiensi sebesar 80%, kita dapat menuliskannya dalam persamaan
η Ek = W
η ½ mv² = Pt
η ½ (m/t) v² = P
80% ½ (2000) 10² = P
0,8 100000 = P
P = 80.000 Watt
P = 80 kW

Soal nomor 10
Sebuah balok dengan berat 100 Newton diam pada sebuah bidang datar. Kemudian dari waktu t = 0 s sampai t = 5 s balok didorong dengan gaya konstan 40 Newton sejajar bidang datar. Koefisien gesek kinetik dan statis antara balok dan bidang datar berturut-turut adalah 0,2 dan 0,3. Dalam selang waktu antara t = 5s sampai t = 10s balok…
A. Bergerak dengan kecepatan tidak tetap
B. Bergerak dengan kecepatan tetap
C. Bergerak dengan percepatan tidak tetap
D. Bergerak kemudian akhirnya diam
E. Bergerak kemudian berhenti sebelum detik ke 10
Kunci jawaban: "D"

pembahasan soal nomor 10:

Berdasarkan soal dapat diketahui
F = 40 N
w = 100 N
μ_k = 0,2
μ_s = 0,3
soal di atas dapat diilustrasikan sebagai berikut

Percepatan yang dialami benda selama bekerja gaya F
ΣF = m a
F – f_k = m a
F – μ_k w = (w/g) a
40 – 0,2 . 100 = (100/10) a
40 – 20 = 10 a
20 = 10 a
a = 2 m/s²
kecepatan benda setelah bergerak 5 s (sampai di titik B)
v_B = v_A + at
v_B = 0 + 2 . 5
v_B = 10 m/s
setelah dari titik B gaya F ditiadakan tetapi masih ada gaya gesek kinetik yang menyebabkan benda mengalami perlambatan hingga berhenti di titik C dengan perlambatan sebesar
ΣF = m a
-f_k = m a
-20 = 10 a
a = - 2 m/s²
waktu sampai berhenti kembali
v_C = v_B – at
0 = 10 – 2t
t = 5 s jadi dibutuhkan waktu 5 detik dari titik B untuk membuat benda kembali berhenti atau dapat dikatakan benda berhenti pada saat t = 10 s jika dihitung dari titik awal A

Soal nomor 11
Pada sebuah bangku bermassa 40 kg diletakkan beban bermassa M seperti pada gambar.

Nilai maksimum M agar sistem masih berada dalam kesetimbangan adalah....
A. 120 kg
B. 100 kg
C. 80 kg
D. 60 kg
E. 40 kg
Kunci jawaban: "A"

pembahasan soal nomor 11:

Berdasarkan soal di ketahui
m_B = 40 kg (massa bangku)
M ... ? (massa beban)
Gaya-gaya yang bekerja pada sistem dapat diilustrasikan sebagai berikut

Karna diinginkan nilai maksimum dari M, maka gaya normal di titik P harus sama dengan nol (N_P = 0) atau bangku tidak terangkat di titik P, sehingga kita dapat mencari resultan torsinya dengan poros di titik Q,
Στ = 0 (poros di Q)
τ_B = τ_b
w_B . R_B = w_b . R_b
m_B . g . R_B = m_b . g . R_b
m_B . R_B = m_b . R_b
40 . 60 = M . 20
M = 120 kg

Soal nomor 12
Jika m₀ massa diam electron dan c laju cahaya di ruang hampa maka electron yang bergerak dengan kecepatan 0,8c memiliki energi kinetik sebesar…
A. 2 m₀c²
B. 5/3 m₀c²
C. 4/3 m₀c²
D. m₀c²
E. 2/3 m₀c²
Kunci jawaban: "E"

pembahasan soal nomor 12:

Berdasarkan soal dapat diketahui
v = 0,8 c
Ek = .... ?
Karna
v = 0,8 c
v = 8/10 c
maka dengan menggunakan hubungan phytagoras, (baca : jurus jitu menyelesaikan soal relativitas khusus)
γ = 10/6
γ = 5/3
jadi energi kinetiknya dapat ditentukan dengan cara>
Ek = (γ – 1) E0
Ek = (5/3 – 1)m₀c²
Ek = 2/3 m₀c²

Soal nomor 13
Permukaan sebuah lempeng logam natrium disinari dengan seberkas foton berenergi 4,43 eV. Jika fungsi kerja natrium adalah 2,28 eV maka energy kinetic maksimum electron yang dihasilkan adalah…
A. 2,15 eV
B. 2,28 eV
C. 4,56 eV
D. 6,71 eV
E. 8,86 eV
Kunci jawaban: "A"

pembahasan soal nomor 13:

Berdasarkan soal dapat diketahui
E = 4,43 eV
W₀ = 2,28 eV
EK_maks ...?
Pada efek fotolistrik berlaku persamaan
EK_maks = E – W₀
EK_maks = 4,43 – 2,28
EK_maks = 2,15 eV

Soal nomor 14
Dua lampu pijar identik dengan spesifikasi 100 watt, 110 volt, dihubungkan paralel pada tegangan 110 volt. Daya total kedua lampu adalah…
A. 100 W
B. 125 W
C. 150 W
D. 175 W
E. 200 W
Kunci jawaban: "E"

pembahasan soal nomor 14:

Karena kedua lampu di pasang paralel maka tegangan yang bekerja pada lampu sama dengan tegangan sumber yakni 110 volt. Sehingga berdasarkan spesifikasinya ketika diberi tegangan 110 volt daya lampu adalah 100 watt,. Jadi daya total kedua lampu sama dengan 100 + 100 = 200 watt

Soal nomor 15
Jumlah muatan dari dua buah muatan q₁ dan q₂ adalah -6µC. Jika kedua muatan tersebut dipisahkan sejauh 3 m maka masing-masing muatan akan merasakan gaya listrik sebesar 8mN. Besar q₁ dan q₂ berturut-turut adalah…
A. -5µC dan -1µC
B. -10µC dan -4 µC
C. -3 µC dan -3 µC
D. -8 µC dan 2 µC
E. -4 µC dan -2 µC
Kunci jawaban: "E"

pembahasan soal nomor 15:

Berdasarkan soal dapat diketahui
q₁ + q₂ = -6μC = -6 x 10^-6 C
r = 3 m
F = 8 mN = 8 x 10^-3 N
q₁ dan q₂ ...?
karena jumlah kedua muatan adalah negatif, maka muatan-muatan tersebut adalah elektron dan proton, berdasarkan hukum Coulomb kita dapat menuliskan

Berdasarkan soal maka
q₁ + q₂ = -6 ∙ 10^-6
q₁ = - q₂ -6 ∙ 10^-6 ...(2)

Substitusikan persamaan (2) ke persamaan (1)
(-q₂ – 6 . 10^-6) q₂ = 8 . 10^-12
-( q₂)² – 6 . 10^-6 q₂ = 8 . 10^-12
q₂2 + 6 . 10^-6 q₂ + 8 . 10^-12 = 0
(q₂ + 4 . 10^-6) (q₂ + 2 . 10^-6) = 0
q₂ = - 4 . 10^-6 atau q₂ = - 2 . 10^-6
jika q₂ = - 4 . 10^-6, maka q₁ = - 2 . 10^-6
jika q₂ = - 2 . 10^-6, maka q₁ = - 4 . 10^-6

Soal dan Pembahasan | Teori Relativitas Khusus Einsten (Fisika Kelas 12)

Soal dan pembahasan : relativitas khusus Einstein ditulis sebagai bahan belajar atau referensi untuk membuat soal-soal ulangan harian, yang mana materi relativitas khusus Einstein dipelajari oleh siswa pada kelas 12 semester genap. Sebagian besar siswa menganggap bahwa materi relativitas khusus Einstein sebagai salah satu materi fisika yang sulit dipahami, oleh karena itu dengan artikel ini semoga dapat menambah pemahaman kepada para pembaca dalam memahami materi relativitas khusus Einstein. Sebelum melanjutkan membaca soal dan pembahasan relativitas khusus Einstein, silahkan dibaca juga artikel kami yang berjudul Jurus Jitu : Menyelesaikan Soal Relativitas Khusus Einstein, disana para pembaca akan menemukan beberapa tips dan trik yang saya sebut jurus jitu sebagai hasil apa yang saya peroleh dalam mempelajari materi ini dan saya gunakan untuk membuat pembahasan dalam soal-soal di bawah ini. Selamat membaca.

Soal nomor 1

Sebuah partikel yang bergerak dengan kelajuan 0,3c terhadap kerangka acuan laboratorium memancarkan sebuah elektron searah dengan kecepatan 0,3c relatif terhadap partikel. Laju elektron tadi menurut kerangka acuan laboratorium paling dekat nilainya dengan ...
A. 0,32c
B. 0,51c
C. 0,66c
D. 0,76c
E. 0,90c
Kunci jawaban: "B"

pembahasan soal nomor 1:

Soal di atas dapat diilustrasikan sebagai berikut

v_PL = 0,3c (kecepatan partikel relatif terhadap lab)
v_EP = 0,3c (kecepatan elektron relatif terhadap partikel)
v_EL = ...? (kecepatan elektron relatif terhadap lab)
persamaan umum untuk penjumlahan relativistiknya dapat ditulis

Soal nomor 2

Dua roket saling mendekat dengan kelajuan sama relatif terhadap bumi. jika kelajuan relatif roket satu terhadap roket lainnya adalah 0,80c maka kelajuan roket adalah ....
A. 0,40c
B. 0,50c
C. 0,60c
D. 0,70c
E. 0,75c
Kunci jawaban: "B"

pembahasan soal nomor 2:

Soal di atas dapat diilustrasikan sebagai berikut :

v_1B = v (kecepatan pesawat 1 relatif terhadap bumi)
v_2B = -v (kecepatan pesawat 2 relatif terhadap bumi)
v₁₂ = 0,8c (kecepatan pesawat 1 relatif terhadap pesawat 2)
v ... ?
persamaan umum penjumlahan relativitasnya dapat ditulis

Untuk persamaan di atas kita dapat menggunakan rumus abc, dimana a = 0,4, b = (-c), dan c = 0,4c² seperti berikut ini

Soal nomor 3

Perbandingan dilasi waktu untuk sistem yang bergerak pada kecepatan 0,8c (c = cepat rambat cahaya) dengan sistem yang bergerak dengan kecepatan 0,6c adalah ....
A. 3 : 4
B. 4 : 3
C. 9 : 2
D. 9 : 16
E. 16 : 9
Kunci jawaban: "B"

pembahasan soal nomor 3:

Berdasarkan soal dapat diketahui
v₁ = 0,8c
v₂ = 0,6c
Δt₁ : Δt₂ = ... ?
Persamaan untuk dilatasi waktu adalah
Δt = γ Δt₀ ... (1)
Dengan menggunakan kecepatan dan konsep phytagoras (baca jurus jitu) kita dapat menentukan nilai γ sebagai berikut:
v₁ = 0,8c
v₁ = 8/10 c
sisi siku-siku = 8
sisi miring = 10
sisi siku-siku lainnya = 6
γ₁ = 10/6
v₂ = 0,6c
v₂ = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya = 8
γ₂ = 10/8
berdasarkan persamaan (1) kita dapat menuliskan persamaan perbandingannya

Soal nomor 4

Sebuah cincin berbentuk lingkaran diam dalam kerangka S seperti ditunjukkan dalam gambar.

Bentuk cincin menurut pengamat O’ adalah ....

Kunci jawaban: "C"

pembahasan soal nomor 4:

Karena pengamat O’ berada pada kerangka acuan S’ yang bergerak dalam arah sumbu x dengan kecepatan mendekati kecepatan cahaya, maka jari – jari lingkaran yang sejajar dengan sumbu x akan mengalami kontraksi panjang sehingga panjangnya menjadi lebih kecil dari panjang jari-jari semula. Oleh karena itu bentuknya akan menyempit dalam arah vertikal seperti pada gambar C

Soal nomor 5

Sebuah pesawat ruang angkasa yang panjangnya 6 m bergerak dengan kecepatan 2,7 x 10⁸ m/det. Panjang pesawat menurut pengamat yang diam di bumi adalah ....
A. 1,9 m
B. 2,6 m
C. 4,0 m
D. 8,0 m
E. 19 m
Kunci jawaban: "B"

pembahasan soal nomor 5:

L₀ = 6m
v = 2,7 x 10⁸ m/s
v = (2,7 x 10⁸)/3 x 10⁸
v = 0,9c
L ... ?
Menentukan nilai “γ”
v = 0,9c
v = 9/10 c
sisi siku-siku = 9
sisi miring = 10
sisi siku-siku lainnya
x² = 10² – 9²
x² = 100 – 81
x² = 19
x = √19
x = 4,4 m
jadi nilai γ
γ = 10/4,4

persamaan untuk relativitas panjang

Soal nomor 6

Sebuah kubus memiliki volume sejati 1000 cm³. Volum kubus tersebut menurut seseorang pengamat yang bergerak dengan kecepatan 0,8c relatif terhadap kubus dalam arah sejajar salah satu rusuknya adalah ....
A. 100 cm³
B. 300 cm³
C. 400 cm³
D. 500 cm³
E. 600 cm³
Kunci jawaban: "E"

pembahasan soal nomor 6:

Berdasarkan soal dapat diketahui
V₀ = 1000 cm³
v = 0,8c
V ... ?
Menentukan nilai “γ”
v = 0,8c
v = 8/10 c
sisi siku-siku = 8
sisi miring = 10
sisi siku-siku lainnya (x) = 6
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/6

karena kubus bergerak sejajar dengan salah satu rusuknya, maka hanya satu rusuk yang mengalami konstraksi panjang, sehingga hubungan antara volume diam dengan volume bergerak kubus dapat ditulis
V₀ = L₀³ (Volume diam kubus)
V = L³ (Volume bergerak kubus)
V = L . L²
V = L₀ / γ . L₀²
V = L₀³ / γ
V = V₀ / γ
V = 1000 / (10/6)
V = 1000 . 6 / 10
V = 600 cm³

Soal nomor 7

Sebuah benda mempunyai massa diam 2 kg. Bila benda bergerak dengan kecepatan 0,6c, maka massanya akan menjadi ....
A. 2,6 kg
B. 2,5 kg
C. 2,0 kg
D. 1,6 kg
E. 1,2 kg
Kunci jawaban: "B"

pembahasan soal nomor 7:

Berdasarkan soal dapat diketahui
m₀ = 2 kg
v = 0,6c
m ... ?
Menentukan nilai “γ”
v = 0,6c
v = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya (x) = 8
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/8

persamaan untuk massa relativistik adalah
m = γm₀
m = (10/8) 2
m = 2,5 kg

Soal nomor 8

Sebuah kubus dengan massa jenis 3200 kg/m³ bergerak dengan kelajuan 0,6c sejajar salah satu rusuknya terhadap pengamat O. Massa jenis kubus itu bila diukur oleh pengamat O adalah (dalam kg/m³) ....
A. 2560
B. 3200
C. 4000
D. 5000
E. 5400
Kunci jawaban: "D"

pembahasan soal nomor 8:

Berdasarkan soal dapat diketahui
ρ₀ = 3200 kg/m³
v = 0,6c
ρ .... ?
Menentukan nilai “γ”
v = 0,6c
v = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya (x) = 8
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/8

Hubungan antara massa jenis relativistik (ρ) dan massa jenis diamnya (ρ₀) dapat ditentukan dengan persamaan berikut ini

Soal nomor 9

Agar energi kinetik benda bernilai 20% energi diamnya dan c adalah kelajuan cahaya dalam ruang hampa, maka benda harus bergerak dengan kelajuan ....
A. c/4
B. c/2
C. c√11 /6
D. c√2 /3
E. c√13 /6
Kunci jawaban: "C"

pembahasan soal nomor 9:

Berdasarkan soal dapat diketahui
EK = 20 E₀
v ... ?
persamaan energi kinetik relativistik dapat ditulis
EK = (γ – 1)E₀
20%E0 = (γ – 1)E₀
0,2 = γ – 1
γ = 1,2
γ = 12/10, dimana
12 merupakan sisi miring
10 merupakan sisi siku-siku
Dengan menggunakan konsep phytagoras kita dapat menentukan sisi siku-siku lainnya yakni
x² = 12² – 10²
x² = 144 – 100
x² = 44
x = 2√11
sehingga kecepatan benda adalah

Soal nomor 10

Jika energi total proton adalah empat kali energi diamnya, maka kelajuan proton adalah ... (c = kecepatan cahaya)
A. 2/3 √2 c
B. 1/4 √15 c
C. 3/5 √3 c
D. 1/2 √11 c
E. 1/6 √5 c
Kunci jawaban: "B"

pembahasan soal nomor 10:

Berdasarkan soal dapat diketahui
E = 4E₀
v .... ?
persamaan energi total relativistik dapat ditulis
E = γE₀
4E₀ = γE₀
γ = 4
γ = 4/1, dimana
4 merupakan sisi miring
1 merupakan sisi siku-siku
Dengan menggunakan konsep phytagoras kita dapat menentukan sisi siku-siku lainnya
x² = 4² – 1²
x² = 16 – 1
x² = 15
x = √15
sehingga kecepatan benda tersebut adalah

Soal nomor 11

Sebuah pesawat bergerak dengan kecepatan 0,6c terhadap bumi. dari pesawat ditembakkan peluru dengan kecepatan 0,4c searah dengan pesawat. kecepatan peluru terhadap bumi adalah ....
A. c
B. 0,8c
C. 0,6c
D. 0,5c
E. 0,2c
Kunci jawaban: "B"

pembahasan soal nomor 11:

Soal di atas dapat diilustrasikan sebagai berikut

v_PB = 0,6c (kecepatan pesawat relatif terhadap bumi)
v_RP = 0,4c (kecepatan peluru relatif terhadap pesawat)
v_RB = ... ? (kecepatan peluru relatif terhadap bumi)
tuliskan persamaan umumnya sebagai berikut

Soal nomor 12

Pada sebuah dinding tegak terdapat gambar sebuah segitiga sama sisi dengan panjang sisi 3 . Seandainya gambar tersebut dilihat oleh orang yang sedang berada di dalam pesawat yang bergerak sejajar dengan dinding dengan kecepatan 0,60c, maka luas segitiga tersebut adalah ....

A. √3 ms²
B. 1,8√2 m²
C. 1,8√3 m²
D. 2,4√3 m²
E. 3√3 m²
Kunci jawaban: "C"

pembahasan soal nomor 12:

Menentukan nilai “γ”
v = 0,6c
v = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya (x) = 8
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/8

karena pesawat bergerak sejajar dengan dinding, maka bagian segitiga yang mengalami kontraksi panjang adalah tinggi segitiga tersebut. perhatikan ilustrasi berikut
gambar 12
tinggi diam segitiga sama sisi adalah
t₀² = 3² – 1,5²
t₀² = (2 . 1,5)² – 1,5²
t₀² = (22 – 1) 1,5²
t₀² = (4 – 1) . 1,5²
t₀² = 3 . 1,5²
t₀ = 1,5√3 m
hubungan antara luas diam dengan luas bergeraknya adalah
gambar 12a

Soal nomor 13

Ada dua anak kembar A dan B. A berkelana di antariksa dengan pesawat antariksa yang berkecepatan 0,8c. setelah 12 tahun berkelana A pulang ke bumi. menurut B perjalanan A telah berlangsung selama ...
A. 20 tahun
B. 15 tahun
C. 12 tahun
D. 10 tahun
E. 8 tahun
Kunci jawaban: "A"

pembahasan soal nomor 13:

Berdasarkan soal dapat diketahui
Δt₀ = 12 tahun
v = 0,8c
Δt ... ?
Menentukan nilai “γ”
v = 0,8c
v = 8/10 c
sisi siku-siku = 8
sisi miring = 10
sisi siku-siku lainnya (x) = 6
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/6
persamaan dilatasi waktu adalah
Δt = γΔt0
Δt = 10/6 Δt0
Δt = 10/6 . 12
Δt = 20 tahun

Soal nomor 14

Bila laju partikel 0,6 c, maka perbandingan massa relativistik partikel itu terhadap massa diamnya adalah ....
A. 5 : 3
B. 25 : 9
C. 5 : 4
D. 25 : 4
E. 8 : 5
Kunci jawaban: "C"

pembahasan soal nomor 14:

Berdasarkan soal dapat diketahui
v = 0,6c
m : m₀ = ...?
Menentukan nilai “γ”
v = 0,6c
v = 6/10 c
sisi siku-siku = 6
sisi miring = 10
sisi siku-siku lainnya (x) = 8
(pasangan triple phytagoras)
jadi nilai γ
γ = 10/8

persamaan untuk massa relativistik adalah
m = γ m₀
m : m₀ = γ
m : m₀ = 10 : 8
m : m₀ = 5 : 4

Soal nomor 15

Sebuah elektron bergerak dengan kecepatan v = 1/12 c √23 . pernyataan yang benar adalah ....
(1) Massa geraknya = 12/11 x massa diamnya
(2) Energi totalnya = 12/11 x energi diamnya
(3) Energi kinetiknya = 1/11 x energi diamnya
(4) Energi totalnya = 11/12 x energi diamnya
Kunci jawaban: “A” (1, 2, 3 benar)

pembahasan soal nomor 15:

Berdasarkan soal dapat diketahui
v = 1/12 c √23

menentukan nilai γ
v = √23/12 c , dimana
√23 merupakan sisi siku-siku
12 merupakan sisi miring
Dengan menggunakan konsep phytagoras kita dapat menentukan panjang sisi siku-siku satunya sebagai berikut
x² = 12² – (√23)²
x² = 144 – 23
x² = 121
x = 11
sehingga nilai γ adalah
γ = 12/11

persamaan massa relativistik
m = γ m₀
m = 12/11 m₀
pernyataan 1 benar

persamaan energi relativistik
EK = (γ – 1) E₀
EK = (12/11 – 1) E₀
EK = 1/11 E₀
Pernyataan 3 benar

EKtot = γE₀
EKtot = 12/11 E₀
Pernyataan 2 benar dan pernyataan 4 salah

Soal nomor 16

Sebuah pesawat mempunyai massa diam m₀ bergerak dengan kecepatan mendekati kecepatan cahaya sehingga massanya menjadi 1 ¼ x massa diamnya. Jika kecepatan cahaya c, maka energi kinetik benda itu adalah ....
A. 0,25 m₀c²
B. 0,5 m₀c²
C. m₀c²
D. 1,25 m₀c²
E. 1,5 m₀c²
Kunci jawaban: "A"

pembahasan soal nomor 16:

Berdasarkan soal dapat ditulis
m = 1 ¼ m₀
m = 5/4 m₀
EK ...?
Berdasarkan persamaan untuk massa relativistik
m = γ m₀
maka kita dapat mengetahui bahwa
γ = 5/4

persamaan energi relativistik adalah
EK = (γ – 1) E₀
EK = (5/4 – 1)m₀c²
EK = ¼ m₀c²
EK = 0,25 m₀c²

Soal nomor 17

Agar energi kinetik benda bernilai 25% energi diamnya dan c adalah kecepatan cahaya dalam ruang hampa, maka benda harus bergerak dengan kelajuan ....
A. c/4
B. c/2
C. 3c/5
D. 3c/4
E. 4c/5
Kunci jawaban: "C"

pembahasan soal nomor 17:

Berdasarkan soal dapat diketahui
EK = 25% E₀
EK = 0,25 E₀
v ... ?
persamaan untuk energi relativistik
EK = (γ – 1) E₀
0,25 E₀ = (γ – 1) E₀
0,25 = γ – 1
γ = 1,25
γ = 5/4, dimana
sisi siku-siku = 4
sisi miring = 5
sisi siku-siku lainnya (x) = 3
(pasangan triple phytagoras)
Jadi besar kecepatan v
v = 3/5 c

Soal nomor 18

Periode suatu pendulum di muka bumi besarnya 3,0 detik. Bila pendulum tersebut diamati oleh seseorang yang bergerak relative terhadap bumi dengan kecepatan 0,95c, maka periode pendulum tersebut dalam detik adalah ....
A. 0,5
B. 1,5
C. 9,6
D. 15
E. 300
Kunci jawaban: "D"

pembahasan soal nomor 18:

Δt₀ = 3,0 s
v = 0,95c
Δt ... ?
menentukan nilai γ
v = 0,95c
v = 95/100 c , dimana
95 merupakan sisi siku-siku
100 merupakan sisi miring
Dengan menggunakan konsep phytagoras kita dapat menentukan panjang sisi siku-siku satunya sebagai berikut
x² = 100² – 95²
x² = 10000 – 9025
x² = 975
x² = √975
x = 31,22

sehingga nilai γ adalah
γ = 100/31,22
γ = 3,2
Persamaan relativitas dilatasi waktu
Δt = γ Δt₀
Δt = 3,2 . 3,0
Δt = 9,6 s

Soal nomor 19

Sebuah pesawat bergerak dengan laju relativistic v. sebuah peluru bermassa diam m ditembakkan searah dengan pesawat dengan laju v relatif terhadap pesawat. jika v = 2/3 c dengan c adalah laju cahaya, maka menurut pengamat di bumi energi total peluru tersebut adalah ....
A. 10mc²/5
B. 11mc²/5
C. 12mc²/5
D. 13mc²/5
E. 15mc²/5
Kunci jawaban: "D"

pembahasan soal nomor 19:

Karna pengamat merupakan orang yang diam di bumi, maka energi kinetiknya juga berdasarkan orang yang diam di bumi, untuk itu kita perlu menentukan besar kecepatan peluru relatif terhadap bumi. Soal di atas dapat diilustrasikan sebagai berikut

v_PB = 2c/3 (kecepatan pesawat relatif terhadap bumi)
v_RP = 2c/3 (kecepatan peluru relatif terhadap pesawat)
v_RB = ... ? (kecepatan peluru relatif terhadap bumi)
tuliskan persamaan umumnya sebagai berikut

Menentukan nilai “γ”
v = 12/13 c
sisi siku-siku = 12
sisi miring = 13
sisi siku-siku lainnya (x) = 5
(pasangan triple phytagoras)
jadi nilai γ
γ = 13/5

menentukan energi total
Etot = γ E₀
Etot = 13mc²/5

Soal nomor 20

Sebuah partikel bermassa diam m0 bergerak sedemikian rupa sehingga energi totalnya adalah 2 kali energi diamnya. Partikel ini menumbuk partikel diam yang bermassa m0 dan keduanya membentuk partikel baru. Momentum partikel baru adalah ....
A. 3√2 m₀c
B. 3 m₀c
C. 2 m₀c
D. √3 /3 m₀c
E. √3 m₀c
Kunci jawaban: "E"

pembahasan soal nomor 20:

Berdasarkan soal dapat diketahui
Etot = 2 E₀
p ... ?
persamaan untuk relativitas energi dan momentum adalah
Etot² = E₀² + (pc)²
(2E₀)² = E₀² + (pc)²
4E₀² = E₀² + (pc)²
3E₀² = (pc)²
pc = √3 E₀
pc = √3 m₀c²
p = √3 m₀c

demikian beberapa soal dan pembahasan tentang materi Teori Relativitas Khusus Einstein, semoga bisa memberikan manfaat kepada para pembaca. jika ada yang ingin bertanya atau menyampaikan saran dan kritik bisa ditulis di kolom komentar

Jurus Jitu : Menyelesaikan Soal Relativitas Khusus Einstein

Materi relativitas khusus Einstein dipelajari oleh siswa kelas 12 di tingkat SMA/MA pada semester 2, materi ini sering kali dianggap siswa sebagai salah satu materi yang sulit untuk dipahami apalagi menyelesaikan soal-soalnya. Kesulitan yang dialami oleh siswa dalam menyelesaikan soal relativitas khusus einstein adalah bagaimana cara mengilustrasikan soal tentang penjumlahan kecepatan relativistik dan memasukkan besaran-besaran yang diketahui ke dalam rumus yang ada, kesulitan kedua yang dialami siswa dalam menyelesaikan soal relativitas khusus Einsten menentukan besarnya kecepatan v dari tetapan γ yang diketahui atau sebaliknya. Untuk yang kedua sih, mungkin banyak yang lebih kepada malas menghitung karena menggunakan persamaan yang cukup rumit.
Jurus jitu : menyelesaikan soal relativitas khusus einstein saya buat dengan maksud untuk sharing-sharing saja karena menurut saya cara ini bisa digunakan untuk membantu dalam memahami dan menyelesaikan soal tentang relativitas Einstein. Saya tidak mengklaim Jurus jitu (atau bisa disebut cara cepat, rumus cepat bebas lah) ini bukan berarti cara yang paling baik, mungkin diantara para pembaca ada yang memiliki cara yang lebih baik bisa di sharing di kolom komentar, serta jurus jitu ini bukan berarti cocok untuk digunakan oleh semua orang, karena pemahaman tiap orang pasti berbeda-beda, silahkan digunakan jika dirasa cocok jangan digunakan jika tak cocok. Sebelum membahas jurus jitu yang akan saja jabarkan, pertama-tama perlu diperhatikan beberapa konsep, untuk mengkroscek hasil perhitungan dengan teori yang ada.

Konsep 1 :
Tidak ada kecepatan yang melebihi kecepatan cahaya (c) yakni sebesar 3 x 10⁸ m/s. sehingga kecepatan tidak mungkin bernilai lebih dari c, seperti 1,1 c, 2 c¸ 3,2 c dst.
Konsep 2 :
Nilai γ selalu lebih besar dari pada 1 (γ > 1)
Jika dalam perhitungan hasilnya tidak sesuai dengan konsep di atas, silahkan dicek kembali rumus atau perhitungannya.

Jurus Jitu Pertama : menyelesaikan soal penjumlahan kecepatan relativistik

Persamaan umum untuk penjumlahan kecepatan relativistik adalah

Keterangan :
v_AB : kecepatan benda “A” terhadap benda “B”
v_AP : kecepatan benda “A” terhadap benda “P”
v_PB : kecepatan benda “P” terhadap benda “B”

Pada persamaan di atas saya menggunakan kata “benda” untuk menunjukkan objek yang diamati, akan tetapi pada soal biasanya objek dapat berupa pesawat, planet, elektron, peluru, dll. Perhatikan penulisan persamaan di atas selalu ada tiga buah kecepatan yakni satu kecepatan di ruas kiri (yang ditanyakan) dan dua kecepatan di sebelah kanan (yang diketahui), pada bagian indeksnya jika yang ditanyakan memiliki indeks “AB” maka penulisan indeks kecepatan pada ruas kanan harus “AP + PB”, jadi dapat kita katakan untuk “membentuk” indeks “AB” maka indeks penyusunnya adalah “AP + PB” atau bisa juga “A1 + 1B” dsb bergantung pada yang diketahui di soal, namun yang penting adalah bagian tengahnya harus sama. Dalam menyelesaikan soal tentang penjumlahan kecepatan relativistik ini, tidak terlalu sulit, beberapa hal yang perlu diperhatikan adalah

• Kecepatan adalah besaran vektor
Konsep dasar tentang kecepatan adalah bahwa kecepatan merupakan besaran vektor yang mana perlu memperhatikan arahnya. untuk dua benda yang bergerak searah maka kecepatannya sama-sama bernilai positif, sedangkan untuk dua benda yang bergerak berlawanan arah maka salah satu kecepatannya bernilai negatif dan yang lain bernilai positif
• Kecepatan adalah besaran vektor
Peng”indeks”an besaran kecepatan harus sesuai dengan soal, hal ini penting untuk dilakukan agar tidak salah dalam memasukkan ke dalam persamaan, serta dalam memberikan indeks saya pribadi tidak harus selalu menggunakan indeks “1, 2, A, atau B” pemberian indeks disesuaikan dengan soalnya.
Contoh :
Pesawat terbang A bergerak dengan kecepatan v relatif terhadap planet Bumi. Penulisan kecepatannya adalah v_AB
Sebuah peluru ditembakkan dari pesawat 1 dengan kecepatan sebesar v relatif terhadap pesawat 1. Penulisan kecepatannya adalah v_P1
• Sifat indeks
Sifat indeks yang dimaksudkan disini adalah jika penulisan indeksnya dibalik maka kecepatannya akan bernilai negatif, perhatikan contoh berikut ini.
v_AB = -v_BA
v_BP = -v_PB

untuk lebih memahami jurus jitu yang pertama ini, mari kita simak beberapa contoh soal berikut.

Contoh soal 1
Sebuah pesawat bergerak dengan kecepatan 0,6 c terhadap bumi. Dari pesawat ditembakkan peluru dengan kecepatan 0,4 c searah dengan gerak pesawat. Kecepatan peluru terhadap bumi adalah ….

pembahasan soal nomor 1:

Berdasarkan soal di atas, kita dapat mengetahui ada tiga buah objek yang diamati yakni pesawat (indeks “P”), peluru (indeks “R”), dan bumi (indeks “B”), gerakan ketiga objek tersebut dapat diilustrasikan sebagai berikut.

v_PB = 0,6c (kecepatan pesawat relatif terhadap bumi)
v_RP = 0,4c (kecepatan peluru relatif terhadap pesawat)
v_RB = ... ? (kecepatan peluru relatif terhadap bumi)
tuliskan persamaan umumnya sebagai berikut

(hasil kecepatannya tidak melebihi “c”)

Contoh Soal 2
Dua buah jet F16 Hornet dan F15 Tiger saling berpapasan, pengamat dibumi mengukur kecepatan jet F16 = 0,75 c dan jet F15 = 0,85 c. Tentukan kecepatan relatif jet F15 terhadap jet F16?

pembahasan soal nomor 2:

Berdasarkan soal di atas, kita dapat mengetahui ada tiga buah objek, yakni jet F16 Hornet (indeks “H”), jet F15 Tiger (indeks “T”) dan bumi (indeks “B”), gerakan ketiga objek tersebut dapat diilustrasikan sebagai berikut.

Perhatikan pertanyaannya, yakni kecepatan relatif jet F15 (Tiger) terhadap jet F16 (Hornet) sehingga penulisan indeks kecepatannya adalah v_TH.
v_HB = 0,75c (kecepatan pesawat F16 relatif terhadap bumi)
v_BH = -0,75c (ketika indeksnya di balik, maka akan bernilai negatif)
v_TB = -0,85c (kecepatan pesawat F15 relatif terhadap bumi)
tanda negatif, karena pesawat F15 Tiger bergerak ke kiri
v_TH = ... ? (kecepatan pesawat F15 relatif terhadap pesawat F16)
kita dapat menuliskan persamaan umumnya sebagai berikut

Tanda negatif menunjukkan pesawat F15 Tiger bergerak ke arah kiri relatif terhadap bumi (hasilnya kurang dari “c”)

Contoh soal 3
Pesawat angkasa Alfa berkecepatan 0,9 c terhadap bumi, jika pesawat Beta melewati pesawat Alfa dengan kecepatan relatif 0,5 c. Berapakah kecepatan pesawat Beta terhadap bumi?

pembahasan soal nomor 3:

Berdasarkan soal kita dapat mengetahui ada tiga objek yakni pesawat angkasa Alfa (indeks “A”, pesawat angkasa Beta (indeks “B”), dan bumi (indeks “P”). gerak ketiga pesawat tersebut dapat diilustrasikan sebagai berikut.

v_AP = 0,9c (kecepatan pesawat alfa terlatif terhadap bumi)
v_BA = 0,5c (kecepatan pesawat Beta relatif terhadap pesawat Alfa)
v_BP = ... ? (kecepatan pesawat Beta relatif terhadap bumi)
kita dapat menuliskan persamaan umumnya sebagai berikut

(hasil kecepatannya tidak melebihi “c”)

Jurus Jitu Kedua : hubungan antara kecepatan “v” dengan nilai “γ”

Dalam menganalisis gerak benda dengan kecepatan yang mendekati kecepatan cahaya, kita akan mengenal suatu nilai “γ” yang merupakan “faktor koreksi” dimana besarnya kecepatan ini dapat ditentukan dari kecepatan benda "v". nilai “γ” ini akan selalu ada ketika membahas soal tentang relativitas khusus Einstein baik itu terkait dengan massa, panjang, waktu, energi maupun momentum relativistik. Secara matematis hubungan antara kecepatan benda "v" dengan nilai “γ” dapat dilihat sebagai berikut.

Ketika melihat persamaan di atas, biasanya para siswa sudah berpikiran bahwa akan rumit penyelesaiannya sehingga menyebabkan rasa tidak ingin melanjutkan mengerjakan soal tersebut. sebagai contoh untuk benda yang bergerak dengan kecepatan 0,6c, nilai “γ” dapat ditentukan seperti berikut.

cara yang panjang seperti di atas sering kali membuat siswa sudah malas untuk mengerjakan soal. Nah pada kesempatan kali ini yang ingin saya share adalah salah satu cara atau teknik yang dapat digunakan untuk menentukan nilai “γ” dari kecepatan benda atau sebaliknya yakni dengan menggunakan konsep phytagoras.
Hubungan antara nilai “γ” dan kecepatan "v" dapat terlihat pada konsep phytagoras. Perhatikan gambar berikut untuk lebih jelasnya,

Konsep phytagoras sering digambarkan dalam segitiga siku-siku seperti gambar di atas yang terdiri dari tiga sisi yakni 2 sisi siku-siku dan satu sisi miring, segitiga siku-siku memiliki persamaan tersendiri yakni c² = a² + b² dengan c adalah sisi miring serta a dan b adalah sisi siku-sikunya. misalkan sebuah benda bergerak dengan kecepatan v = 0,6c, maka kita dapat menuliskannya dalam bentuk pecahan biasa v = 6/10 c, dimana pembilang (6) sebagai salah satu sisi siku-siku dan penyebut (10) sebagai sisi miringnya (perhatikan gambar garis kuning). pasangan sisi siku-siku lainnya kita misalkan “x” seperti terlihat pada gambar. nilai “γ” dalam bentuk pecahan disusun atas sisi miring sebagai pembilang (10) dan sisi siku-siku yang belum diketahui sebagai penyebut (x) , sehingga dengan menggunakan aturan phytagoras pasangan angka untuk triple phytagoras yang cocok adalah 6, 8, 10. Dengan demikian nilai “γ” dapat dengan mudah kita ketahui besarnya 10/8.
Teknik ini dapat kita gunakan untuk menyelesaikan berbagai permasalahan terkait dengan relativitas khusus Einstein, berikut disajikan tabel hubungan antara kecepatan v dengan nilai “γ” dengan menggunakan triple phytagoras.

Untuk lebih memahami jurus jitu yang kedua ini, perhatikan beberapa contoh soal dibawah ini.

Contoh soal 1
Pada saat bergerak, panjang sebuah pesawat menjadi setengah dari pesawat itu dalam keadaan diam. Jika c adalah kecepatan cahaya, maka kecepatan pesawat itu relatif terhadap pengamat yang diam adalah ….

pembahasan soal nomor 1:

Berdasarkan soal dapat diketahui,
L = ½ L₀
v ... ?
persamaan panjang relativistik benda adalah

Jika kita setarakan dengan soal, maka

Ingat dengan menggunakan konsep tripel phytagoras sisi miringnya adalah 2 dan satu sisi siku-sikunya adalah 1, maka sisi siku-siku lainnya dapat ditentukan dengan cara
c² = a² + b²
2² = 1² + x²
4 = 1 + x²
x² = 3
x = √3 panjang sisi siku-siku lainnya (sesuai dengan tabel di atas), sehingga kecepatan yang dimiliki oleh pesawat adalah v = ½ √3 c.

Contoh soal 2
Massa benda yang bergerak dengan kecepatan 0,8 c akan berubah menjadi n kali massa diamnya, maka n adalah ….

pembahasan soal nomor 2:

Berdasarkan soal dapat diketahui
v = 0,8 c
m = n m₀
n ... ?
persamaan untuk massa relativistik adalah
m = γ m₀
jadi pada dasarnya, n adalah nilai γ.
v = 0,8 c
v = 8/10 c
dimana:
10 adalah sisi miring
8 adalah salah satu sisi siku-siku,
Besarnya sisi siku-siku lainnya ditentukan dengan cara
c² = a² + b²
10² = 8² + x²
100 = 64 + x²
x² = 36
x = 6
jadi besar n atau nilai “γ” nya adalah
γ = 10/6

Contoh soal 3
Berapakah massa relativistik sebuah partikel (massa diam = 6 kg) yang bergerak dengan kelajuan 0,28 c?

pembahasan soal nomor 3:

Berdasarkan soal dapat diketahui
m₀ = 6 kg
v = 0,28 c
m ... ?
persamaan untuk massa relativistik adalah
m = γ m₀
sehingga kita menentukan nilai γ terlebih dahulu dengan cara sebagai beriku
v = 0,28 c = 7/25 c
pasangan tripel phytagoras untuk bilangan 7 dan 25 adalah 24 (lihat di tabel), sehingga nilai γ = 25/24
jadi massa relativistiknya
m = γ m0
m = 25/24 . 6
m = 25/4
m = 6,25 kg

Contoh soal 4
Agar energi kinetik benda bernilai 20% energi diamnya dan c adalah kelajuan cahaya dalam ruang hampa, maka benda harus bergerak dengan kelajuan ....

pembahasan soal nomor 4:

Berdasarkan soal dapat diketahui
EK = 20% E₀
v... ?
persamaan untuk energi relativisitik adalah
EK = (γ – 1) E₀
20% E₀ = (γ – 1) E₀
0,2 = γ – 1
γ = 1,2
γ = 12/10
dimana
12 merupakan sisi miring
10 merupakan salah satu sisi siku-siku
Untuk itu kita dapat menentukan sisi siku-siku yang lain dengan cara
c² = a² + b²
12² = 10² + x²
144 = 100 + x²
x² = 44
x = 2√11
sehingga benda harus bergerak dengan kecepatan

Demikian jurus jitu : menyelesaikan soal relativitas khusus Einstein yang bisa saya bagikan pada kesempatan kali ini, semoga bisa memberikan manfaat bagi para pembaca. jika ada saran-saran, kritik bisa dituliskan di kolom komentas