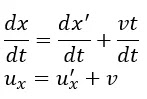Albert Einstein
(sumber : Fundamentals of Physics)
Albert Einstein seorang fisikawan asal Jerman yang sangat berpengaruh dalam perkembangan ilmu fisika, 1905 ketika ia berumur 25 tahun telah
mengemukakan sebuah teori yang terkenal dengan teori relativitas khusus. Disebut teori relativitas khusus, karena teori ini hanya berlaku untuk
kerangka acuan inersial (kerangka acuan yang diam atau bergerak dengan kecepatan konstan). Teori ini yang kemudian mengubah pandangan para
fisikawan terkait dengan konsep ruang dan waktu, menurut teori relativitas khusus ini ruang dan waktu tidak bersifat mutlak atau absolut
(tetap) tetapi bisa berubah jika bendanya bergerak dengan kecepatan yang mendekati kecepatan cahaya. Melalui teori relativitas khusus ini
ilmu fisika berkembang dengan pesat sehingga masa setelah di kemukakan teori ini oleh Einstein sering disebut fisika modern (masa sebelumnya
disebut dengan fisika klasik dimana benda bergerak dengan kecepatan jauh dibawah kecepatan cahaya, dengan Newton sebagai fisikawan paling populer
di masa ini).
Pada bab ini kita akan mempelajari bagaimana teori ini bisa muncul, fenomena apa yang tidak mampu dijelaskan oleh fisika klasik sehingga muncul teori
relativitas khusus, dan bagaimana penerapannya dalam kehidupan sehari-hari.
Relativitas Galileo
Dalam ilmu fisika, kita mengenal konsep gerak dimana gerak pada dasarnya bersifat relatif yang artinya gerak bergantung pada kerangka acuannya,
misalkan ketika kamu berhadap-hadapan dengan seorang teman, kemudian kamu melangkah ke kiri maka teman di hadapan kita akan beranggapan bahwa kita
bergerak ke kanan. Meskipun dikatakan geraknya berbeda (satu mengatakan ke kiri, satu mengatakan ke kanan) akan tetapi keduanya benar karena menggunakan
kerangka acuan yang berbeda, kamu mengatakan bergerak ke kiri dengan acuan dirimu sendiri, sedangkan temanmu yang berada di depanmu mengatakan kamu
bergerak ke kanan dengan kerangka acuan temanmu.
Selain gerak, kita juga harus memahami konsep kejadian. Kejadian dalam fisika merupakan suatu peristiwa fisika yang terjadi dalam suatu ruang dan
pada waktu tertentu, contohnya menyalakan lampu, tumbukan dua partikel, ledakan petasan, dll. Setiap kejadian fisika akan berada dalam koordinat
ruang dan waktu (spacetime coordinate) yang terdiri atas koordinat ruang (x, y, z) dan koordinat waktu (t). sistem koordinat itu sendiri juga merupakan
suatu kerangka acuan. Seseorang yang mengamati suatu kejadian fisika dan melakukan pengukuran disebut pengamat, perlu dipahami bahwa untuk satu
kejadian dapat diamati oleh lebih dari satu pengamat jika sistem koordinat yang dipakai masing-masing pengamat berbeda juga.
Berdasarkan penjelasan di atas, teori relativitas erat kaitannya dengan kejadian-kejadian yang teramati dari kerangka acuan inersial, yang mana
kerangka acuan juga tidak bersifat mutlak. Oleh Galileo mengemukakan prinsip relativitas Galileo (di beberapa buku ada yang menyebutkan prinsip
relativitas Newton) yakni
Hukum-hukum mekanika berlaku sama untuk semua kerangka acuan inersial
Untuk lebih memahami prinsip relativitas Galileo ini perhatikan ilustrasi berikut.
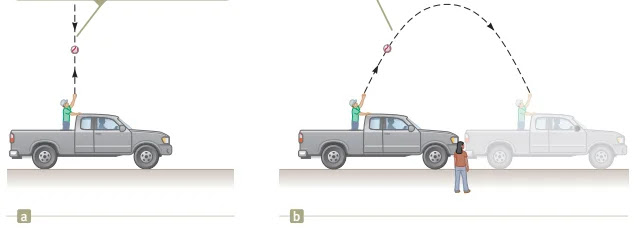
Gambar 1. Dua pengamat sedang mengamati lintasan bola ketika dilempar ke atas kemudian jatuh kembali, ternyata menghasilkan dua lintasan yang berbeda
(sumber: physics for scientists and engineers with modern physics)
Sebuah truk yang bergerak dengan kecepatan konstan terhadap bumi dengan seorang penumpang di bak belakang (gambar 1a). Jika penumpang yang berada
di belakang truk melemparkan bola ke atas kemudian ditangkap kembali ketika jatuh, hasil pengamatan orang tersebut adalah bahwa lintasan yang ditempuh
oleh bola tersebut berupa garis lurus vertikal, hal ini dikarenakan ia juga ikut bergerak bersama dengan truk (bola hanya memiliki kecepatan dalam arah
sumbu y tidak memiliki kecepatan dalam arah sumbu x). Akan tetapi jika ada orang diam di pinggir jalan (gambar 1b) mengamati lintasan yang ditempuh oleh
bola tersebut akan menghasilkan bahwa lintasan yang ditempuh oleh bola berupa lintasan parabola, hal ini dikarenakan menurut orang yang diam dipinggir
jalan selain bola bergerak secara vertikal bola juga bergerak secara horizontal (bola memiliki kecepatan searah sumbu y dan sumbu x). Dalam kerangka
acuan yang berbeda (pengamat di atas bak truk dan pengamat diam di pinggir jalan) hukum – hukum mekanika berlaku untuk kedua kerangka acuan tersebut
meskipun menghasilkan lintasan yang berbeda.
Transformasi Galileo
Berdasarkan ilustrasi di atas, kita mengetahui bahwa dalam satu kejadian bisa diamati dari dua kerangka acuan yakni kerangka acuan yang diam
(orang diam di pinggir jalan) dan kerangka acuan yang bergerak (orang berada di atas bak truk).
Suatu kejadian dalam fisika terjadi dalam sistem koordinat 4 dimensi yakni koordinat ruang dan waktu (x, y, z, t) serta bisa diamati dari dua kerangka kejadian,
hubungan antara kedua kerangka acuan dan kejadian tersebut dapat dijelaskan menggunakan kerangka acuan inersial dalam satu gambar seperti berikut.
Gambar 2. Kejadian yang terjadi pada titik P. Kejadian ini di amati dari dua kerangka acuan yakni S dan S’, dimana S’ bergerak dengan kecepatan v relatif terhadap S.
Berdasarkan dua sistem koordinat S dan S’ (gambar 2), dimana S’ bergerakan dengan kecepatan konstan v terhadap S searah dengan sumbu x dan x’
(keduanya berhimpit). Dalam hal ini kita asumsikan bahwa pada awalnya kedua kerangka acuan berhimpit (saat t = t’ = 0) dan kejadian pada titik P terjadi dalam ruang dan waktu yang bersamaan ditinjau dari kedua sistem koordinat (t=t’). Pengamat berada pada titik O untuk sistem koordinat S (x, y, z, t) dan pengamat pada titik O’ untuk sistem koordinat S’ (x’, y’, z’, t’). Gambar 2, menunjukkan bahwa kerangka acuan S’ hanya
bergerak terhadap sumbu x sehingga dengan menggunakan analisis geometri kita dapat menuliskan hubungan jarak kejadian terhadap kedua sistem koordinat tersebut sebagai berikut
x = x’ + vt, y = y’, z = z’, t = t’
persamaan di atas kita sebut sebagai transformasi Galileo untuk koordinat ruang dan waktu. Perhatikan bahwa waktu diasumsikan sama untuk kedua sistem koordinat. Sehingga
perubahan waktu yang terjadi untuk sistem koordinat S sama dengan perubahan waktu yang terjadi untuk sistem koordinat S’.
Jika titik P berpindah dalam arah sumbu x sebesar dx dalam selang waktu dt yang diamati dari kerangka acuan S, pada saat yang sama jika di amati dari kerangka acuan S’ maka titik P akan mengalami perpindahan sejauh dx’ maka kecepatan titik P
terhadap kerangka acuan S dan S’ dapat kita tentukan dengan menurunkan fungsi perpindahan terhadap waktu seperti berikut ini.
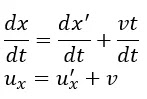
Dimana v merupakan kecepatan kerangka acuan S’ terhadap kerangka acuan S, dengan cara yang sama maka kita dapat memperoleh kecepatan titik P terhadap
sumbu y yakni u’y = uy dan
kecepatan titik P terhadap sumbu z yakni u’z = uz. secara lengkap transformasi galilleo untuk kecepatan adalah sebagai berikut
ux = ux’ + v, u’y = uy, u’z = uz
kecepatan cahaya
Diakhir tahun 1800, para fisikawan berpendapat bahwa, sekitar tahun 1964 seorang fisikawan dari MIT melakukan sebuah eksprimen untuk mempercepat
gerak elektron dengan cara memberikan gaya tolak kepada elektron tersebut. berdasarkan hasil percobaannya ternyata di menemukan bahwa gaya yang bekerja
pada elektron yang bergerak sangat cepat bertambah besar, maka energi kinetik elektron juga semakin besar, tetapi kecepatannya tidak bertambah secara
signifikan (perhatikan gambar 3).
Gambar 3. Titik pada grafik merupakan besarnya energi kinetik yang dimiliki oleh sebuah elektron terhadap kecepatannya. tidak peduli berapa besar energi yang diberikan kepada elektron (atau partikel lain yang bermassa), kecepatannya tidak pernah sama atau mencapai kecepatan mutlak “c”.
(sumber : “Fundamentals of Physics”)
Elektron yang dipercepat dalam laboratorium sekitar 0,999 999 999 95 kali kecepatan cahaya tetapi kecepatannya tetap di bawah kecepatan cahaya sebesar c.
sehingga kecepatan cahaya disebut dengan kecepatan mutlak, dimana nilai c = 3 x 108 m/s . Hasil percobaan di atas juga menunjukkan bahwa
tidak ada benda yang bisa bergerak melebihi kecepatan cahaya, hal ini tidak sesuai jika kita menggunakan transormasi Galileo. Perhatikan ilustrasi berikut.
Gambar 4. Sebuah pesawat yang begerak dalam kerangka acuan “A” yang juga bergerak dengan kecepatan konstan “v”
(sumber : Physics – Course Companion)
Sebuah pesawat luar angkasa yang begerak dengan kecepatan 0,7c dalam kerangka acuan A yang juga bergerak dengan kecepatan
0,6c searah dengan arah gerak pesawat. Jika seorang melihat dari bumi yang diam, maka berdasarakan transformasi Galileo kecepatan pesawat tersebut adalah
vp = uA + v
vp = 0,7c + 0,6c
vp = 1,3c
kecepatan pesawat tersebut tidak mungkin terjadi, karena tidak ada benda yang bergerak melebihi kecepatan cahaya. Hal ini merupakan kelemahan dari tranformasi Galileo.
Tranformasi Lorentz
Untuk menjawab permasalahan di atas, maka diperlukan suatu faktor koreksi yang mampu menyelesaikan fenomena di atas tanpa menyalahi hasil
eksperimen. Faktor koreksi ini disebut dengan Faktor Lorentz yakni

Bentuk transformasi Lorentznya adalah sebagai berikut
x = γ(x’ + vt), y = y’, z = z’, t’ = γ(t + vx/c2)
Tranformasi Lorentz untuk kecepatan dapat diturunkan
Jika kita bagi persamaan (1) dan (2) maka
gambar 4c
Persamaan di atas masih mengikuti pada gambar 2 dengan
v’
x = kecepatan benda pada kerangka acuan S’
v
x = kecepatan benda pada kerangka acuan S
v = kecepatan S’ relatif terhadap S
untuk lebih memahami persamaan tersebut, perhatikan ilustrasi berikut ini!
Gambar 5. Dua pesawat yang bergerak di sekitar planet
Misalkan kita diminta untuk menentukan besar kecepatan pesawat A relatif terhadap planet maka perumusannya dapat ditulis
Penting untuk dipahami dalam memaknai persamaan di atas, pertama Dalam penulisan kecepatan perhatikan indeksnya
v
AP merupakan kecepatan pesawat “A” terhadap planet
v
AB merupakan kecepatan pesawat “A” terhadap pesawat “B”
v
BP merupakan kecepatan pesawat “B” terhadap Planet
perhatikan pula peletakaan indeks pada bagian atas dari persamaan
Jika dalam penulisan awalnya indeks terbalik dengan yang ada di dalam persamaan, maka ketika memasukkan nilainya diberikan tanda negatif, b
egitu pula jika kedua benda begerak berlawan arah, maka salah satunya juga dibuat negatif (ingat kecepatan adalah besaran vektor). Mari kita
lanjutan pembahasan ini dengan menerapkannya dalam beberapa soal seperti berikut.
Latihan soal 1Sebuah pesawat ruang angkasa bergerak dengan kecepatan 0,6c meninggalkan bumi. Dari pesawat tersebut ditembakkan peluru dengan kecepatan 0,5c (c = kecepatan cahaya di ruang hampa). Berapa kecepatan peluru menurut pengamat di Bumi jika arah peluru searah pesawat ....
A. 0,75c
B. 0,85c
C. 0,95c
D. 0,88c
E. 0,55c
Kunci jawaban : “B”
Latihan soal 2
Dua benda bergerak dengan arah yang berlawanan dan kecepatan masing-masing ½ c dan ¼ c. Jika c = kecepatan cahaya, maka kecepatan benda pertama terhadap benda kedua sebesar ....
A. 0,750 c
B. 0,666 c
C. 0,500 c
D. 0,125 c
E. 0,250 c
Kunci jawaban : “B”
Latihan soal 3
Pesawat angkasa Alfa berkecepatan 0,9 c terhadap bumi, jika pesawat Beta melewati pesawat Alfa dengan kecepatan relatif 0,5 c. Berapakah kecepatan pesawat Beta terhadap bumi?
Kunci jawaban : “0,97c”
Latihan soal 4
Sebuah pesawat antariksa bergerak dengan kelajuan 0,85 c. seorang anak dalam pesawat tersebut menembakkan rudal dengan kelajuan 0,35 c searah dengan gerak pesawat.kecepatan rudal tersebut menurut pengamat di bumi jika berdasarkan relativitas Einstein adalah…
a. 0,48c
b. 0,82c
c. 0,88c
d. 0,92c
e. 0,99c
Kunci jawaban : “D”
Latihan soal 5
Dua pesawat antariksa A dan B bergerak dengan arah berlawanan, seorang pengamat di bumi mengukur kelajuan pesawat A sebesar 0,75c dan kelajuan pesawat B adalah 0,85c. kelajuan pesawat A relative terhadap pengamat di bumi adalah…
a. 0,81c
b. 0,88c
c. 0,98c
d. 0,99c
e. 1,23c
Kunci jawaban : “C”
demikian sekilas pembahasan pada kali ini, semoga bermanfaat bagi para pembaca