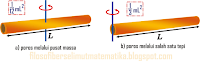
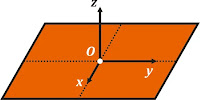
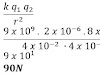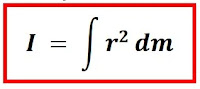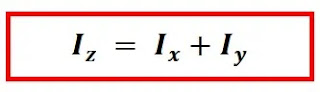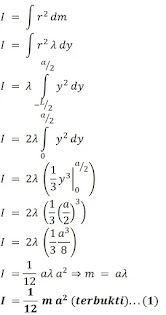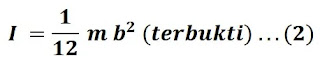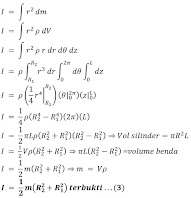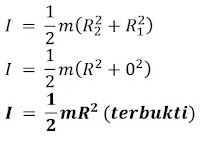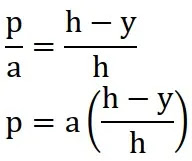) maka kita dapat menggunakan teorema sumbu sejajar untuk menemukan momen inersianya, dimana sumbu poros bergeser sejauh ½ L
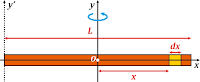
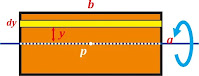
Berdasarkan gambar di atas, maka dapat kita ketahui bahwa momen inersia pada sumbu
y sama dengan momen inersia pada pers (1) dan momen inersia pada sumbu
x sama dengan momen inersia pada pers (2) sehingga dapat kita tuliskan
I
z = I
x + I
y
I
z = 1/12 mb
2 + 1/12 ma
2
Iz = 1/12 m (a2 + b2) (terbukti)
Poros sepanjang tepi (salah satu sisinya)
Momen inersia pelat sepanjang tepi salah satu sisinya dapat ditentukan dengan menggunakan teorema sumbu sejajar, dimana poros sejajar dan bergeser sejauh ½ a dari poros dipusat massanya (pers. 2), maka dapat kita tuliskan
I = I
pm + md
2
I = 1/12 ma
2 + m( ½a)
2
I = 1/12 ma
2 + ¼ ma
2
I = 1/12 ma
2 + 3/12 ma
2
I = 4/12 ma
2
I = 1/3 ma2 (terbukti)
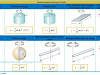
Silinder
Silinder berongga
Sebuah silinder yang bermassa m dan panjang L memiliki lubang di tengah-tengahnya dengan jari-jari seperti tampak pada gambar a. jika silinder tersebut berotasi dengan sumbu poros melalui pusat massanya, maka momen inersianya dapat ditentukan sebagai berikut
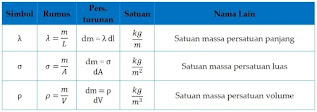
dm = ρ dV
dm = ρ r dr dθ dz (sistem koordinat silinder)
dengan batas integrasi
r : R1 sampai R2
θ : 0 sampai 2π
z : 0 sampai L
Sehingga
Silinder pejal
Momen inersia silinder pejal dapat ditentukan ketika nilai R1 pada persamaan (3) sama dengan nol dan R2 sama dengan R (jari-jari silinder), sehingga dapat ditulis
Silinder tipis berongga
Momen inersia silinder tipis berongga dapat ditentukan ketika nilai R1 = R2 = R, silinder hanya memiliki kulit tipis. Maka persamaan (3) dapat ditulis.
Bola
Bola pejal dengan poros melalui pusat massa
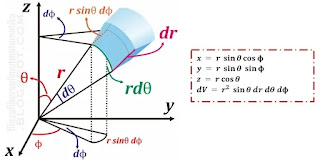
Momen inersia bola pejal dengan poros melalui pusat massa, dapat ditentukan dengan menggunakan sistem koordinat bola sehingga elemen massanya dapat ditulis sebagai berikut
dm = ρ dV
dm = ρ r
2 sin θ dr dθ dϕ (koordinat bola)
r = r sin θ
dengan batas integrasi
r : 0 sampai R
θ : 0 sampai π
ϕ : 0 sampai 2π
Sehingga
Bola pejal dengan poros di tepi
Momen inersia bola pejal dengan poros di tepi dapat ditentukan dengan teorema sumbu sejajar dengan poros bergeser sejauh R dari poros pusat massanya, sehingga
I = Ipm + md
2
I = 2/5 mR
2 + m(R)
2
I = 2/5 mR
2 + mR
2
I = 7/5 mR2 (terbukti)
Bola tipis berongga
Momen inersia bola tipis berongga yang dimaksudkan disini adalah sebuah bola yang terlapisi oleh sebuah kulit tipis (seperti bola pingpong), maka dalam menentukan nilai elemen massa
(dm) tidak menggunakan volume akan tetapi luas permukaan bola.
dm = σ r
2 sin θ dθ dϕ dA
r = r sin θ
dengan batas integrasi
θ : 0 sampai π
ϕ : 0 sampai 2π
sehingga
Ekstra TIme
Segitiga
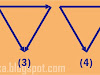
Sebuah segitiga sama sisi yang memiliki panjang sisi sebesar a diputar dengan poros berada pada satu sisi, tampak seperti gambar berikut
Elemen massa diambil lebar
dy dan berjarak
y dari sumbu poros. Karena nilai
p berubah untuk setiap perubahan
y maka, nilai
p dapat ditentukan dengan persamaan
dm = σ dA (dA = p dy)
dm = σ p dy
r = y
dengan batas integrasi
y : 0 sampai h
sehingga
Kerucut
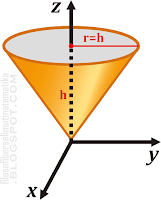
Tentukan momen inersia sebuah kerucut yang memiliki tinggi
h sama dengan jari-jari alasnya
r (h=r) yang diputar dengan sumbu poros
z tampak seperti gambar berikut
Untuk menentukan momen inersia kerucut di atas, pertama-tama perlu diketahui bahwa kerucut tersebut terbentuk dengan menarik luasan alas (lingkaran) dari
z = 0 sampai
z = h. Setiap perubahan h jari-jarinya juga berubah dari
r = 0 sampai
r = h, sehingga dapat dikatakan batas untuk jari-jari tersebut adalah dari
r = 0 sampai
r = z. Selain itu, kita harus menggunakan sistem koordinat silinder untuk menentukan elemen massanya yang dapat dituliskan
dm = ρ r dr dθ dz
r = r
dengan batas integrasi
r : 0 sampai z
θ : 0 sampai 2π
z : 0 sampai h
sehingga
Demikian penurunan rumus momen inersia untuk berbagai benda, semoga dapat menambah pengetahuan para pembaca dan tidak membingungkan. Jika ada kritik dan saran bisa tinggalkan komentarnya di bawah.Agar pemahamannya lebih lengkap perlu diketahui Materi ini hanya sebagian dari
materi fisika dinamika rotasi