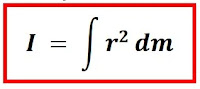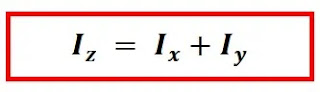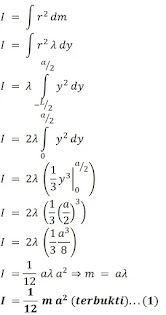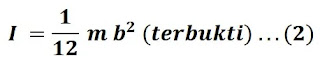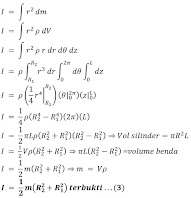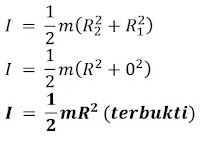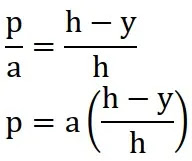Praktikum fisika : hukum Coulomb dengan memanfaatkan lab virtual ini merupakan salah satu variasi pembelajaran Di masa pandemi seperti sekarang yang pembelajaran lebih banyak dilakukan secara daring atau istilahnya PJJ (pembelajaran jarak jauh). Berdasarkan pengamatan penulis, PJJ lebih banyak dilakukan dengan memberikan materi dan mengerjakan soal. Berikut bentuk LKS yang telah dibuat. Semoga bermanfaat
Minggu, 20 September 2020
Jumat, 18 September 2020

soal latihan SMA
| 19.17
Latihan soal dan pembahasan : Medan magnet (materi fisika kelas 12)
Medan magnet merupakan salah satu materi fisika yang dipelajari di kelas 12
semester 1, oleh karena itu disini saya mencoba untuk membuat latihan soal materi
medan magnet beserta pembahasannya secara terperinci, bisa dijadikan latihan untuk
para siswa agar lebih memahami materi medan magnet atau referensi oleh guru
dalam membuat soal ulangan. Soal yang disajikan memiliki banyak tipe soal yang
diambil dari soal-soal ujian masuk atau UN sehingga cocok untuk dibuat belajar
menjelang ulangan harian atau akan mengikuti tes, untuk materi medan magnet silahkan mengunjungi postingan berikut. Selamat menikmati
Soal pilihan ganda
Soal pilihan ganda
Kamis, 10 September 2020

soal latihan SMA
| 07.15
Latihan Soal dan pembahasan lengkap materi : Elastisitas (fisika kelas 11)
Elastisitas merupakan salah satu materi fisika yang dipelajari di kelas 11 semester 1,
oleh karena itu disini saya mencoba untuk membuat latihan soal dan pembahasan lengkap tentang materi fisika elastisitas, bisa dijadikan latihan untuk para
siswa agar lebih memahami materi elastisitas atau referensi oleh guru dalam
membuat soal ulangan. Soal yang disajikan memiliki banyak tipe soal yang diambil
dari soal-soal ujian masuk atau UN sehingga cocok untuk dibuat belajar menjelang
ulangan harian atau akan mengikuti tes. Sebelum melanjutkan membaca latihan soal
ini, ada baiknya membaca dulu konsep rahasia perbandingan karena itu merupakan
salah satu konsep yang sangat berguna dalam menyelesaikan latihan soal tentang
materi fisika elastisitas ini. Selamat menikmati
Rabu, 02 September 2020

soal latihan SMA
| 07.49
Latihan soal dan pembahasan lengkap : Gerak Parabola (materi fisika kelas 10)
Gerak parabola merupakan salah satu materi fisika yang dipelajari di kelas 10 semester 1, tidak sedikit siswa yang merasa kurang memahami materi ini terutama ketika disajikan soal-soal yang aplikatif, menggunakan persamaan yang lebih banyak, dan konsep matematis yang cukup kompleks oleh karena itu disini saya mencoba untuk membuat latihan soal tentang materi fisika gerak parabola beserta pembahasannya secara terperinci, bisa dijadikan latihan untuk para siswa agar lebih memahami materi listrik statis atau referensi oleh guru dalam membuat soal ulangan. Soal yang disajikan memiliki banyak tipe soal yang diambil dari soal-soal ujian masuk atau UN sehingga cocok untuk dibuat belajar menjelang ulangan harian atau akan mengikuti tes. Pembahasan yang saya tulis disini tidak selalu menggunakan “rumus jadi” untuk gerak parabola seperti mencari tmax, hmax, atau xmax tapi saya juga menggunakan rumus-rumus dasar dari gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB) yang sudah dipelajari pada bab sebelumnya.
Selasa, 25 Agustus 2020
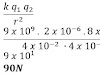
soal latihan SMA
| 16.13
Latihan soal fisika dengan pembahasan lengkap materi: Listrik Statis (part 1)
Listrik statis merupakan salah satu materi fisika yang dipelajari di kelas 12 semester 1, tidak sedikit siswa yang merasa kurang memahami materi ini terutama ketika disajikan soal-soal yang aplikatif, oleh karena itu disini saya mencoba untuk membuat latihan soal tentang materi fisika listrik statis beserta pembahasannya secara terperinci, bisa dijadikan latihan untuk para siswa agar lebih memahami materi listrik statis atau referensi oleh guru dalam membuat soal ulangan. Soal yang disajikan memiliki banyak tipe soal yang diambil dari soal-soal ujian masuk atau UN sehingga cocok untuk dibuat belajar menjelang ulangan harian atau akan mengikuti tes. Sebelum melanjutkan membaca latihan soal ini, ada baiknya membaca dulu konsep rahasia perbandingan untuk menyelesaikan soal fisika karena itu merupakan salah satu konsep yang sangat berguna dalam menyelesaikan latihan soal tentang materi fisika listrik statis ini. Selamat menikmati
Senin, 17 Agustus 2020
soal latihan kelas 10
| 13.08
Latihan soal dan pembahasan : vektor (Materi fisika kelas 10)
Salah satu materi fisika kelas 10 SMA pada semester 1 adalah tentang vektor, materi ini adalah materi dasar yang sangat penting di fisika. Besaran vektor akan sering ditemui dalam berbagai bab yang lain, oleh karena itu setelah kemarin saya upload ringkasan materi tentang vektor kali ini saya menyajikan latihan soal berserta pembahasannya secara lengkap dan terperinci terkait tentang materi vektor yang bisa digunakan untuk pendalaman materi atau soal-soal ulangan harian. dalam pengerjaan soal fisika akan lebih mudah jika sudah memahami rahasia konsep perbandingan, karena konsep ini sangat diperlukan untuk menyelesaikan soal-soal aljabar Selamat menikmati.
Selasa, 11 Agustus 2020
soal latihan kelas 11
| 16.45
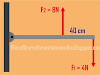
Latihan soal fisika materi : Dinamika Rotasi (Pembahasan Lengkap)
Salah satu materi fisika kelas 11 adalah tentang dinamika rotasi, banyak siswa yang merasa kesulitan untuk mengerjakan soal tentang dinamika rotasi ini terutama terkait dengan hubungan torsi dengan gerak menggelinding, menentukan momen inersia, atau energi kinetik benda saat menggelinding. Berikut ini adalah beberapa contoh latihan soal materi fisika kelas 11 tentang dinamika rotasi lengkap dengan pembahasannya, dapat juga digunakan sebagai refrensi untuk soal ulangan harian. Semoga bisa membantu dan selamat menikmati
Tips :
ketentuan untuk momen gaya yang searah jarum jam bernilai negatif dan untuk momen gaya berlawanan arah jarum jam bernilai positif.
Rabu, 05 Agustus 2020

Materi SMA
| 11.18
Materi fisika kelas 10 : vektor (Lengkap dengan contoh soal)
Daftar IsiMateri fisika kelas 10 : vektor (Lengkap dengan contoh soal)
Gambar 1. Papan penunjuk jalan
Gambar 1 di atas merupakan salah satu tanda yang sering kita lihat ketika
bepergian yang digunakan agar orang yang melintasi jalan tersebut tidak
tersesat dan bisa sampai ke tujuan dengan benar. Papan tersebut pada dasarnya
menunjukkan arah ke mana kita harus pergi, mengetahui arah merupakan sesuatu
yang sangat penting dalam kehidupan sehari-hari, bayangkan Orang yang sedang
bepergian akan kesulitan menuju tempat tujuannya jika tidak ada penunjuk jalan
yang menunjukkan arahnya. Dalam pembelajaran fisika materi tentang arah
termasuk dalam materi kelas 10 yakni “vektor” membahas tentang besaran-besaran
fisika yang memiliki arah. Pentingnya “arah” memang tak dapat dipungkiri lagi
bagi kehidupan sehari-hari tanpa adanya arah kita akan kesulitan untuk
mengetahui posisi kita dan posisi tujuan kita, dengan mengetahui arah kita
tidak akan tersesat. bahkan jika tidak ada arah mungkin tidak akan ada yang
namanya GPS “global positioning system” karena pada dasarnya GPS
menggunakan sistem koordinat untuk posisi kita dan posisi tujuan sehingga
dapat menemukan arah yang tepat untuk menuju lokasi tujuan tersebut. Oleh
karena itu setelah mengetahui manfaat “arah” dalam kehidupan sehari-hari,
silahkan mempelajari materi berikut ini.
Rabu, 29 Juli 2020
Materi kelas XI
| 09.41
Penurunan rumus momen inersia berbagai benda (lengkap dengan penjelasannya)
- Konsep rapat massa
- Sistem koordinat silinder dan sistem koordinat bola
- Teorema sumbu sejajar
- Teorema sumbu tegak lurus
- Penurunan rumus momen inersia berbagai benda
- Ekstra TIme
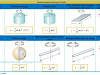
Gambar 1. Momen inersia berbagai benda
Saat mempelajari materi dinamika rotasi, tentu kalian pernah melihat gambar di atas ,Tapi pernahkah kalian berpikir asal dari persamaan-persamaan di atas? Berdasarkan hasil literasi dari berbagai sumber yang ada , Pada kesempatan kali ini saya akan mencoba melakukan penurunan rumus momen inersia untuk berbagai benda di atas sehingga ditemukan rumus-rumus dan angka di atas.
Penurunan rumus momen inersia untuk berbagai benda di atas, pada dasarnya menggunakan persamaan umum momen inersia yang sudah pernah saya bahas di metari dinamika rotasi untuk kelas 11 yakni
Persamaan di atas, merupakan persamaan dasar untuk semua jenis benda dengan massa yang terdistribusi kontinu, selain itu juga diperlukan konsep-konsep pendukung agar persamaan tersebut dapat menghasilkan rumus momen inersia untuk berbagai benda. Salah satu konsep matematis dasar yang perlu dipahami dalam menganalisis persoalan fisika adalah konsep perbandingan selain itu, Beberapa konsep lain khusus pembahasan ini yang menurut saya perlu dipahami antara lain
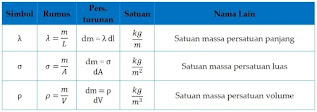
Konsep rapat massa
Konsep rapat massa yang saya maksudkan disini adalah kerapatan massa terhadap suatu besaran lain yakni rapat massa terhadap panjang (biasa disebut dengan satuan massa persatuan panjang). Ada tiga rapat massa yang perlu dipahami disini seperti yang ditunjukkan tabel berikut.Konsep rapat massa ini digunakan untuk mensubstitusi nilai “dm” pada persamaan umum di atas, perhatikan juga jenis bendanya (1 dimensi, 2 dimensi, atau 3 dimenssi).
Sistem koordinat silinder dan sistem koordinat bola
Koordinat silinder dan koordinat bola sangat penting untuk dipahami, karna sebagian besar benda yang akan diturunkan rumus momen inersianya adalah benda-benda dengan bentuk silinder dan bola seperti: silinder pejal, silinder berongga, bola pejal, bola berongga dll. benda-benda tersebut akan lebih mudah dianalisis menggunakan sistem koordinat silinder dan sistem koordinat bola. Berikut gambar dan transformasi kedua sistem tersebutSistem koordinat silinder
Gambar 2. Koordinat silinder
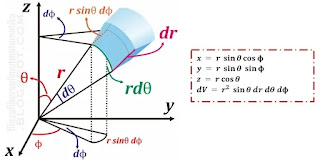
Sistem koordinat bola
Gambar 3. Koordinat bola
Teorema sumbu sejajar
Teorema sumbu sejajar dapat digunakan untuk menentukan momen inersia suatu benda ketika sumbu porosnya tidak terletak pada pusat massa tetapi sejajar dengan sumbu poros melalui pusat massanya, teorema untuk sudah saya bahas di materi dinamika rotasi. Secara matematis dapat ditulisTeorema sumbu tegak lurus
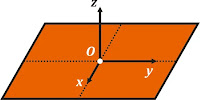
Teorema sumbu tegak lurus artinya sumbu poros yang tegak lurus sumbu melalui pusat massa yang tegak lurus penampang. Teorema ini memungkinkan menentukan momen inersia ketika sumbu porosnya tegak lurus penampang (sumbu z)dengan memanfaatkan momen inersia untuk poros tegak lurus lainnya (terhadap sumbu x dan sumbu y). Perhatikan gambar berikut
Gambar 4. Teorema sumbu tegak lurus
Iz = ∫ r2 dm
Iz = ∫ (x2 + y2) dm
Iz = ∫ x2 dm + ∫ y2 dm
Penurunan rumus momen inersia berbagai benda
Berikut penurunan rumus momen inersia berbagai bendaBatang silinder pejal
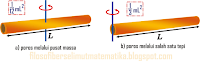
Poros melalui titik pusat massanya
Perhatikan gambar berikut, untuk mempermudah menurunkan rumusnya
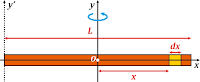
Batang yang bermassa m dan memiliki panjang L dengan pusat massa berada di titik O (berada di sumbu y), tampak seperti gambar di atas. Tentukan terlebih dahulu elemen massanya (kotak warna kuning) yang memiliki ukuran dx dan berjarak x dari pusat massanya.
dm = λ dx
r = x
dengan batas integrasi
x : - ½ L sampai ½ L
sehingga
dm = λ dx
r = x
dengan batas integrasi
x : - ½ L sampai ½ L
sehingga
Poros melalui salah satu ujung
Perhatikan kembali gambar di atas, jika sumbu poros di geser ke tepi (sumbu y’) maka kita dapat menggunakan teorema sumbu sejajar untuk menemukan momen inersianya, dimana sumbu poros bergeser sejauh ½ LI = Ipm + md2
I = 1/12 mL2 + m( ½L)2
I = 1/12 mL2 + ¼ mL2
I = 1/12 mL2 + 3/12 mL2
I = 4/12 mL2
I = 1/3 mL2 (terbukti)
Pelat tipis
Poros sepanjang tepi (salah satu sisinya)
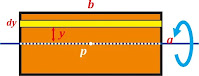
Perhatikan gambar berikutPlat tipis yang bermassa m dan memiliki panjang dan lebar berturut-turut adalah b dan a. Jika pelat tersebut diputar dengan poros sejajar salah satu sisi (b) melewati titik pusat massanya (p), maka untuk menentukan momen inersianya pertama-tama kita tentukan terlebih dahulu elemen massa dm yang memiliki panjang b dan lebar dy terletak sejauh y dari poros yang tampak seperti gambar di atas. Sehingga dapat kita tulis dm = λ dy
r = y
dengan batas integrasi
y : - ½ a sampai ½ a
sehingga
Dengan cara yang sama kita dapat menentukan momen inersia ketika porosnya sejajar dengan sisi a dan melewati titik pusat massanya yakni sebesar
Poros di pusat massanya dan tegak lurus bidang
Momen inersia pelat dengan sumbu poros di pusat massanya dan tegak lurus lurus bidang dapat ditentukan dengan menggunakan teorema sumbu tegak lurusBerdasarkan gambar di atas, maka dapat kita ketahui bahwa momen inersia pada sumbu y sama dengan momen inersia pada pers (1) dan momen inersia pada sumbu x sama dengan momen inersia pada pers (2) sehingga dapat kita tuliskan
Iz = Ix + Iy
Iz = 1/12 mb2 + 1/12 ma2
Iz = 1/12 m (a2 + b2) (terbukti)
Poros sepanjang tepi (salah satu sisinya)
Momen inersia pelat sepanjang tepi salah satu sisinya dapat ditentukan dengan menggunakan teorema sumbu sejajar, dimana poros sejajar dan bergeser sejauh ½ a dari poros dipusat massanya (pers. 2), maka dapat kita tuliskanI = Ipm + md2
I = 1/12 ma2 + m( ½a)2
I = 1/12 ma2 + ¼ ma2
I = 1/12 ma2 + 3/12 ma2
I = 4/12 ma2
I = 1/3 ma2 (terbukti)
Silinder
Silinder berongga
Sebuah silinder yang bermassa m dan panjang L memiliki lubang di tengah-tengahnya dengan jari-jari seperti tampak pada gambar a. jika silinder tersebut berotasi dengan sumbu poros melalui pusat massanya, maka momen inersianya dapat ditentukan sebagai berikut
dm = ρ dV
dm = ρ r dr dθ dz (sistem koordinat silinder)
dengan batas integrasi
r : R1 sampai R2
θ : 0 sampai 2π
z : 0 sampai L
Sehingga
dm = ρ r dr dθ dz (sistem koordinat silinder)
dengan batas integrasi
r : R1 sampai R2
θ : 0 sampai 2π
z : 0 sampai L
Sehingga
Silinder pejal
Momen inersia silinder pejal dapat ditentukan ketika nilai R1 pada persamaan (3) sama dengan nol dan R2 sama dengan R (jari-jari silinder), sehingga dapat ditulisSilinder tipis berongga
Momen inersia silinder tipis berongga dapat ditentukan ketika nilai R1 = R2 = R, silinder hanya memiliki kulit tipis. Maka persamaan (3) dapat ditulis.Bola
Bola pejal dengan poros melalui pusat massa
Momen inersia bola pejal dengan poros melalui pusat massa, dapat ditentukan dengan menggunakan sistem koordinat bola sehingga elemen massanya dapat ditulis sebagai berikut
dm = ρ dV
dm = ρ r2 sin θ dr dθ dϕ (koordinat bola)
r = r sin θ
dengan batas integrasi
r : 0 sampai R
θ : 0 sampai π
ϕ : 0 sampai 2π
Sehingga
I = Ipm + md2
I = 2/5 mR2 + m(R)2
I = 2/5 mR2 + mR2
I = 7/5 mR2 (terbukti)
dm = σ r2 sin θ dθ dϕ dA
r = r sin θ
dengan batas integrasi
θ : 0 sampai π
ϕ : 0 sampai 2π
sehingga
Elemen massa diambil lebar dy dan berjarak y dari sumbu poros. Karena nilai p berubah untuk setiap perubahan y maka, nilai p dapat ditentukan dengan persamaan
dm = σ dA (dA = p dy)
dm = σ p dy
r = y
dengan batas integrasi
y : 0 sampai h
sehingga
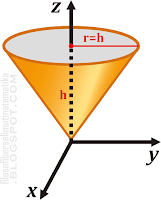
Untuk menentukan momen inersia kerucut di atas, pertama-tama perlu diketahui bahwa kerucut tersebut terbentuk dengan menarik luasan alas (lingkaran) dari z = 0 sampai z = h. Setiap perubahan h jari-jarinya juga berubah dari r = 0 sampai r = h, sehingga dapat dikatakan batas untuk jari-jari tersebut adalah dari r = 0 sampai r = z. Selain itu, kita harus menggunakan sistem koordinat silinder untuk menentukan elemen massanya yang dapat dituliskan
dm = ρ r dr dθ dz
r = r
dengan batas integrasi
r : 0 sampai z
θ : 0 sampai 2π
z : 0 sampai h
sehingga
Demikian penurunan rumus momen inersia untuk berbagai benda, semoga dapat menambah pengetahuan para pembaca dan tidak membingungkan. Jika ada kritik dan saran bisa tinggalkan komentarnya di bawah.Agar pemahamannya lebih lengkap perlu diketahui Materi ini hanya sebagian dari materi fisika dinamika rotasi
dm = ρ dV
dm = ρ r2 sin θ dr dθ dϕ (koordinat bola)
r = r sin θ
dengan batas integrasi
r : 0 sampai R
θ : 0 sampai π
ϕ : 0 sampai 2π
Sehingga
Bola pejal dengan poros di tepi
Momen inersia bola pejal dengan poros di tepi dapat ditentukan dengan teorema sumbu sejajar dengan poros bergeser sejauh R dari poros pusat massanya, sehinggaI = Ipm + md2
I = 2/5 mR2 + m(R)2
I = 2/5 mR2 + mR2
I = 7/5 mR2 (terbukti)
Bola tipis berongga
Momen inersia bola tipis berongga yang dimaksudkan disini adalah sebuah bola yang terlapisi oleh sebuah kulit tipis (seperti bola pingpong), maka dalam menentukan nilai elemen massa (dm) tidak menggunakan volume akan tetapi luas permukaan bola.dm = σ r2 sin θ dθ dϕ dA
r = r sin θ
dengan batas integrasi
θ : 0 sampai π
ϕ : 0 sampai 2π
sehingga
Ekstra TIme
Segitiga
Sebuah segitiga sama sisi yang memiliki panjang sisi sebesar a diputar dengan poros berada pada satu sisi, tampak seperti gambar berikutElemen massa diambil lebar dy dan berjarak y dari sumbu poros. Karena nilai p berubah untuk setiap perubahan y maka, nilai p dapat ditentukan dengan persamaan
dm = σ dA (dA = p dy)
dm = σ p dy
r = y
dengan batas integrasi
y : 0 sampai h
sehingga
Kerucut
Tentukan momen inersia sebuah kerucut yang memiliki tinggi h sama dengan jari-jari alasnya r (h=r) yang diputar dengan sumbu poros z tampak seperti gambar berikutr = r
dengan batas integrasi
r : 0 sampai z
θ : 0 sampai 2π
z : 0 sampai h
sehingga
Demikian penurunan rumus momen inersia untuk berbagai benda, semoga dapat menambah pengetahuan para pembaca dan tidak membingungkan. Jika ada kritik dan saran bisa tinggalkan komentarnya di bawah.Agar pemahamannya lebih lengkap perlu diketahui Materi ini hanya sebagian dari materi fisika dinamika rotasi